为了准确讨论变压器理论,我们必须考虑与变压器相关的一些损耗。一般来说,这些损耗可分为两类:磁损耗或磁芯损耗和 I 2 R 损耗或线圈损耗。磁芯损耗相对恒定,这是因为磁路不会随着变压器电流的变化而发生太大变化。电流会导致 I 2 R 或线圈损耗,并且由于电流发生变化,线圈损耗也会发生变化。
与变压器铁芯相关的所有损耗本质上都是磁性的并且相对恒定。磁滞和涡流的影响不会因为电流的流动而发生太大变化;它们源自材料和设计。
变压器 就像任何电路或设备一样。当电流流动时,它总是会产生磁场和热量。变压器中电流产生的热量称为线圈或铜损耗。计算该损耗的公式与瓦数的公式相同:I 2 R。
关于线圈损耗,需要记住的重要一点是,线圈损耗量与流经变压器的电流直接相关 ,并表现为热量。为了减少这种热损失,变压器线圈可以用铜导体缠绕,铜导体的电阻比相同尺寸的铝导体小。
执行两项测试(开路和短路)以确定变压器中的铁损和铜损。这些损耗进一步用于计算变压器的效率。
效率=输出功率输入功率×100=输出功率输出+Σ(损耗)×100
效率=输出功率输出功率+损耗+铜损耗×100
图1(a)所示为变压器开路测试电路。将交流输入电压设置为变压器的正常初级电平,并在电压表上监测开路输出端子处的电压,如图所示。瓦特表测量输入功率,电流表测量初级电流。由于次级开路,初级电流非常小,电流表和瓦特表上的电压降可以忽略不计。此时,输入电压可作为变压器的初级电压;因此,电压表读数的比率给出了匝数比。
EPES=NPNS
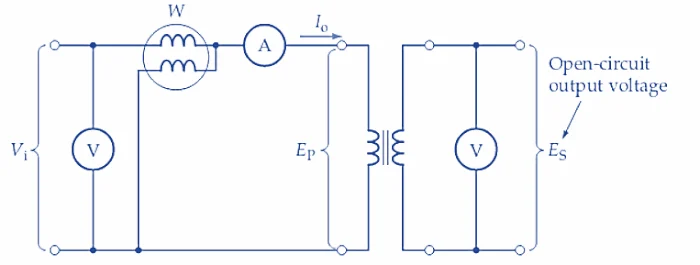
如果初级电流非常小,次级电流接近于零(即电压表电流),则可以假定绕组中的铜损可以忽略不计。瓦特表上测得的输入功率即为变压器铁芯总损耗,电流表则显示空载初级电流 (I o )(见图 1(b))。根据输入电压、电流和功率的测量值,可以确定空载等效电路的组成部分。
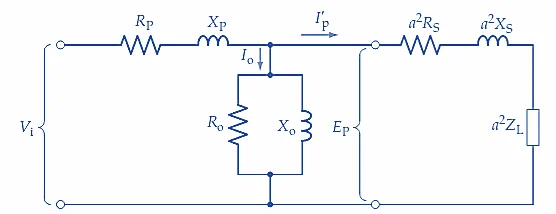
真正的力量,
P=E2PRo
或者
Ro=E2PP
视在功率,
S=EPIo
和
S=√(真实功率)2+(无功功率)2=√P2+Q2
给予
Q=√S2?P2
Q=√(EPIo)2?P2
无功功率可由下式确定:
Q=E2PXo
所以
Xo=E2PQ
实施例1
变压器开路测试产生以下测量结果:E P = 115 V,E S = 57.5 V,P = 9.5 W,I o = 180 mA。确定变压器匝数比以及Ro 和 X o的值。
解决方案
NSNP=ESEP=57.5V115V=12
根据公式 1,
\[R_{o}=\frac{E^{2}_{P}}{P}=\frac{(115\,V)^{2}}{9.5\,W}=1.39k\Omega\ ]
根据公式 2,
Q=√(EPIo)2?P2=√(115V×180mA)2?(9.5W)2==18.39vars
根据公式 3,
Xo=E2PQ=(115V)218.39vars=719Ω
变压器 短路试验是在二次端子短路的情况下进行的,如图2(a)所示。请注意,初级电压 (E P ) 是在变压器初级端子处测量的,以避免由于电流表和瓦特表上的压降而产生误差。输入电压从零开始增加,直到初级电路中的电流表指示正常的满载初级电流。当这种情况发生时,正常的满载次级电流在次级绕组中循环。由于次级端子短路,产生满载初级和次级电流所需的输入电压约为正常输入电压水平的 3%。在如此低的输入电压水平下,磁芯损耗非常小,可以忽略不计。然而,绕组承载正常的满载电流,因此输入提供正常的满载铜损。
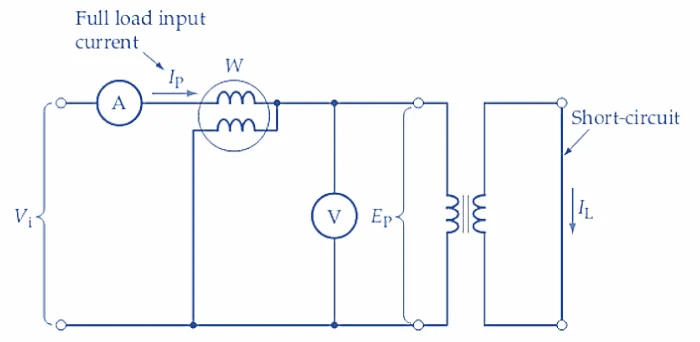
输出功率(到短路)为零,因此测量真实输入功率的瓦特表指示满载铜损。电流表和电压表读数的乘积给出了视在输入功率。根据这些量,可以计算涉及初级的满载等效电路的电阻和电抗分量(见图 2(b))。
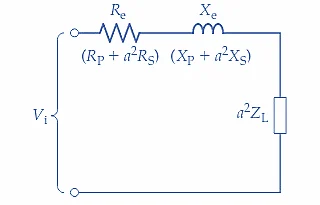
真正的力量
P=I2PRe
Re=PI2P
视在功率,
S=EPIP
无功功率,
Q=√(EPIP)2?P2
无功功率可由下式确定:
Q=I2PXe
所以
Xe=QI2P
实施例2
当在短路测试中进行以下测量时,确定示例 1 中变压器的 Re和 X e :E P(SC) = 5.5 V,I P = 1 A,P = 5.25 W。
解决方案
根据公式 4,
Re=PI2P=5.25W(1A)2=5.25Ω
根据公式 5,
Q=√(EPIP)2?P2=√(5.5V×1A)2?(5.25W)2=1.64var
根据公式 6,
Xe=QI2P=1.64var(1A)2=1.64Ω
变压器的性能通过其电压调整率和效率来描述,并且可以通过开路测试和短路测试这两项测试的结果来预测。开路测试是通过测量(空载)次级电压、初级电流以及输入电压和功率来完成的。为了进行短路测试,将次级侧短路,并将初级电流调整至正常满载水平。测量初级电压和输入功率。
免责声明: 凡注明来源本网的所有作品,均为本网合法拥有版权或有权使用的作品,欢迎转载,注明出处。非本网作品均来自互联网,转载目的在于传递更多信息,并不代表本网赞同其观点和对其真实性负责。