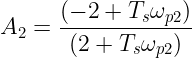用于模拟 III 型补偿器的数字等效
标准 III 型补偿器的电路图如图 1 所示。
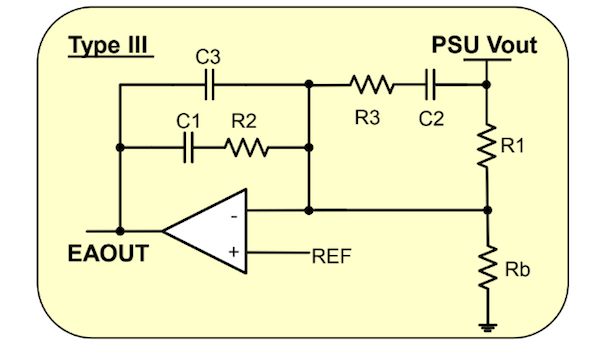
图 1：模拟 III 型补偿器
从 Biricha 的设计研讨会 [1,3] 和之前的文章 [2]，我们知道该补偿器有 3 个极点和 2 个零点，如下面的传递函数 Hc(s) 所示：
我们可以看到，原点处有一个极点，还有两个极点和两个零点。再次从 Biricha 的研讨会和博多之前的文章中，我们确切地知道如何在模拟世界中放置这些极点和零点，以获得具有所需交叉频率和相位裕度的稳定环路。请注意，所有项均以弧度为单位，所有 F 项均以 Hz 为单位。
该电路的数字等效 LDE 如下所示：
左 [ n-3 \右
请不要让冗长的方程式让您望而却步；我们很快就会解释一切。这称为3 极 3 零数字补偿器 (3p3z)，每次在模拟世界中我们在数字中使用 III 型时，我们都必须使用 3p3z 才能获得近乎的性能。请注意，与模拟相比，数字中我们有一个额外的零。
从模拟世界到数字世界的转变
这只是我们从模拟世界向数字世界转换的产物，因此，该方程在频域中的数值输出几乎是图 1 中模拟运算放大器的复制品。就像运算图一样对于上一篇文章的积分器，我们现在忽略所有缩放和时间延迟的影响。
从上一篇文章中我们知道，上面等式中的 y[n] 是我们在该具体实例中数字补偿器的输出，即在该具体时刻的需求 PWM 的新值。我们还知道 x[n] 是在这个确切实例中我们对数字补偿器的输入，即在这个确切时刻的误差信号。对于电源，这通常是 ADC 采样的实际输出电压与需求/参考电压之间的差异。
我们还知道 y[n-1] 表示我们之前的输出，即来自一个采样间隔的输出。如果我们假设开关/采样频率为 200kHz，则每个采样间隔将为 5us。因此“前一个输出”就是补偿器5us前的输出。
类似地，y[n-2] 将是 10us 前的“前一个前一个输出”，例如 x[n-3] 将是 15us 前的“前一个前一个输入”，依此类推。，您可以看到 y 项乘以一组系数：A1、A2、A3，x 项乘以另一组系数 B0、B1、B2、B3。
这些系数决定了极点和零点的位置。现在忽略所有缩放比例和时间延迟，如果我们知道模拟补偿器的极点和零点位置（我们确实这样做），那么要创建等效的数字补偿器，我们所要做的就是使用以下方程计算这 7 个系数：
正确的 ）
正确的 ）
欧米伽 _{p2})(2+T_{s}\欧米伽
欧米茄
我很欣赏这些转换方程乍一看可能看起来很大而且令人生畏，但好消息是这些方程中没有任何我们不知道的东西。我们现在将通过一个现实生活中的数值示例来证明这一点。
假设我们为 200kHz降压转换器设计了一个模拟 III 型补偿器，其具有以下极点和零点：
其中 Fz1 和 Fz2 是我们的零点，Fp1 和 Fp2 是补偿器极点，Fp0 是我们的原点极点。
系数(A1)计算
现在让我们根据上面的方程计算个系数 (A1)。是的，我知道这是一个很长的方程，但请看一下这个方程中是否有我们不知道的东西。我们什么都知道！
是我们的采样间隔，在我们的例子中，200kHz 开关频率为 5us，并且 是我们在模拟世界中的补偿器极点，我们知道 Fp2 = 6576.65 kHz，Fp3 = 100 kHz（不要忘记转换为弧度）。
因此，我们可以准确计算出A1为1.590703155656。现在请看一下其他令人生畏的系数方程。与 A1 方程一样，尽管这些方程很长，但其中没有我们不知道的内容，因此我们可以轻松计算所有方程。将我们的模拟极点和零点代入上述方程并将 Ts 设置为 5us，我们有：
（-0.180452115956）
新的 PWM 占空比
您现在可以看到我们有一个简单的 LDE，类似于上一篇文章中我们之前的简单运算放大器补偿器的 LDE，因此我们可以轻松地让 MCU 来计算它。提醒一下，我们的输出 y[n] 是新的 PWM 占空比，输入 x[n] 是需求输出电压与 ADC 实际测量的输出电压之间的差值：
我们的设计已完成，该方程的表现应与具有上述极点和零点的模拟 III 型补偿器几乎完全相同。
模拟 II 型的数字等效
补偿器 标准 II 型补偿器的电路图如图 2 所示。
图 2：模拟 II 型补偿器
您可以看到，Type II 和 Type III 之间的区别是 Type III 电路中省略了 R3 和 C2。所有这意味着我们的 II 型传递函数少了一个极点和一个零，如下所示：
数字世界中 II 型的线性差分方程有 2 个极点和 2 个零点，因此称为 2 极点 2 零 (2p2z) 控制器。
在模拟世界中的任何时候，我们都使用 II 型，在数字世界中，我们可以使用
我们的 2p2z LDE 只有 5 个系数（3p3z 有 7 个系数）。这些内容如下：
同样，即使方程很长，您也可以看到，只要我们有模拟世界中的极点和零点以及采样间隔 Ts，就没有未知数，我们可以计算一切。
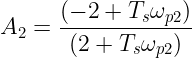
缩放和时间延迟的影响
我们导出的 LDE 是运算放大器传递函数的数字等效项，但数字电源内会有各种元件为增益图添加恒定的比例因子。
例如，如果我们电源的输出为 6.6V，而我们对其进行采样的 ADC 只能承受 3.3V，那么我们就添加了一个“除以二”分压器。我们的增益波德图需要考虑 0.5 的比例因子，因此我们的交叉频率将偏离 0.5 倍。类似地，所有纯时间延迟（例如，从我们使用 ADC 采样输出电压的时间到我们更新 PWM 的时间）所花费的时间，都会在相位图中添加相位延迟。因此，我们终得到的相位裕度将低于我们的预期。
到目前为止，我们忽略了各种缩放和时间延迟的影响。好消息是，所有这些都很容易计算，我们将在下一篇文章中介绍它们。我们还将提供分步设计并用完整的实验结果进行验证。
