TCCS 配置

　　图 1 显示了 TCCS 放大器的原理图。

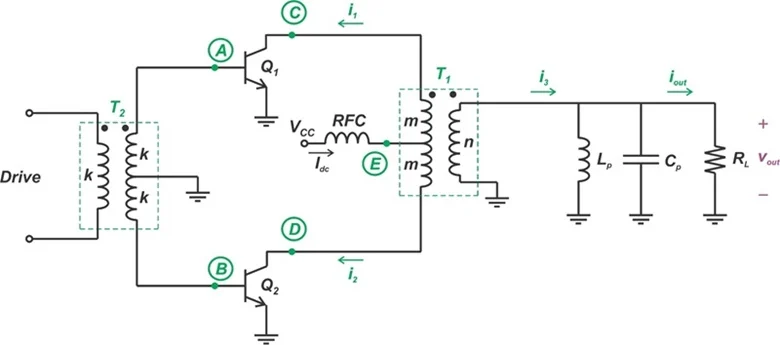
　　变压器耦合电流开关 D 类放大器的示意图。
　　图 1.变压器耦合电流开关 D 类放大器。

　　图 2 重现了上一篇文章中的 TCVS 原理图。让我们简单回顾一下这两个放大器之间的异同。

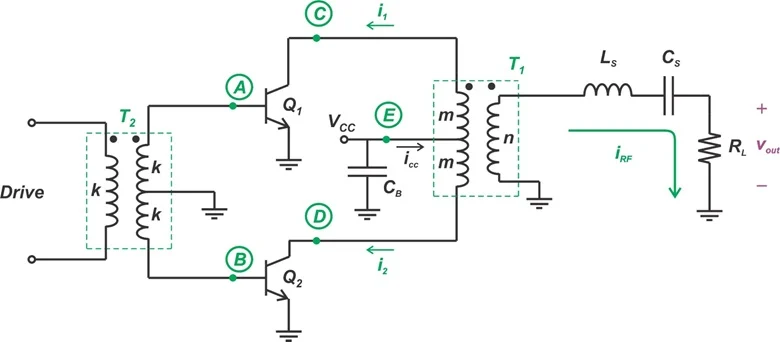
　　变压器耦合电压开关 D 类放大器的示意图。
　　图 2.变压器耦合电压开关 (TCVS) D 类放大器。
　　我们先从相似之处开始。两个放大器都使用中心抽头输入变压器 (T 2 ) 从输入信号产生反极性信号。T 2的中心抽头接地；T 2次级的反极性信号用于驱动两个晶体管 (Q 1和 Q 2 )，使其足够强，以使其充当开关。Q 1和 Q 2在输入信号的交替半周期内工作。
　　两种电路还使用输出变压器 (T 1 ) 来合并集电极电流。然而，在 TCVS 配置中，T 1的中心抽头直接连接到电源 ( V CC )。TCCS 放大器通过 RF 扼流圈 (RFC) 将中心抽头连接到V CC。RF 扼流圈在开关频率下具有无穷大的电抗，可阻止交流电流并迫使恒定电流进入变压器中心抽头。
　　T 1的中心抽头是两种配置之间的两个主要差异之一。第二个差异是负载网络。与使用串联 RLC 电路作为负载的电压切换配置不同，电流切换放大器在输出端具有并联 RLC 网络。
　　TCCS 放大器的运行
　　在工作的每个半周期内，电流 ( Idc ) 被射频扼流圈强制流入输出变压器 (T1) 的中心抽头。然后，电流通过两个开关 (晶体管 Q1 和 Q2) 之一，到达地。

　　图 3 和图 4 中的简化图说明了 TCCS 放大器在两个连续半周期内的运行情况。理想开关 S 1和 S 2分别取代 Q 1和 Q 2。

　　当 Q1 开启且 Q2 关闭时的 TCCS 放大器。
　　图 3.当 S 1闭合且 S 2断开（Q 1开启且 Q 2关闭）时的 TCCS 放大器。

　　当 Q1 处于关闭状态且 Q2 处于打开状态时的 TCCS 放大器。

　　图 4.当 S 1打开且 S 2关闭（Q 1处于关闭状态且 Q 2处于打开状态）时的 TCCS 放大器。
　　在图 3 中，S 1闭合，S 2断开。因此， I dc流过 S 1 ( i 1 = I dc )。由于 S 2断开，因此没有电流可以流过下部路径 ( i 2 = 0)。在下一个半周期（图 4）中，S 1断开，S 2闭合，导致i 1 = 0 和i 2 = I dc。假设在个半周期中 S 1断开，S 2闭合，我们将获得图 5 中的电流波形。

　　两个完整工作周期内集电极电流的波形。

　　图 5.两个完整工作周期内i 1和i 2的电流波形。
　　我们可以看到，集电极电流（i 1和i 2）是方波，在 0 和I dc之间切换。请注意，I dc仍然是一个未知参数——直到分析结束我们才能找到它的值。现在，我们需要确定流过 T 1次级的电流。上图中，该电流用i 3表示。
　　根据半周期，扼流圈输送的电流会流过初级绕组的上半部分或下半部分。因此，由于变压器的作用，次级绕组中电流的幅度为 ( m / n ) Idc。但是，该电流的方向在半周期之间交替。图 6 显示了两个完整工作周期内i3的电流波形。

　　两个工作周期内的次级电流波形。

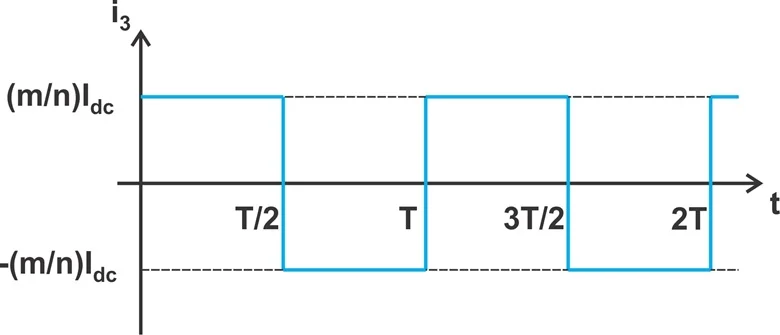
　　图 6.两个工作周期内的次级电流波形。
　　要理解为什么i 3在( m / n ) I dc和 –( m / n ) I dc之间切换，我们需要结合电路图来考虑图 5 的集电极电流波形。在个半周期内，扼流圈输送的电流流过初级绕组的下半部分。由于它进入初级绕组的虚线端，因此次级电流从虚线端流出，从而导致i 3 = ( m / n ) I dc。
　　然而，在下一个半周期中，扼流圈的电流流过初级绕组的上半部分。由于初级电流从该绕组的点端流出，输出电流进入次级绕组的点端。因此，我们有i 3 = –( m / n ) I dc。
　　分析 TCCS 放大器的性能
　　50% 占空比方波包含所有奇次谐波（第 1 次、第 3 次、第 5 次等）。使用傅里叶级数表示法，我们可以用图 6 中的方波电流的组成频率分量来表示：
　　$$i_3~=~\frac{4}{\pi} \frac{m}{n}I_{dc} \sum_{p=1}^{\infty}\frac{\sin((2p~-~1)\omega_{0}t)}{2p~-~1}$$
　　等式 1.
　　电流切换电路将所有这些谐波分量的总和施加到负载网络。但是，调谐到开关频率的高 Q 并联 RLC 电路对除基波分量之外的所有电流频率分量都呈现非常小的阻抗。在基波频率下，RLC 电路呈现R L的电阻。因此，所有输出电流谐波都被短路，只有基波分量流入负载电阻 ( R L )。
　　设流过R L 的电流为i out，则可得：
　　$$i_{out}~=~\frac{4}{\pi} \frac{m}{n}I_{dc} \sin(\omega_0 t)$$
　　等式 2.
　　i out的峰值等于 \(\frac{4}{\pi} \frac{m}{n} I_{dc}\)。i out ( i rms ) 的 RMS 值等于峰值除以 2 的平方根。知道了这一点，我们现在可以计算出输送到负载的平均功率：
　　$$P_{L} ~=~ R_L i_{rms}^2 ~=~ \frac{8}{\pi^2} (\frac{m}{n})^2 {I_{dc}^2}{R_L}$$
　　等式 3.
　　问题在于我们仍然不知道流过电感器的电流I dc。除非我们能知道，否则公式 3 对我们没有用。要找到I dc，我们需要进一步研究电路。
　　计算通过射频扼流圈的电流
　　假设 RF 扼流圈是理想的。由于情况如此，因此它两端没有直流电压降。因此，输出变压器中心抽头处的电压直流分量等于V CC。这条信息对于找到I dc至关重要。
　　为了找到变压器中心抽头的电压波形，我们首先使用公式 2 来确定变压器次级绕组两端的电压：
　　$$v_{out}~=~\frac{4}{\pi} \frac{m}{n}I_{dc} R_L \sin(\omega_0 t)$$
　　等式 4.
　　由于变压器的电压调节功能，因此初级绕组各段两端的电压为：
　　$$v_{p}~=~\frac{4}{\pi} (\frac{m}{n})^2 I_{dc} R_L \sin(\omega_0 t)$$
　　等式 5.
　　图 7 提供了个半周期（Q 1：关闭，Q 2：开启）的电路简化图。相关电压量（v out和v p）以紫色显示。
　　Q1 关闭且 Q2 开启时的电压。
　　图 7. Q 1关闭且 Q 2导通时的电压。
　　考虑上图中的节点 C、D 和 E。节点 C 和 D 分别位于 Q 1和 Q 2的集电极。节点 E 出现在 T 1的中心抽头处。在此半周期中，节点电压如下：
　　vC = 2vp
　　VD = 0
　　vE = vp
　　请注意，节点 E 和 C 具有正弦电压。
　　图 8 显示下一个半周期（Q 1：开启且 Q 2：关闭）。
　　Q1 开启且 Q2 关闭时的电压。
　　图 8. Q 1开启且 Q 2关闭时的电压。
　　对于这个半周期，节点电压为：
　　VC = 0
　　vD = -2vp
　　vE = – vp
　　在此半周期内，节点 E 和 D 处的电压为正弦波。然而，它们相对于v p和v out是反转的。
　　图 9 显示了这些节点的电压波形以及输出在一个完整操作周期内的情况。
　　从上到下：输出端、节点 D、节点 C 和节点 E 的电压波形。
　　图 9. 从上到下：输出、节点 D、节点 C 和节点 E 处的电压波形。
　　在上图中，A 1和A 2分别是v out和v E的幅度。A  1只是公式 4 中v out的峰值：
　　$$A_{1}~=~\frac{4}{\pi} \frac{m}{n}I_{dc} R_L$$
　　等式 6.
　　根据半周期，v E等于v p或 – v p 。根据公式 5 取v p的峰值，我们得到：
　　$$A_{2}~=~ \frac{4}{\pi} (\frac{m}{n})^2 I_{dc} R_L$$
　　等式 7.
　　幅值为A 2 的全波整流正弦波具有 2 A 2 /π的直流分量。因此， v E的平均分量为：
　　$$v_{E, \ ave} ~=~ \frac{2}{\pi} ~\times~ \Big ( \frac{4}{\pi} (\frac{m}{n})^2 I_{dc} R_L \Big ) ~=~ \frac{8}{\pi^2} (\frac{m}{n})^2 I_{dc} R_L$$
　　等式 8.
　　我们之前提到过，输出变压器中心抽头（节点 E）处电压的平均分量是V CC。在上述公式中，用V CC代替v E, ave ，我们可以解得I dc：
　　$$I_{dc} ~=~ \frac{\pi^2}{8} (\frac{n}{m})^2 \frac{V_{CC}}{R_L}$$
　　等式 9.
　　，将公式 9 中的I dc代入公式 3 中，我们得到输出功率：
　　$$P_{L} ~=~ \frac{\pi^2}{8} (\frac{n}{m})^2 \frac{V_{CC}^2}{R_L}$$
　　等式 10。
　　现在我们知道了I dc，我们也可以找到一个简单的公式来计算集电极的电压。在图 9 中，我们看到v C和v D（两个集电极电压）都具有峰值 2 A 2。将公式 9 和公式 7 结合起来可得出：
　　$$A_{2}~=~ \frac{\pi}{2} V_{CC}$$
　　等式 11.
　　晶体管两端的电压降为 2 A 2 = π V CC。
　　现在我们准备计算 TCCS 放大器的效率。这是我们继续之前要检查的一个性能参数。
　　计算效率
　　效率是通过比较输出功率和输入功率来计算的。我们从公式 10 知道输出功率。至于输入功率，它等于电源电压 ( V CC ) 乘以电源电流的平均值 ( I dc )。因此，从公式 9 可得出输入功率为：
　　$$P_{CC} ~=~ V_{CC} I_{dc} ~=~ \frac{\pi^2}{8} (\frac{n}{m})^2 \frac{V_{CC}^2}{R_L}$$
　　等式 12.
　　这与传送到负载的功率相同，这意味着该放大器的理论效率为 100%。请注意，这是理想效率。实际上，电路的效率可能会因非理想因素（例如与集电极引线串联的寄生电感）而降低。