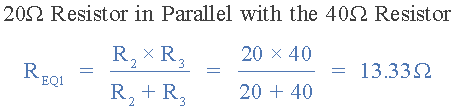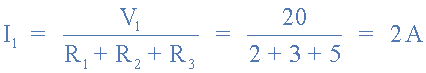叠加定理是另一种电路分析工具，我们可以用它来查找线性电路周围的电压和电流。如果电路包含一个或多个独立的电压和/或电流源，我们可以使用叠加定理来找出每个单独源的电压和/或电流贡献，然后将它们代数相加，以找到电路周围任何一点的实际电压和/或电流值。
　　也就是说，我们可以使用叠加定理将电路周围的电压和电流叠加或代数相加，因为每个独立源单独作用会获得特定电路元件或节点上的总电压或流过该电路元件或节点的总电流。
　　使用叠加定理代替以前的网格分析或节点分析的优点是数学变得更容易，因为我们不需要使用行列式、联立方程或矩阵代数来分析给定的电路。然后，叠加是我们用来分析可能包含许多不同有源源的直流和交流电路的便捷工具。
　　然而，叠加定理的缺点是它只适用于线性电路。幸运的是，电阻( R )、电感( L ) 和电容( C )等无源元件的v、i关系都是线性的。
　　与之前的电路分析技术（基尔霍夫定律、戴维南定律、诺顿定律等）一样，我们必须“关闭”电路周围的所有电源，只留下一个理想电压源或一个理想电流源进行电路分析。这很容易做到，只需开路所有电流源并短路所有电压源，即可找出特定电压或电流源对电路的影响。
　　也就是说，如果用短路代替电压源，则可以有效地将 it 归零，因为短路两端的电压降为零伏，即v = 0。而如果用开路代替电流源，则可以有效地将 it 归零，即 ( i = 0 )，因为没有电流可以流过开路（假设是理想电源）。
　　请注意，相关源不显示固定的电压或电流值，而是由电路中的其他电流或电压或外部源控制，因此不能关闭或停用。

　　让我们首先考虑前面教程中的 T 型直流电路。

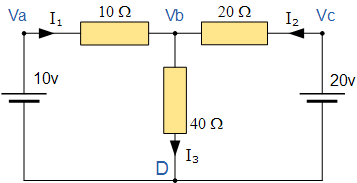
　　叠加定理电路
　　这里，我们需要找到流过中心 40Ω 电阻R 3的电流，也就是I 3。

　　只要我们在整个电路分析过程中保持一致，顺时针或逆时针分析电路对终结果没有影响。然后，首先，我们将用短路替换 20 伏电池，这样 10V 电池就单独作用于电路，如下所示。

　　叠加电路

　　可以看出，将电压源V 2短路至地，右侧20Ω电阻现在实际上与中心40Ω电阻并联。然后作为两个并联电阻，它们的等效并联电阻计算如下：

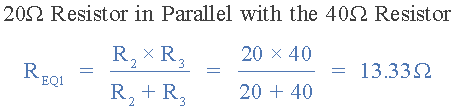
　　并联电阻方程

　　左侧的10Ω电阻R 1与13.33Ω的等效并联电阻R EQ1串联，使得电流I 1流过的串联电路总电阻为 (10 + 13.33) = 23.33Ω 。

　　利用分压器规则，我们可以找到由于 10V 电池供电而在节点A处的电压。

　　节点A处的叠加电压
　　查找电流 I R3(1)
　　流过40Ω电阻R3的电流由 10 伏电池电源V 1驱动，其计算公式如下：
　　IR3 (1) = V A /R 3 = 5.71/40 = 0.143A，或143mA
　　因此，由于 10V 电池电压V 1单独作用于电路，流过电阻R 3 的电流为143mA。
　　如果愿意的话，我们可以再检查一下这个值，因为在节点A 的5.71 伏电压V A上有两个并联的电阻支路，分别为40Ω和20Ω：
　　I 1 = 10/23.33 = 0.429A，且IR2 = 5.71/20 = 0.286A
　　因此：I R3(1) = I 1 – I R2 = 0.429 – 0.286 = 0.143A，或 143mA（正确）
　　查找电流，I R3(2)

　　使用与之前相同的方法和计算逻辑，我们现在可以计算出流过电阻R 3 的电流，该电流由 20 伏电池电压V 2驱动。

　　第二叠加电路

　　10 伏电池V 1被短路替换，因此 20 伏电池V 2在电路中单独起作用。同样，有两个并联电阻支路R 1和R 3，它们的等效并联电阻计算如下：

　　等效电阻方程
　　现在，右侧的20Ω电阻R 2与8Ω的等效并联电阻R EQ2串联，使得电流I 2流过的总串联电阻为 (20 + 8) = 28Ω 。

　　再次，利用分压器规则，我们可以根据V 2找到节点A处的电压。

　　计算叠加电压
　　纯属巧合，节点A处的 5.71 伏电压对于两个电压源在每个方向上的作用都是相同的值。然后，流过40Ω电阻R 3 的电流由 20 伏电池源驱动，V 2再次计算为：
　　IR3 (2) = V A /R 3 = 5.71/40 = 0.143A，或143mA
　　现在，为了找到I R3的终值和方向，我们只需找到两个计算电流I R3(1)和I R3(2)的代数和，其公式如下：
　　I R3的大小和方向
　　I R3 = I R3(1) + I R3(2) = 0.143 + 0.143 = 0.286，即286mA
　　再次，这与我们在先前的电路分析教程中使用基尔霍夫电路定律、戴维南定理和诺顿定理得出的数值 0.286 安培相同。
　　当两个电压源重新连接到电路时，我们可以使用欧姆定律计算节点A处的电压，从而计算R 3上的电压降。根据欧姆定律， V R3 = I R3 x R 3 = 0.286 x 40 = 11.44伏。这与之前的电路分析教程中找到的值相同。
　　然后我们在这里看到，叠加定理可用于简化具有两个或多个电压/电流源的任何线性网络的分析所涉及的数学运算。该定理也可应用于任何同时包含直流和交流源的网络。
　　但请注意，叠加定理不适用于功率，因为??电功率是非线性量，它与电流的平方 ( I 2 *R ) 成正比，与电压的平方 ( V 2 /R ) 成反比。
　　叠加定理例子2
　　现在让我们引入一个电流源，并使用叠加定理来找到以下电路中2Ω电阻器R 1两端的电压降。

　　叠加电路

　　叠加定理电路示例二

　　再次分析电路，我们必须短路电压源，开路电流源，以便任何时候只留下一个电动势源为电路供电。然后，首先，我们将开路 8A 电流源，并使用 20V 电压源分析电路，如图所示。

　　开路电流源

　　我们可以清楚地看到，现在的电路类似于跨接在V 1上的串联电阻电路。基尔霍夫电压定律 (KVL) 给出V 1为：I 1 (R 1 + R 2 + R 3 )，我们可以使用欧姆定律找到流过该串联电路的电流I 1 。

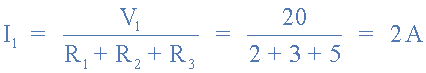
　　串联叠加电路电流
　　因此，如果串联电路中流过的电流为 2 安培，则电阻器R 1两端的电压降计算如下：
　　V R1(1) = I 1 x R 1 = 2 x 2 = 4伏
　　因此，由于 20 伏电池供电，电阻器 R 1两端的电压降为 4 伏。如果愿意，我们还可以使用分压器规则来查找环路其余部分的剩余电压降。
　　如果V 1现在短路（电压源），并且 8 安培电流源重新连接到电路中。电路现在类似于：
　　并联电路分流器
　　现在我们可以看到，我们在 8 安培电流源上并联了电阻，形成了通常所说的分流电路。电流源施加到两个并联支路。一个支路包含串联的电阻器R 1和R 2，另一个支路包含单独的电阻器R 3 。
　　基尔霍夫电流定律 (KCL) 告诉我们，电路中的总电流等于所有并联支路电流的总和。即：IT = 8A = I1 + I2，由于我们想知道电阻器R1两端的压降，因此我们需要找到流过该并联支路的电流。
　　分流器规则规定，流过一条支路的电流等于总电流乘以总电流比。然后，流过并联支路R 1和R 2 的电流计算如下：
　　并联支路电流
　　由于有 4 安培的电流流过电阻器R 1和R 2的左并联支路，我们可以使用欧姆定律找到R 1两端的电压降，如下所示。
　　V R1(2) = I 1 x R 1 = 4 x 2 = 8伏
　　请注意，如果每个并联支路的电阻值相同（如本例所示），电流将在每个支路之间均等分配。如果电阻值不同，则流过电阻值的支路的电流较少，反之亦然。
　　因此，当 8A 电流源和 20V 电??压源重新连接到电路时，电阻器R 1两端的实际电压为：
　　V R1 = V R1(1) + V R1(2) = 4V + 8V = 12 伏
　　同样，我们可以使用相同的分析技术来找到电阻器R 2和R 3两端的电压降。
　　叠加定理总结
　　我们在这里看到，在任何包含几个独立电压或电流源的线性电路中，我们可以使用叠加定理来找到由这些独立源单独作用产生的跨越每个电路元件的电压和/或流过每个电路元件的电流，然后结合它们对电路的影响。
　　为了使叠加定理准确发挥作用，所有理想电压源都应由短路代替，所有理想电流源都应由开路代替。请注意，非理想源通常由其内部电阻代替。
　　然后，使用叠加定理解决任何电路的基本步骤如下：
　　1.确定电路中所有独立源，例如电压源和电流源，并在电路中仅选择一个源。
　　2.关闭（短路或开路）所有其他独立源，仅使用一个活动源分析电路。
　　3.使用标准电路分析技术（欧姆定律、基尔霍夫定律）确定由于单个选定源而产生的跨电路元件、分支或节点的电压或流过该电路元件、分支或节点的电流。
　　4.对每个独立源重复上述操作，每次一个，只考虑该源的影响，同时保持所有其他源关闭。
　　5.用代数方法求和从每个源获得的单独响应，以找到感兴趣的电路元件、分支或节点的总响应。
　　6.当所有源同时作用时，要注意极性、符号约定和组合响应的流向。