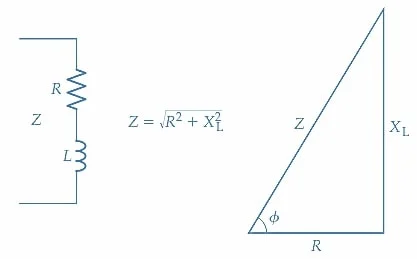在串联 RL 电路中，电阻器和电感器以串联配置连接，这意味着流过电路的电流依次通过两个元件。电路中的电感器产生磁场，以电磁场的形式存储能量。另一方面，电阻器阻碍电流流动并耗散电路中存储的能量。
　　图 1(a) 显示了由电感 (L) 和电阻(R) 组成的串联电路 ，图 1(b) 和 (c) 分别显示了该电路的波形和相量图。参考电路图，可以看出（对于所有串联电路）电流 I 是 R 和 L 共同的，因此电路波形从电流波形开始绘制。

　　电阻两端的电压 (V R ) 始终与流过电阻的电流同相。因此， 图 1(b) 中V R的波形与电流波形同相。电感电压 (V L ) 比流过电感的电流超前 90°。因此，图 1(b) 中 V L的波形 比 I 超前 90°。施加的电压 E 是两个分量电压 V R 和 V L的合力，其波形只需将 V R 和 V L的瞬时电平相加即可获得。E 比 I 超前一个小于 90° 的角度 (φ)。

　　（a）串联 RL 电路

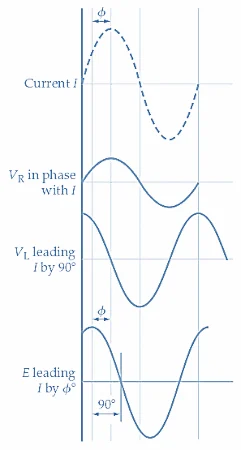
　　（b）电路波形

　　（c）相量图
　　图 1. 在串联 RL 电路中，电流滞后电感电压 (V L ) 90°，滞后电源电压 (E) 小于 90°。图片由 Amna Ahmad 提供
　　相量图
　　绘制串联 RL 电路的相量图首先要绘制电流相量，因为电流是串联电路中的常见量。按比例绘制一条水平线表示电流 I [图 1(c)]。由于 V R 与 I 同相，因此在 I 旁边绘制另一条水平线表示 V R。电感电压 (V L ) 比 I 超前 90°；因此，V L的相量 垂直绘制，与 I 成 90° 角。V L 和 V R的相量相加得出 的结果表示施加的电压 (E)。再次可以看出，施加的电压超前电路电流一个角度 φ，该角度小于纯电感电路中 E 和 I 之间的 90° 角。
　　电路方程
　　E 可以用直角坐标或极坐标形式表示。参考图 1(c)
　　\[E=V_{R}+jV_{L}\,\,\,(1)\]
　　或者以极坐标形式
　　\[E=\sqrt{V^{2}_{R}+V^{2}_{L}}\angle\Big(\frac{V_{L}}{V_{R}}\Big)\,\,\,(2)\]
　　将公式 1 除以 I 可得出
　　\[\frac{E}{I}=\frac{V_{R}}{I}+j\frac{V_{L}}{I}\]
　　V R /I 是电阻两端的电压除以流过电阻的电流。因此，V R /I 可以用 R 代替。此外，V L /I 是电感电压除以流过电感的电流，后者可以用感抗 X L代替。E/I 既不是电阻也不是感抗，因为它同时包含这两个组成部分。在这种情况下，E/I 称为阻抗，符号为 Z。因此，如图 2 所示，上述等式可以重新表述。
　　阻抗
　　\[Z=R+jX_{L}\,\,\,(3)\]
　　当R和X L 以欧姆表示时，Z的单位也是欧姆。Z的数值或模数（即不包括角度）写为Z。
　　所以
　　\[|Z|=\sqrt{R^{2}+X^{2}_{L}}\,\,\,(4)\]
　　Z 的相位角为
　　\[\Phi=\Big(\frac{X_{L}}{R}\Big)\,\,\,(5)\]
　　结合公式 4 和公式 5
　　\[E=\sqrt{R^{2}+X^{2}_{L}}\angle\Big(\frac{X_{L}}{R}\Big)\,\,\,(6)\]

　　公式 6 表示从矩形形式（Z=R +jX）到极坐标形式（Z∠）的转换。

　　图 2. 电感器和电阻器串联组成的电路的阻抗为 (Z = R + jX L )。图片由 Amna Ahmad 提供
　　阻抗图

　　Z、R 和 X L这些量 可以用矢量图表示。它们不是相量，因为它们具有固定值。与交流电压和电流量不同，Z、R 和 X L 没有连续变化的瞬时值。为了将阻抗、电抗和电阻的矢量图与相量图区分开来，它通常以三角形形式绘制，并称为阻抗图。图 3 显示了图 1(a) 中串联 RL 电路的阻抗图。首先绘制一条水平线来表示电阻分量 R。然后相对于 R 以 +90° 绘制 +j 分量 (X L )，如图所示。Z 分量是三角形的斜边，角度 φ 是阻抗 Z 相对于电阻 R 的相位角。

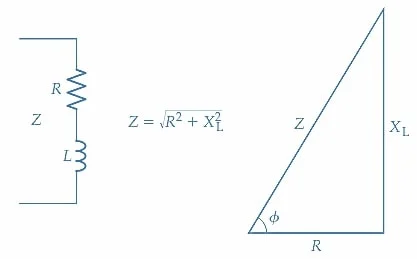
　　图 3. 串联 RL 电路的阻抗图（或阻抗三角形）。电感电抗矢量 X L 与电阻矢量成 90° 角（向上）。阻抗 (Z∠?) 是 R 和 X L的结果。图片由 Amna Ahmad 友情提供
　　准入
　　阻抗的倒数与电导（电阻的倒数）和电纳（电抗的倒数）一样，也是电路分析中一个非常重要的量。导纳（符号 Y）是阻抗（Z）的倒数，其单位是西门子（S）。
　　准入
　　\[Y=\frac{1}{Z}\,\,\,(7)\]
　　当公式 7 中 Z 以欧姆为单位时，Y 以西门子为单位。
　　实用电感器
　　所有电感器都是具有一定绕线电阻的线圈，并且如前所述，实际电感器可以用与绕线电阻串联的纯电感来表示。因此，图 1 和图 3 中的图表可适用于电感器直接连接到交流电源的情况。当外部电阻与电感器串联时，绕线电阻也应在等效电路中显示为串联元件。
　　串联 RL 电路分析
　　计算感抗 X L  = 2πfL
　　如果有多个电阻元件，则计算总电阻：
　　R = R 1  + R 2  + …
　　计算电路阻抗
　　\[|Z|=\sqrt{R^{2}+X^{2}_{L}}\]
　　计算相位角φ=XLR
　　计算电流 I = E/Z
　　确定电阻电压 V R = IR 或 V R  = E cos ?
　　确定感应电压 V L  = IX L 或 V L = E sin ?
　　示例 1
　　分析图 4 中的串联 RL 电路，确定电流、R 两端的电压、L 两端的电压以及电流相对于电源电压的相位角。
　　解决方案
　　电感电抗
　　\[X_{L}=2\pi fL=2\pi\times100Hz\times20mH\approx12.5\Omega\]
　　电路阻抗
　　\[|Z|=\sqrt{R^{2}+X^{2}_{L}}=\sqrt{(20\Omega)^{2}+(12.57\Omega)^{2}=23.6\Omega}\]
　　相位角
　　\[\Phi=\Big(\frac{X_{L}}{R}\Big)=\Big(\frac{12.56\Omega}{20\Omega}\Big)=32.1\degree\]
　　电路电流
　　\[I=\frac{E}{Z}=\frac{60V}{23.6\Omega\angle32.1\degree}\approx2.54A\angle-32.1\degree\]
　　参考图 1(c) 串联 RL 电路相量图：
　　电阻电压
　　\[V_{R}=Ecos\Phi=60Vcos32.1\degree=50.8V(=I\times R)\]
　　电感电压

　　\[V_{L}=Esin\Phi=60Vcos32.1\degree=31.9V(=I\times X_{L})\]

　　图 4. 示例 1 的串联 RL 电路。图片由 Amna Ahmad 提供
　　串联 RL 电路行为要点
　　串联 RL 电路是一种重要的电路，由 与电源串联的电阻器和电感器组成。串联 RL 电路的行为可以用阻抗图和相量图来描述，它们以图形方式表示电压和电流之间的复阻抗和相位关系。阻抗图将电路的阻抗表示为复平面中的矢量，而相量图将电压和电流之间的相位关系表示为旋转矢量。理解这些图对于分析和设计串联 RL 电路以及理解电路中无功元件的行为至关重要。