在运算放大器上仅包含一个电容器或电感器和 3 个电阻器的简单带通 RC 和 LR 滤波器方案。对所提出的滤波器的幅频特性以及 Robert Allen Pease 的 RC 滤波器及其改进的 LR 变体进行了比较。
　　在整套简单的低频滤波器中，可以突出 Sallen-Key 滤波器 [1, 2]。尽管这些滤波器外观简单，但设置起来却非常困难，需要使用协调部件。
　　RC 滤波器由乔治·A·菲尔布里克研究公司的工程师罗伯特·皮斯（Robert Pease）于 1971 年提出（图 1 [3, 4]），具有几个独特的特性。它非常简单，其谐振频率仅由一个电位器 R2 控制，滤波器的传输系数几乎不依赖于该电位器的电阻值。调节电位器 R2 时，该滤波器的幅频特性如图 1 [5] 所示。
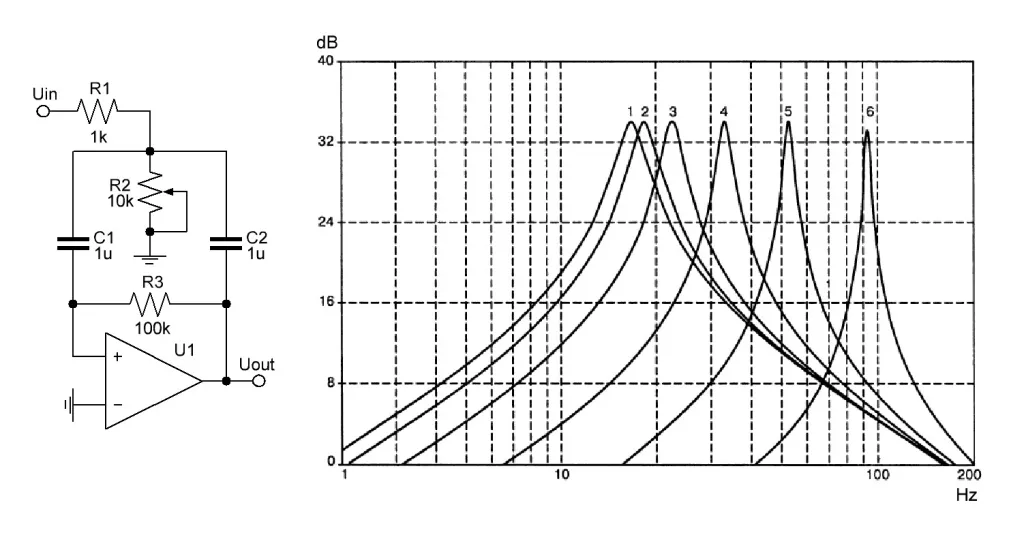
　　图 1 Pease RC 滤波器电气图及其幅频特性，其中 R2 为：1) 10.0 kΩ；2) 3.0 kΩ；3) 1.0 kΩ；4) 0.3 kΩ；5) 0.1 kΩ；6) 0.03 kΩ。

　　对Pease电路稍加修改，即用电感代替电容，得到改进的滤波电路。改进的LR滤波器在R2电位器调整过程中的幅频特性如图2 [ 5]所示。

　　图 2改进型LR滤波器的电气图及其幅频特性，其中R2为：1）0.03 kΩ；2）0.1 kΩ；3）0.3 kΩ；4）1.0 kΩ；5）3.0 kΩ；6）10.0 kΩ。L1=L2=20 mH。

　　除了运算放大器之外，上述滤波器每个都包含 5 个元件。但是，可以提供更简单的滤波器，仅包含 4 个元件，其中元件 R3 + R4 可以用一个电位器代替。

　　图 3中 RC 滤波器的“谐振”频率由以下表达式确定：
　　其中f 0单位为 Hz，R 单位为 Ω，C 单位为 F，a是取决于运算放大器型号的常数。

　　因此，例如对于 LM324 a ≈ 426。滤波器Q的等效Q因子与以下表达式成比例：

　　其中b是常数（b ≈ 110）。

　　在计算中：C = C1；R = R3 + R4。因此，滤波器的“谐振”频率仅取决于元件 R = R3 + R4 和 C = C1 的标称值。比率 R2/R1 不影响“谐振”频率，而仅影响滤波器的等效品质因数的值和滤波器在“谐振”频率下的传输系数。

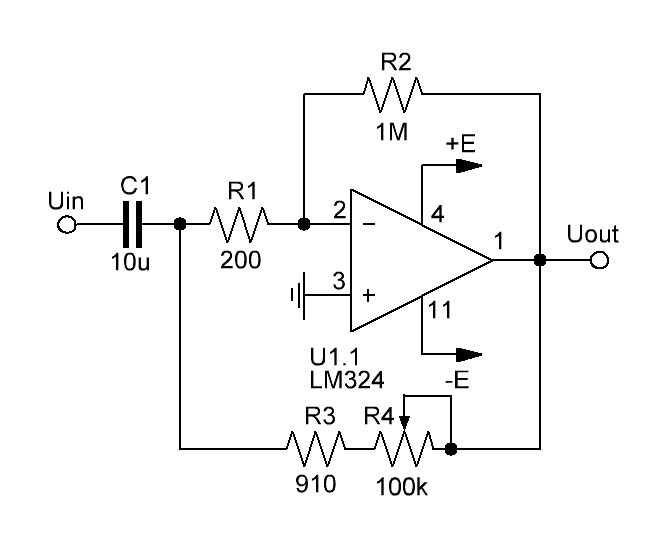
　　图 3 RC 滤波器的电气图，通过电位器 R4 调整“共振”位置。

　　RC滤波器的幅频特性如图4 所示。

　　图 4当电阻值R=R3+R4变化时，RC滤波器的幅频特性随“谐振”位置的调整而变化。
　　用电感器L1代替电容器C1，并交换频率决定元件R和L，我们得到滤波器的LR版本，如图 5所示。其幅频特性随R值的变化如图6 所示。

　　图 3 中 LR 滤波器的“谐振”频率由以下表达式确定：

　　其中f 0以 Hz 为单位，R 以 Ω 为单位，L 以 H 为单位，a为常数。比率 R2/R1 影响的参数与之前相同。

　　图 5 LR 滤波器电气图，通过电位器 R4 调整“共振”位置。

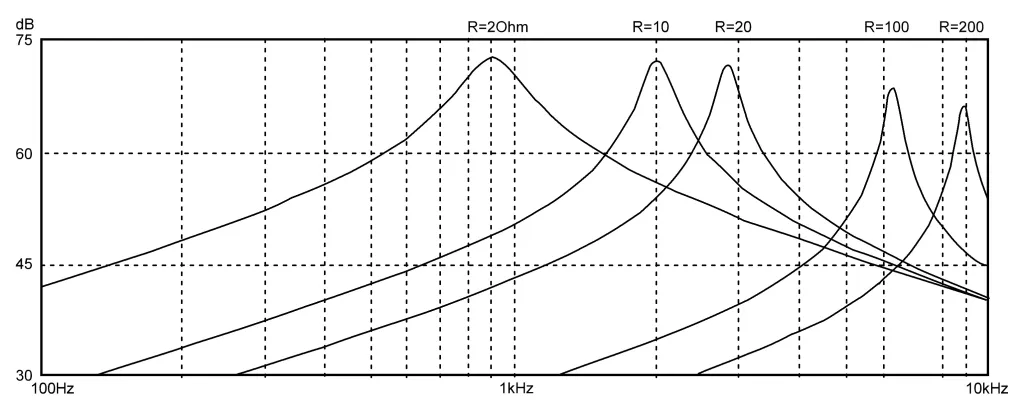
　　图6当电阻值R=R3+R4变化时，LR滤波器的幅频特性随“谐振”位置的调整而变化。