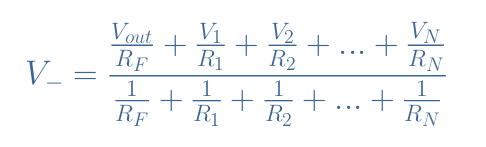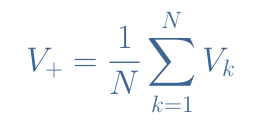在图 1中,我们看到反相求和放大器的一般电路:
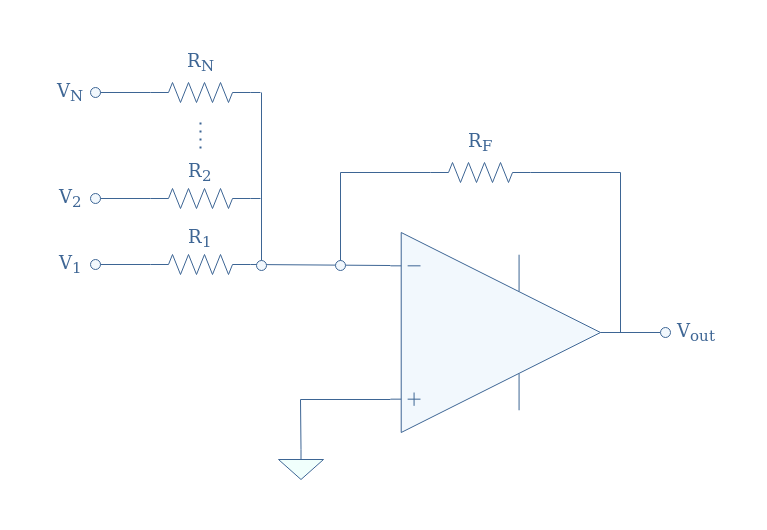
图 1:反相求和放大器电路示意图 在此配置中,N 个输入 V 1 ,V 2 ,…,V N通过不同的
电阻器 R 1 ,R 2 ,…,R N施加到
运算放大器的反相输入。输出V out通过电阻R F反馈至反相支路,同相输入端接地。我们可以将米尔曼定理应用于 V –以演示该电路的输出关系:假设理想运放 i + =i – =0,V + =V – =0,则反相求和放大器的输出关系为:
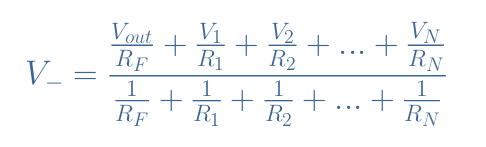
eq 1:反相求和放大器的输出公式 值得注意的是,如果我们将所有输入电阻与反馈电阻均衡,R 1 =R 2 =…=R N =R F ,我们将获得公式 1的简化版本:

eq 2:具有电阻相等条件的简化输出公式
在这种情况下,不再对总和进行加权,并且反相求和放大器将输入负相加,因为输出信号相位与输入相反。
同相求和放大器 同相求和放大器的配置与反相求和放大器类似。然而,此处的输入应用于非反相输入,而反相支路通过反馈电阻器 R F连接到运算放大器的输出,并通过电阻器 R G接地。
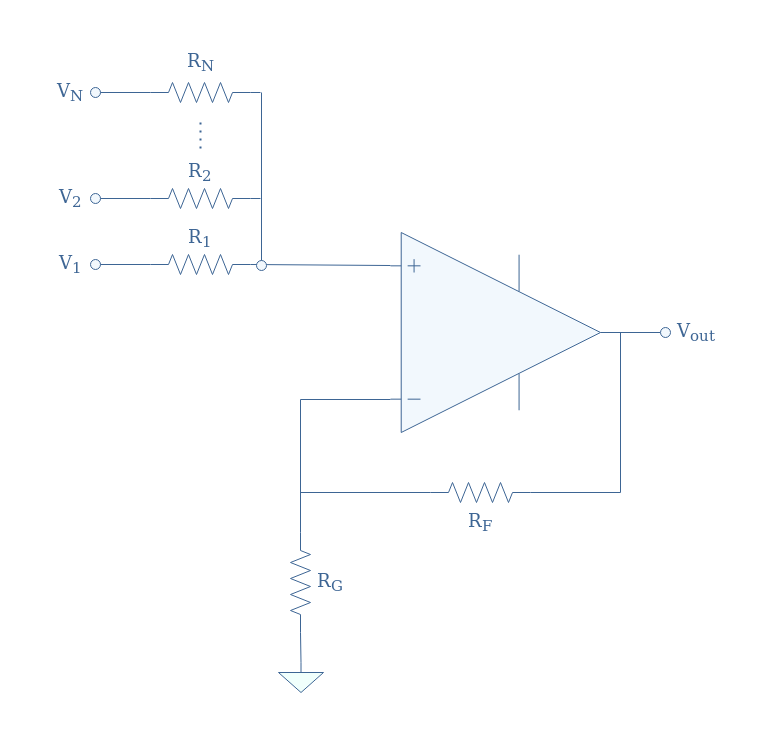
图 2:同相求和放大器电路示意图 我们可以将米尔曼定理应用于V +来演示该电路的输出关系:

由于同相配置的电压增益 V out /V in =V out /V +由1+(R F /R G )给出,因此我们可以得出结论,同相求和放大器输出的一般关系为由方程 3给出:

eq 3:同相求和放大器的输出公式 如果我们提出R=R 1 =R 2 =…=R N ,V +的表达式可以得到极大的简化,我们确实得到:
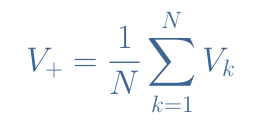
此外,我们还可以提出(1+R F /R G )=N以获得输入电压的直接和:

eq 4:具有电阻相等条件的简化输出公式
通过这两个条件,我们可以看到输出电压是输入信号的直接和,因为该和没有加权并且不存在相位差。作为本节的总结,我们可以对反相和非反相求和配置进行一些比较。反相配置的优点在于,即使在一般情况下,输出也可以简单地表示为不同电阻器和输入值的函数。在非反相配置中,输出始终与输入同相,从而省去了使用反相
缓冲器来校正信号的麻烦。此外,同相配置具有高得多的输入阻抗的特性,这有利于将所需电压从源(例如
麦克风)正确注入到运算放大器的输入端。然而,我们已经看到,只有在电路中所有电阻相等的情况下,输出电压才是简单的加权和。