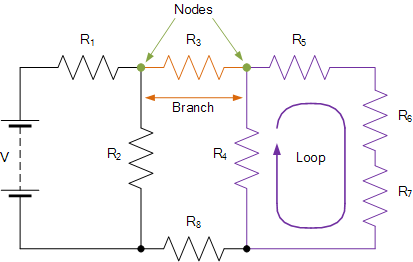
基尔霍夫电路定律

　　基尔霍夫电路定律示例 

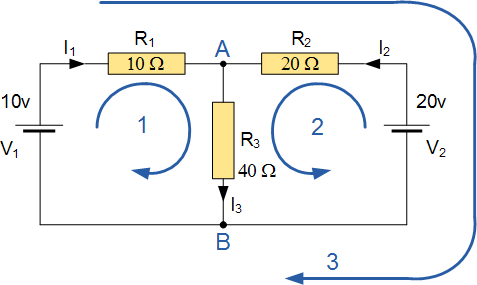
　　求40Ω电阻R 3中流动的电流
　　基尔霍夫定律示例
　　该电路有 3 个分支、2 个节点（A和B）和 2 个独立环路。
　　使用基尔霍夫电流定律KCL，方程如下：
　　在节点A  ：     I 1  + I 2  = I 3
　　在节点B  ：     I 3  = I 1  + I 2
　　使用基尔霍夫电压定律KVL，方程如下：
　　循环 1 的计算公式如下：     10 = R 1  I 1  + R 3  I 3  = 10I 1  + 40I 3
　　循环 2 的计算公式如下：     20 = R 2  I 2  + R 3  I 3  = 20I 2  + 40I 3
　　循环 3 的计算公式为：     10 – 20 = 10I 1  – 20I 2
　　由于I 3是I 1  + I 2之和，我们可以将方程重写为：
　　等式。否 1 :     10 = 10I 1  + 40(I 1  + I 2 ) = 50I 1  + 40I 2
　　等式。否 2 :     20 = 20I 2  + 40(I 1  + I 2 ) = 40I 1  + 60I 2
　　我们现在有两个“联立方程”，可以通过减法来减少I 1和I 2的值
　　将I 1替换为I 2得出的I 1值为-0.143 安培
　　将I 2替换为I 1得出I 2的值为+0.429 安培
　　如：     I 3  = I 1  + I 2
　　流过电阻器R 3的电流如下：     -0.143 + 0.429 = 0.286 安培
　　电阻器R 3两端的电压为：     0.286 x 40 = 11.44 伏
　　I 1的负号意味着初选择的电流方向是错误的，但仍然有效。事实上，20v电池正在给10v电池充电。
　　基尔霍夫电路定律的应用
　　这两条定律使得可以找到电路中的电流和电压，即该电路被称为“已分析”，使用基尔霍夫电路定律的基本程序如下：
　　1.假设所有电压和电阻均已给出（如果没有，则将其标记为V1、V2、..R1、R2等）
　　2.为每个分支或网格分配一个电流（顺时针或逆时针）
　　3.用分支电流标记每个分支。（I1、I2、I3等）
　　4.找出每个节点的基尔霍夫定律方程。
　　5.找出电路中每个独立环路的基尔霍夫第二定律方程。
　　6.根据需要使用线性联立方程求出未知电流。