在交流电路中，电感起着基础作用，这对于理解电路分析和设计至关重要。
　　电感是称为电感器的电子元件的一种特性，当电流流过电感器时就会产生电感，从而产生磁场。该磁场与电路的其他部分相互作用，导致感抗现象，这是一种对抗电流变化的形式。感抗影响电路的整体阻抗，并对信号滤波和频率响应具有重要影响。了解串联和并联配置中的电感器至关重要，因为它会影响总电感并影响电路的行为。此外，电感电路中的功率涉及电压和电流之间的相移，从而导致复杂的功率计算。
　　在电感电路中，电流的变化会产生感应电动势，根据楞次定律，感应电动势将抵抗电流的变化。在直流电路中，感应效应导致电流缓慢上升，终根据电路电阻达到大约电流的值。
　　在感应交流电路中，电流的值和方向不断变化，产生感应电动势，该感应电动势必须不断抵抗电流的变化。图 1 显示了纯电感电路的电流、感应电动势和电源电压之间的关系。
　　使用电压相量作为参考，电流相量滞后 90°，因此与电压参考成直角绘制。请记住，在电压下，电流为零但不断上升，而在零电压下，电流。
　　感抗
　　在交流电路中，电流的变化会产生与电流相反的感应电动势 (EMF)。这种电流对抗的影响称为感抗（符号 X L），以欧姆为单位测量。
　　实际上，欧姆定律规定电流等于电压除以电流的阻力。感抗是一种对电流的阻碍；也就是说，对于纯电感，I = V/ X L。
　　感抗取决于电感和电源频率，可以通过以下公式计算：
　　\[X_{L}=2\pi fL\]
　　在哪里
　　X L  = 感抗（欧姆）
　　f = 频率，单位为赫兹 (Hz)
　　L = 电感，单位为亨利 (H)
　　示例 1： 电感为 0.05 H 的线圈在频率为
　　(a) 30 赫兹和
　　(b) 60 赫兹，以及
　　\[X_{L}=2\pi fL = 2\times3.142\times30\times0.05=9.43\Omega\]
　　\[X_{L}=2\pi fL = 2\times3.142\times60\times0.05=18.85\Omega\]
　　示例 2：当施加 600 V、60 Hz 电源时，流过电感为 0.12 H 的线圈的电流值是多少？
　　\[X_{L}=2\pi fL = 2\times3.142\times30\times0.12=45.2\Omega\]
　　\[I=\frac{V}{X_{L}}=\frac{600}{45.2}=13.3A\]
　　示例 3：当施加 250 V、60 Hz 电源且通过线圈的电流为 3 A 时，扼流线圈的电感是多少？
　　\[R=\frac{V}{I}=\frac{250}{3}=83.33\Omega\]
　　\[L=\frac{X_{L}}{2\pi f}=\frac{83.33}{2\times3.142\times60}=203mH\]
　　串联电感
　　如果两个电感器串联，每个电感器都会产生一个感应电动势，并且总感应电动势将会增加。因此增加了对电流流动的阻力。通过串联放置电感器，总感抗会增加，就像串联放置电阻器会增加总电阻一样：
　　\[X_{L总}=X_{L1}+X_{L2}+X_{L3}\cdot\cdot\,\cdot+X_{Ln}\]
　　示例 4：当两个电感器（一个感抗为 10 Ω，另一个感抗为 14 Ω）串联连接到 250 V、60 Hz 电源时，
　　(a) 确定总感抗。
　　(b) 确定总电流。
　　\[X_{L总}=X_{L1}+X_{L2}+10+14=24\欧米茄\]
　　\[I=\frac{V}{X_{L}}=\frac{250}{24}=10.42A\]
　　因为感应电动势的总值增加，这意味着总电感增加。因此，以同样的方式求出总电感。
　　\[L_{总计}=L_{1}+L_{2}+L_{3}
　　\cdot\cdot\,\cdot+L_{n}\]
　　并联电感
　　如果两个纯电感器并联，则每个电感器都从电源汲取自己的电流，并且线电流是单独电流的相量和。每个电流滞后电压90°；因此，它们彼此同相并且可以算术相加。
　　因此，总感抗随着电流的增加而按比例减少，这使得我们可以使用与并联电阻器相同类型的公式。
　　\[X_{Ltotal}=\frac{1}{\frac{1}{X_{L1}}+\frac{1}{X_{L2}}+\frac{1}{X_{L3}}\cdot \cdot\cdot+\frac{1}{X_{LN}}}\]
　　在哪里
　　X Ltotal  = 总电抗
　　X L1  = 电抗 1
　　X L2  = 电抗 2
　　X L3  = 电抗 3
　　X LN  = 更多电抗
　　使用相同的方法计算并联电感器的电路的总电感
　　\[L_{总计}=\frac{1}{\frac{1}{L_{1}}+\frac{1}{L_{2}}+\frac{1}{L_{3}}\cdot \cdot\cdot+\frac{1}{L_{N}}}\]
　　在哪里
　　L总 = 总电感
　　L 1  = 电感1
　　L 2  = 电感2
　　L 3  = 电感3
　　L N  = 更多电感
　　示例 5：当两个电感器（一个感抗为 16 Ω，另一个感抗为 14 Ω）并联在 250 V、60 Hz 电源上时，
　　(a) 确定总感抗。
　　(b) 确定总电流。
　　\[X_{Ltotal}=\frac{1}{\frac{1}{X_{L1}}+\frac{1}{X_{L2}}}=\frac{1}{\frac{1}{ 16}+\frac{1}{14}}=7.468\欧米茄\]
　　\[I=\frac{V}{X_{L}}=\frac{250}{7.468}=33.48\Omega\]
　　电感电路中的功率
　　电感器将能量存储为磁场，当磁场消失时，能量返回到电路。这种情况每半个周期发生，并且由于没有电阻（理论上），因此没有损耗，并且所有能量都返回到电路。　　图 1 将施加的电压显示为红色正弦波，将反电动势显示为绿色正弦波。当电阻不存在或可忽略不计时，反电动势等于所施加的电压且极性相反，或者，正如您可能注意到的，它异相 180°。

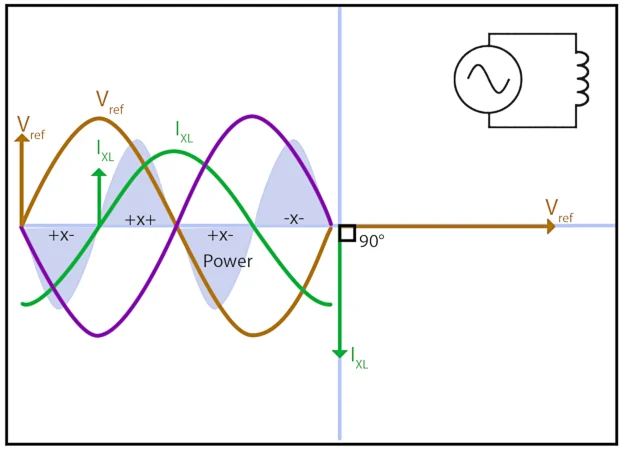
　　图 1. 感应交流电路中的功率动态。图片由 Amna Ahmad 提供
　　反电动势与电流变化成正比，因此与电流异相 90°。类似地，电流与施加的电压异相 90°，当施加的电压改变极性（即过零）时，会出现电流。
　　在图1中，功率由阴影正弦波表示，表明它的频率是电压或电流的两倍，并且有两个正功率脉冲，我们通常认为已经使用了能量。现在我们必须考虑储存在电感器中的能量。
　　然而，功率曲线的负脉冲并不意味着我们发现了负功率，而是意味着我们发现了已返回电路的能量。
　　这意味着功率波形的符号每四分之一周期反转，表明功率交替地馈入电感器和从电感器返回。
　　在电流上升期间，能量用于产生磁场，而在电流下降期间，磁场崩溃，能量恢复供电。在一个完整的周期内，功率波形的正负部分相互抵消；因此，纯电感器消耗的平均功率为零。
　　图1还表明，如果电压和电流波形是正弦波，但功率波的频率是线路频率的两倍，则功率波是正弦波。