在电感 和电阻组成的串联电路中,电流滞后电压的角度()小于 90°。图 1 显示了 RL 电路的典型电压和电流波形,以及电路中的功率波形。功率波形是通过将电压和电流的瞬时值相乘得出的。
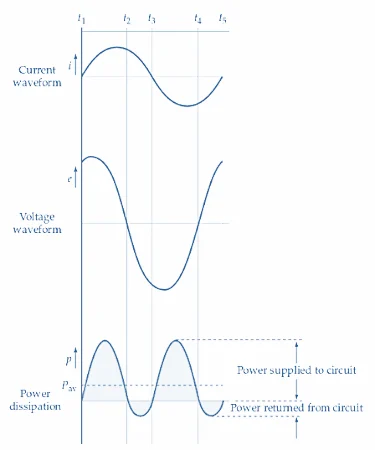
图 1. RL 电路的功率波形可以从电压和电流波形中得出。一些功率消耗在电阻中,因此功率波形的正部分和负部分不相等。图片由 Amna Ahmad 提供
在t 1 到t 2期间, i 和e 都是正值,因此幂p 在整个时间内保持正值。t 2 至t 3期间,i为正数,e为负数;因此,i和e的乘积为负,功率波形位于零线以下。t 3之后,电流和电压均为负值,直到t 4为止。因为-ei 是正数,所以从t 3 到t 4幂再次为正。
功率波形清楚地表明,向电路提供的正功率多于负功率。这是可以预料的,因为功率在电阻中消耗,但提供给电感的平均功率保持为零。提供给电路的平均功率可以用功率波形上显示的虚线表示。 现在考虑串联 RL 电路的相量图,如图 2 所示。电流 I 滞后于施加的电压 E 角度 。电阻两端的电压 (E R ) 与 I 同相,因此 E R 也滞后 E 角度 。电感两端的电压为 E L,它以 90° 的角度超前电流。E R 和E L的相量 和给出了
电源电压E,如图所示。
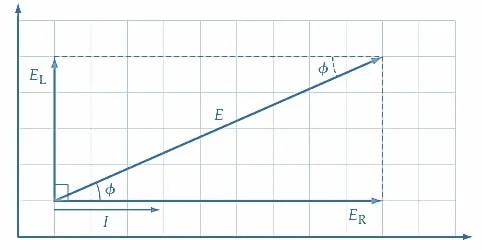
图 2. RL 串联电路的相量图。图片由 Amna Ahmad 提供
由于功率仅在电阻组件中耗散,因此电路功率为 \(P=I\times(电压\,in\,phase\,with\,I),或\,P=EI\,cos\,cos\菲\)。
当然,RL 电路中真正消耗的功率是
电阻器中消耗的功率。所以,真正的力量是
\[P=E_{R}\乘以I\]
并从图2
\[E_{R}=E\,cos\,cos\Phi\]
给予
\[P=(E\,cos\,cos\Phi)\乘以 I\]
或者说真正的力量是
\[P=EI\,cos\,cos\Phi(1)\]
无功功率是感应电压和电流 E L 和 I L的乘积。
从图2
\[E_{L}=E\,sin\,sin\Phi\]
和
\[I_{L}=I\]
所以
\[Q=EI\,sin\,sin\Phi(var)(2)\]
如果将 RL 电路中的电源电压 E 与测量到的电流 I 相乘,则乘积既不是有功功率也不是无功功率。然而,它确实给出了一个似乎是提供给电路的功率的量。术语视在功率 (S) 应用于该量,视在功率的单位为伏安 (VA):
视在功率
\[S=EI(3)\]
其中 S 是视在功率,E 和 I 是电源电压和电流的有效值。
实施例1
在提供 50 V 电压的串联 RL 电路中,测得的电流为 100 mA,相位角为 25°(图 3)。计算提供给电路的视在功率、无功功率和真实功率。
解决方案
公式3
\[S=EI\,伏安=50V\times100mA=5VA\]
等式2
\[Q=EI\,sin\,sin\Phi\,var=50V\times100mA\times{\Big(}sin\,sin\,25\ Degree{\Big)}\approx2.1var\]
公式1 \[P=EI\,cos\,cos\Phi 瓦=50V\times100mA\times{\Big(}cos\,cos\,25\度{\Big)}\约4.5W\]
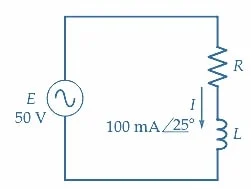
图 3. 示例 1 的电路。所用图像由 Amna Ahmad 提供



