了解输入端寄生电容的影响以及如何在模拟电路设计中对其进行补偿。
大多数内部补偿
运算放大器旨在在任何与频率无关的闭环增益(包括单位增益)下稳定运行。
实际上,电容的存在,无论是有意的还是寄生的,都会使电路不稳定,并且可能需要用户采取额外的补偿措施来恢复可接受的相位裕度。
在采样保持电路、峰值检测器和具有输出电容旁路的电压参考升压器中可以找到有意输出电容的示例。(关于容性负载补偿,请参阅我关于如何使用运算
放大器电路驱动大容性负载的文章。)
本文将讨论输入端(尤其是反相输入端)寄生(或杂散)电容的影响。
输入电容的类型
所有运算放大器均具有差模输入电容C dm和共模(输入连接在一起)输入电容C cm。这些是输入级
晶体管以及输入保护
二极管(如果存在)所表现出的电容。(尽管C dm和C cm位于运算放大器内部,但我们将它们显示在外部以获得更好的可视化效果。)
在物理电路中,额外的电容在外部发挥作用,例如
电阻器、其引线以及印刷电路走线的杂散电容。 在图1b的放大器示例中 ,与反相输入相关的所有寄生效应都已集中到单个等效电容C n中。
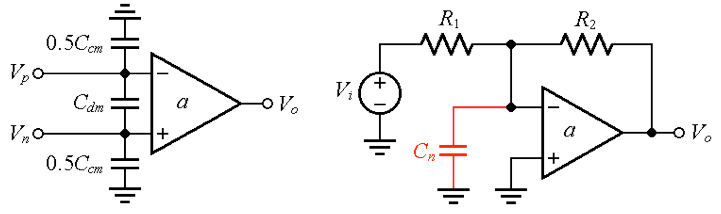
(一) (二)
图 1. (a) 运算放大器的杂散输入电容。(b) 将与反相输入相关的所有寄生参数集中在一起作为单个电容 C n。
让我们通过闭合率 (ROC)研究C n对电路稳定性的影响。为此,我们将输入源设置为零,如图 2a(如下)所示断开环路,施加测试电压V t,并计算反馈因子 ( jf ) 为

公式1
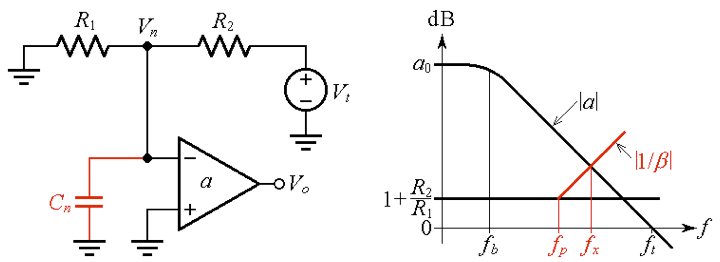
(一) (二)
图2 . (a) 求反馈因子 ?(jf)。(b) 接近率 (ROC) 接近 40 dB/dec。
在哪里
公式2

代入方程(1),经过一些代数运算后,我们得到:

公式3
在哪里
公式4

如果我们关注方程(4)的物理意义,我们会看到C n和电阻R 1 || 由周围电路提供给它的R 2在反馈环路内建立极点频率。因此,围绕环路传播的信号将不得不与两个极点竞争,一个由运算放大器引起,另一个由C n引起,相移有接近 180° 的风险,从而危及电路稳定性。
我们可以在图 2b中更好地形象化这一点,它显示了开环增益 |a| 的图。以及反馈因子 |1/ ? ( jf )|的倒数,其中
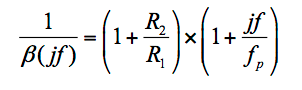
公式5
( jf )的极点频率 f p是 1/ ? ( jf )的零频率,表明 |1/ ? ( jf )| 曲线在f p处开始上升。如果f p与交叉频率f x相比足够低,则闭合率将接近 40 dB/dec,表明相位裕度接近于零。
如何减轻单个等效电容造成的相位滞后
解决C n造成的相位滞后的常见方法是通过R 2上的反馈电容C f引入相位超前,如图 3 所示。

图3 . 利用 C f引入的相位超前来对抗 C n引起的相位滞后。
如果我们将R 2替换为Z 2 ( jf ) = R 2 ||( 1/j2πificC f ) ,方程 (1) 仍然成立。经过一些代数运算后,这给出了
公式6

公式 7
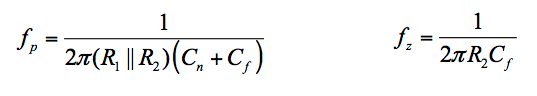
这里需要注意的是,反馈电容的存在为? ( jf ) 创建了零频率 f z,同时也稍微降低了现有的极点频率f p(回想一下 的极点/零变为?的零/极点) 1/ β)。
如何选择反馈电容
选择C f 有两种常见方法:
f z = f p
f z = f x
f z = f p
施加f z = f p ,以便零抵消方程 (6) 中的极点,从而始终给出 1/ ? = 1 + R 2 / R 1,如图 4a所示。

(一) (二)
图 4.对于相位裕度 ? m ≈ 90°,施加 (a) f z = f p ,或对于 ? m ≈ 45° 施加 (b) f z = f x。
等式(7)中的f z和f p等式化简后可得出:
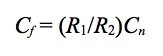
公式8
C f的选择导致相位裕度约为 90°。为了找到交叉频率f x,我们利用 | 上增益带宽积的恒定性。一个| 曲线写成 (1 + R 2 / R 1 ) × f x = f t,所以
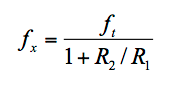
公式 9
请注意,闭环增益有两个极点频率f z和f x,其 –3dB 频率接近f z。
f z = f x
如图 4b所示,施加f z = f x ,相位裕度约为 45°。闭环增益现在将具有更高的–3dB 频率,但代价是出现一些峰值和振铃。
要找到所需的C f,我们必须首先找到f x。考虑到 1/ ?的高频渐近线为 1 + C n / C f,我们再次利用 | 上增益带宽积的恒定性。一个| 曲线写为 (1 + C n / C f ) × f x = ft,因此f x = f t /(1 + C n / C f )。
施加f z = f x意味着施加 1/( 2πR 2 C f ) = f t /(1 + C n / C f )。预期C n / C f >> 1,我们近似 1/( 2πR 2 C f ) ≈ f t /( C n / C f ) = f t C f / C n,我们求解C f得到
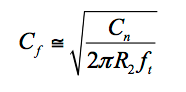
公式10
请注意,闭环增益现在在f x处具有两个重合的极点频率。
通过 PSpice 验证
我们希望通过图 5 的电路来验证上述考虑因素,该电路使用f t = 10 MHz的恒定增益带宽运算放大器。
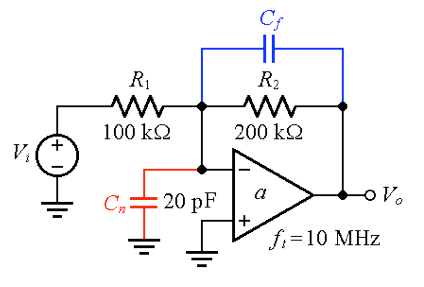
图5 . 增益为 –2V/V 的反相放大器示例。
现在我们看一下图6:

图 6.用于绘制 |a| 的 PSpice 电路 和|1/?|。(b)|1/?| 不同 C f值的曲线。
参考图6,我们进行以下考虑:
在没有补偿的情况下 ( C f = 0),交越频率测量为f x ≈ 625 kHz,相位角测量为 ph[ a ( jf x )] ≈ –90° 和 ph[1/ ( jf x ) ] ≈ 79.2°,所以
m = 180° + ph[ a ( jf x )] – ph[1/ ? ( jf x )] ≈ 180 – 90 –79.2 = 10.8°
公式 11
表明电路处于振荡边缘。
对于? m ≈ 90°的相位裕度,我们使用公式 (8) 得到C f = 10 pF。根据方程 (9),我们得到f x ≈ 3.33 MHz。如图 6b所示,我们现在有
m ≈ 90°。
对于 m ≈ 45°,我们使用方程 (10) 得到C f = 1.262 pF。使用 PSpice 的光标,我们现在测量f x = 762.1 kHz 和 m = 58.8°。这比预期的 45° 更好。要了解原因,请使用公式(7)计算f p = 112.28 kHz 和f z = 630.57 kHz,然后使用公式(6)计算
然后,按式(11)求出 m = 180°– 90 –31.2 = 58.8°。
闭环交流响应
图 7 所示为所考虑的三种情况的闭环交流响应。

图 7.使用 PSpice 绘制不同 C f值的闭环交流响应。
正如预期的那样,未补偿的响应表现出相当大的峰值。当C f = 1.262 pF 时,峰值几乎无法察觉,在这种情况下,响应在约 762 kHz 处表现出一对重合的极点频率。C f = 10 pF的响应迟缓,这是我们为大相位裕度付出的代价。
如前所述,该响应包含两个极点频率,即f z和f x。 图 8 所示的是阶跃响应,在讨论了交流响应之后,应该是不言自明的。

图 8.使用 PSpice 绘制不同 Cf 值的闭环阶跃响应。






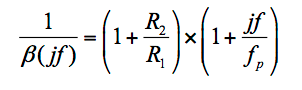


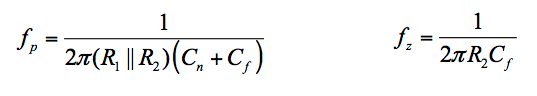

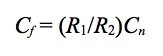
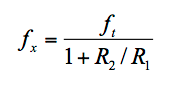
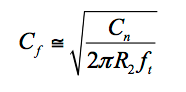

 图 6.用于绘制 |a| 的 PSpice 电路 和|1/?|。(b)|1/?| 不同 C f值的曲线。
图 6.用于绘制 |a| 的 PSpice 电路 和|1/?|。(b)|1/?| 不同 C f值的曲线。
