压控滤波器（VCF）是模拟合成器的支柱。但有一个过滤器比其他过滤器高出一筹，因为它富有创意、有效，而且（我有充分的权威）听起来“才华横溢”： 穆格梯形过滤器。
　　在本系列中，我们将从小信号开环分析开始分析穆格梯形滤波器的行为。
　　在上一篇文章中，我们回顾了过滤器的主要元素并分析了驱动程序部分。现在，我们将分析拓扑的（滤波器部分）并表达整个滤波器的小信号开环传递函数。
　　在第 1 部分中，我们看到了 Moog 梯形滤波器的完整原理图，并将其简化为图 1 所示的形式。 　　
　　图 1. Moog 滤波器
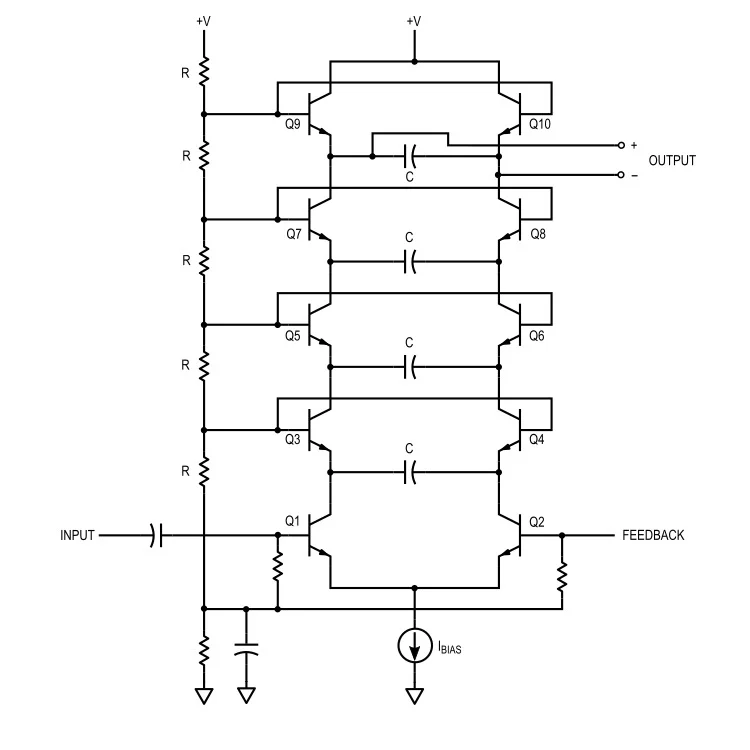
　　　　我们将拓扑分为三个元素：
　　驾驶台
　　中间过滤级
　　输出滤波器级
　　这三个阶段如图 2 所示。
　　　　图 2. 梯形滤波器拓扑的三个要素。(a) 驱动差分对。(b) 中阶梯低通滤波器部分。(c) 顶部的输出滤波器部分。　
　　同样在第 1 部分中，我们得出了驱动级中电压和电流之间的关系，如上面的图 2(a) 所示。现在，我们将分析图 2(b) 和 2(c) 中所示的滤波器级。
　　穆格滤波器的各个滤波器
　　滤波器部分彼此相似，只是一个滤波器部分驱动梯子中的另，而另一个则连接到电源。两者的工作机制相同，因此我们仅分析图 3 所示的机制。
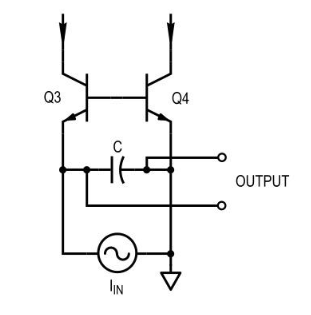
　　　　图 3.  Moog 滤波器中的一个滤波器部分，具有差分驱动电流。　　
　　对于小信号分析，我们可以进行以下简化，如图4、5、6和7所示。
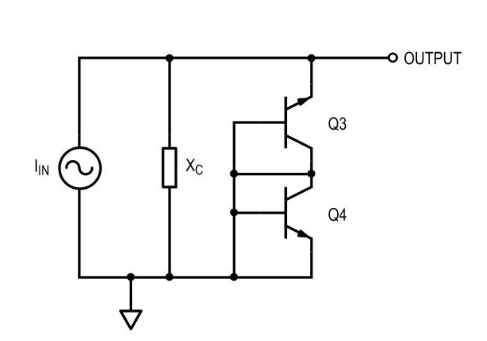
　　　　图 4. 利用基极保持恒定电位并将电容器作为电抗的事实。
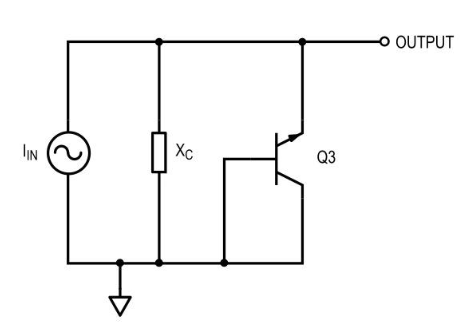
　　　　图 5. 拆下短路的晶体管。　　
　　图 6. 晶体管 Q3 以二极管配置连接，因此我们可以用二极管示意性地替换它。
　　

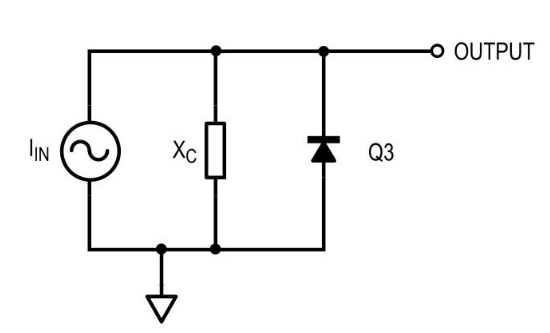
　乍一看，图 7 中的电路可能不像滤波器。 　

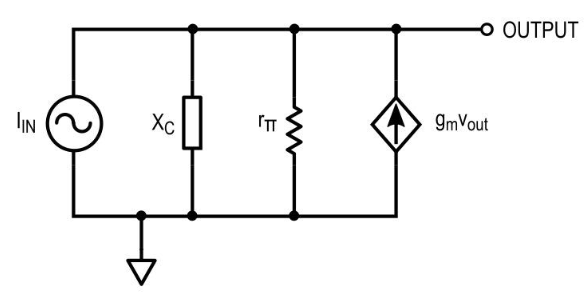
　　图 7. 二极管/晶体管终被替换为混合 pi 模型。
　　
　　这是公平的——这样的电流驱动 RC 电路并不常见。但是，注意到两个并联组件充当分流器而不是分压器，它就开始有意义了。
　　随着容抗 X c减小（随着频率增加），电容器两端的电压减小。
　　该电路的输出电压是电容器两端的电压，并将传递函数描述为跨阻 r tr，我们发现：　　
　　$$ r_{tr} = \frac{v_{out}}{i_{in}} = \frac{-1}{2j \omega C + g_m} $$　　
　　在哪里　　
　　$$g_m = \frac{I_C}{V_T}$$　　
　　对于晶体管偏置（驱动）电流 I C，我们假设高贝塔值。
　　对于中间滤波器级，输出电流 g m v out成为下一部分的输入电流。该电流为：　　
　　$$ i_{输出} = i_{输入} \frac{-g_m}{2j\omega C + g_m} $$　　
　　这是我们计算开环增益所需的其他结果。
　　总结这个滤波器部分：我们已经证明，输入电流会导致电容器两端产生电压降，该电压降与容抗成正比。随着频率的增加，电压降低，从而产生低通作用。它就像电容器和晶体管等效基极阻抗（跨导）之间的电流驱动 RC 滤波器。对于中间级，晶体管电流用作下的输入电流，而电容器电压本身作为顶层的输出。
　　综合起来：计算开环增益
　　我们已经描述了驱动器和滤波器部分的传递函数。现在我们准备计算开环增益。对于n 个滤波器级，我们可以结合之前的结果（一个驱动器、n-1 个中梯滤波器部分和一个输出滤波器部分），并以输出电容器的左侧为正来查找：　
　　$$ v_{out} = \left ({g_m v_{in}}\right ) \left ( \frac{-g_m}{2j\omega C + g_m} \right )^{n-1} \left ( \ frac{-1}{2j\omega C + g_m} \right ) $$　
　　这简化为：　
　　$$ v_{out} = \pm v_{in} \left ( \frac{g_m}{2j\omega C + g_m} \right )^{n} $$　
　　其中 $$v_{out}$$ 对于n偶数为正，对于n奇数为负。开环电压增益为：　
　　$$ A = \pm \left ( \frac{g_m}{2j\omega C + g_m} \right )^{n} $$　
　　利用 $$g_{m}$$ 约等于 $$\frac{1}{{r_e} '}$$ 的事实，我们可以将其重写为更熟悉的形式，　
　　$$ A = \pm \left ( \frac{1}{j\omega r_e'C + 1}\right )^n $$　
　　您可能会注意到，它与 RC 低通滤波器的传递函数非常相似，　　
　　$$ A = \frac{1}{j\omega RC - 1} $$　　
　　我们将在下一篇文章中详细讨论这一点。
　　
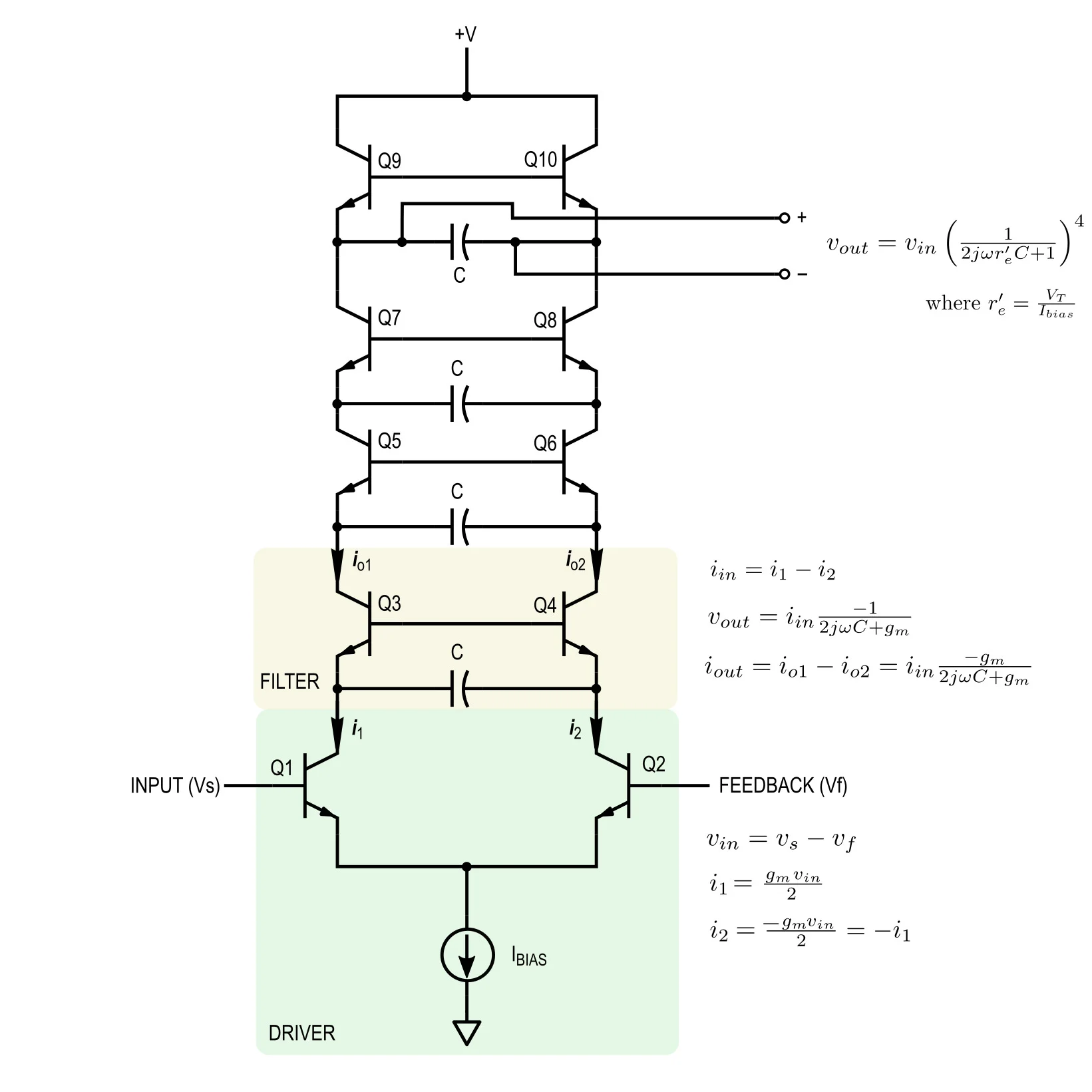
　　图 8. Moog 梯形滤波器行为总结。点击放大。
　　
　　我们可以将 Moog 滤波器的行为总结如下（参见图 8）：偏置电流设置晶体管的静态点，并且该电流在阶梯的两侧共享。
　　忽略反馈，左侧的输入电压驱动小信号电流通过支路。分支之间的差分信号在电容器上产生电势差，从而允许发生“滤波”。看待这个问题的一种方法是，晶体管的跨阻抗与电容器一起创建一个 RC 滤波器。
　　输出（作为顶部电容器的电位）取决于流过该电容器的小信号电流。
　　到目前为止，我们假设了一些重要的事情：
　　所有晶体管共享相同的贝塔值（即它们全部匹配）。
　　通过每个晶体管基极的电流可以忽略不计。
　　晶体管充当理想的相关电流源（无早期效应）。
　　所有晶体管都在有源区偏置。
　　驱动级共模电压可以忽略不计。
　　偏置电流源是理想的。
　　即使有了这些理想化，电路仍会受到温度依赖性的影响（隐藏在 g m项和晶体管 beta 中）。然而，请记住，该电路用于模拟合成器，这些缺陷被认为赋予了滤波器“特性”。