布尔代数运算可以与电子电路相关，其中输入和输出对应于布尔代数的语句。尽管这些电路可能很复杂，但它们都是由三个基本器件构成的。它们是“与”门、“或”门和“非”门。简化和组合逻辑门的基本规则被称为布尔代数，以纪念乔治·布尔（George Boole，1815 – 1864 年），他是一位自学成才的英国数学家，发展了许多基本思想。
　　逻辑门是计算机的基本构建模块。根据所使用的应用，它们由一到六个或更多晶体管物理投入运行。门至少有一个输入，只有一个输出。输入和输出值是逻辑值 true 和 false 或 1 和 0。　　　

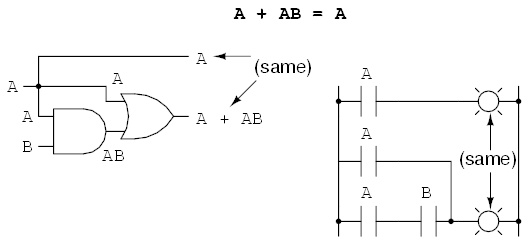
布尔代数定律

　　布尔代数的基本定律涉及允许改变加法和乘法位置的交换律、允许消除加法和乘法括号的结合律、允许对表达式进行因式分解的分配律。
　　1. 交换律 – 在该定律中，反转变量相加或相乘的顺序，而不改变表达式的真实性。
　　(a) A + B = B + A
　　(b) AB = BA
　　2. 结合法 – 该法允许删除表达式中的括号并对表达式进行重新组合。
　　(a) (A + B) + C = A + (B + C)
　　(b) (AB) C = A (BC)
　　3. 分配律——该法则允许对表达式进行乘法或因式分解。
　　(a) A (B + C) = AB + AC
　　(b) A + (BC) = (A + B) (A + C)
　　4. 身份法 – 在本法中，术语 OR 与 0 或 AND 与 1 在该术语中始终相等
　　(a) A + A = A
　　(b) AA = A
　　5. 幂等定律——在此定律中，输入与自身的 AND 或与自身的 OR 等于该输入。
　　（A）。A + A = A
　　(b) A 。一个=一个
　　6. 德摩根定律 – 该定律用于简化布尔方程，以建立仅涉及一种门的方程，通常仅使用 NAND 或 NOR 门。它还以相反的形式说明了相同的等价性，即反转任何门的输出都会给出与具有反转输入的相反类型的 AND 或 OR 门相同的功能。　　　

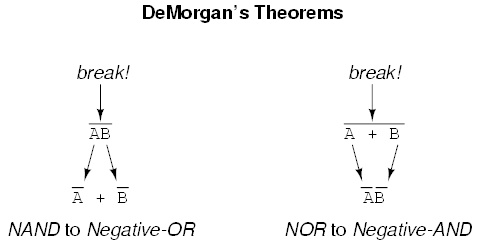
当表达式中存在多个级别的表达式时，只能打断一个条，通常先打断上面的条来开始简化会更容易。为了演示表达式 (A + (BC)')' 并使用德摩根定理求解它。

　　　

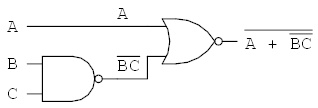
　德摩根定律示例：

　　(A (非 B)) + ((非 A) B) = 非 (((非 A) + B) (A + (非 B)))