当您查看此图时，请尝试花一点时间欣赏负面反馈的优雅。

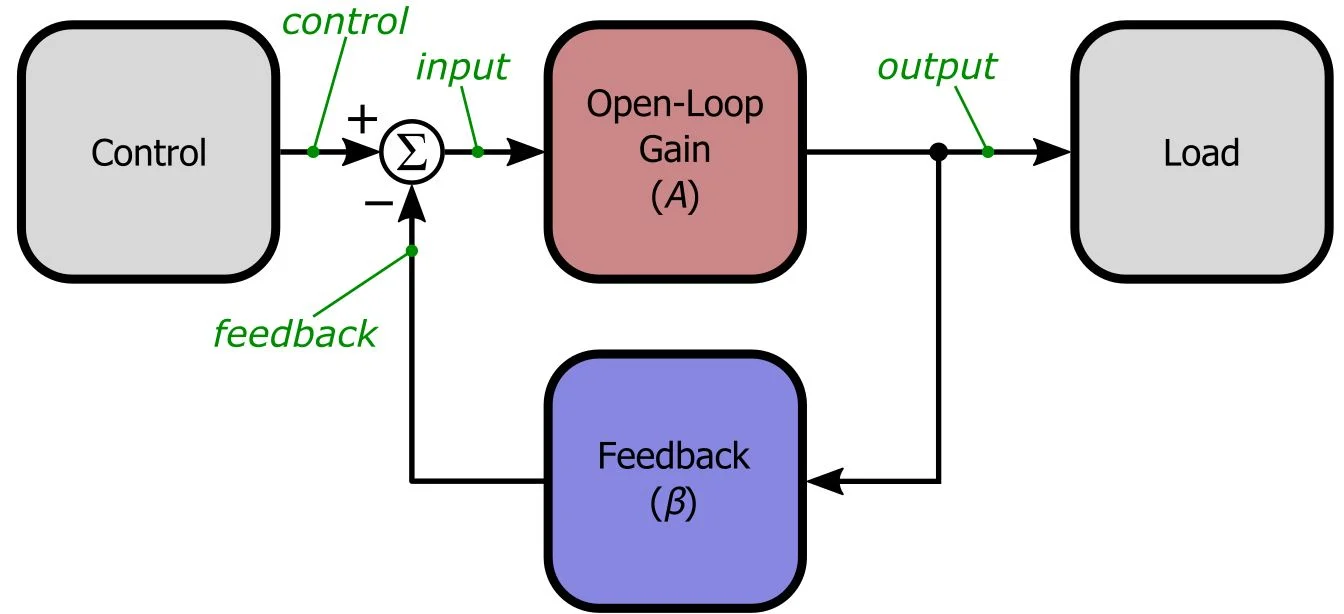
    通过简单地从参考信号中减去实际输出值（乘以 β ）并将结果用作开环放大器的输入，即使在输入输出关系不一致或复杂的情况下，我们也可以控制负载。
    这里的关键参数是A和β。绿色斜体标签代表流经系统的信号的变量名称；我们使用单词（在本文中也是斜体）而不是下标变量，希望即将进行的分析不会显得比实际情况更直观。（不过，我们保留A和β ，因为没有A和β的反馈放大器就不是反馈放大器。）    那么A和β到底是什么？关于A没有太多可说的：它是整个系统在没有反馈的情况下应用的放大。在运算放大器电路的背景下——这种比较特别合适，因为运算放大器是理论反馈放大器的直接表现——A对应于运算放大器的开环增益。β并不是那么简单：反馈因子β决定了有多少输出信号被反馈到减法节点。您可以将β视为从控制中减去的输出百分比（以小数表示）。当您考虑基本的同相运算放大器电路时，这一点应该会变得更加清楚：

    我们用来设置增益的两个电阻只不过是一个分压器网络，它将一定百分比的输出施加到运算放大器的反相端子。输出电阻器两端的电压由比率 R 1 /(R 1 + R 2 ) 乘以电阻器对两端的电压表示。因此，反馈并从控制中减去的输出的百分比（以小数表示）——即反馈因子β——为R 1 /(R 1 + R 2 )。培养对这个概念的直观理解是值得的，因为β当我们讨论稳定性时，将在以后的文章中突出显示。
    关于A和β 的另一点注意事项：它们不必只是常数，如A = 10 6和β = 0.1。它们也可以表示为频率的函数，这意味着A或β的值根据通过放大器系统的信号频率而变化。这与A尤其相关——内部补偿运算放大器的开环增益在低至 0.1 Hz 的频率下开始滚降！