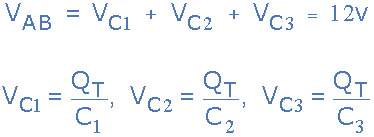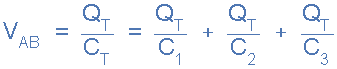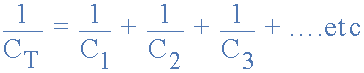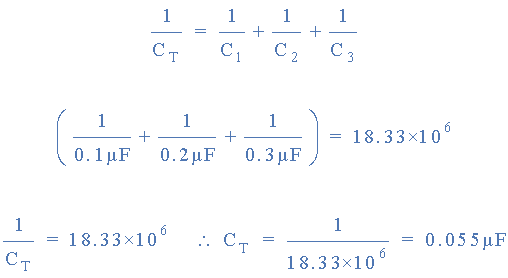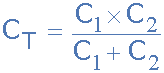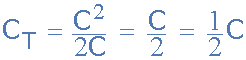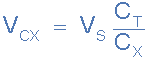
在前面的并联电路中,我们看到电路的总电容C T等于所有单个电容器加在一起的总和。然而,在串联电路中,总电容或等效电容C T的计算方式不同。
在电容器右侧板上方的串联电路中,C 1连接到第二电容器C 2 的左侧板,第二电容器C 2的右侧板连接到第三电容器C 3的左侧板。那么这种串联意味着在直流连接的电路中,电容器C 2与电路有效隔离。
其结果是有效极板面积已减小至串联链中连接的个体电容。因此,每个电容器两端的电压降将根据各个电容的值而不同。 然后将基尔霍夫电压定律 ( KVL ) 应用到上述电路中,我们得到:
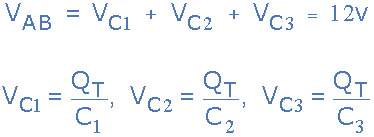
通过串联电容器的电流 由于Q = C*V并重新排列V = Q/C,因此将Q/C替换为上述 KVL 方程中的每个电容器电压V C将得出:
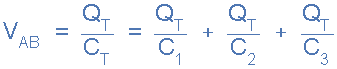
电路电流 每一项除以Q得出
串联电容器方程
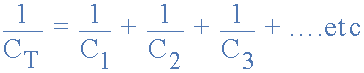
电容器串联方程
将串联电容器相加时,各个电容器的倒数 ( 1/C ) 全部相加(就像并联电阻一样),而不是电容本身。那么串联电容器的总值等于各个电容的倒数之和的倒数。
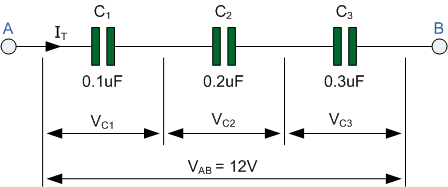
教程示例 No1 采用上述示例中的三个电容器值,我们可以计算出三个串联电容器的总等效电容C T为:
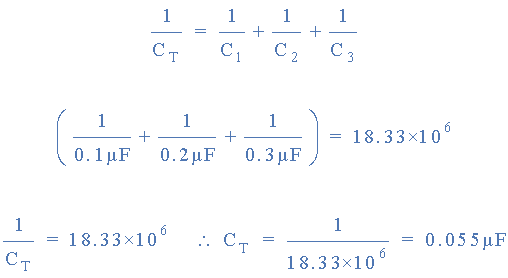
总串联电容
关于以串联配置连接在一起的电容器,需要记住的重要一点。 任意数量串联在一起的电容器的总电路电容 ( C T ) 将始终小于串联串中
小电容器的值。在上面的示例中,总电容 C T 计算为 0.055μF,但串联链中电容器的值仅为0.1μF。 这种倒数计算方法可用于计算单个串联网络中连接在一起的任意数量的单个电容器。然而,如果只有两个串联电容器,则可以使用更简单、更快速的公式。给出如下:
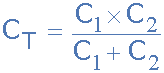
串联总电容 如果两个串联电容相等且阻值相同,即:C 1 = C 2,我们可以将上式进一步简化如下,求出串联组合的总电容。
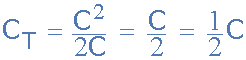
等值电容器
那么我们可以看到,当且仅当两个串联的电容器相同且相等时,总电容C T将恰好等于电容值的二分之一,即:C/2。
对于串联电阻,串联电路上所有压降的总和将等于施加的电压V S(基尔霍夫电压定律),对于串联电容器也是如此。
对于串联电容器,电容器的容抗由于
电源频率而充当阻抗。该容抗在每个电容器上产生压降,因此串联的电容器充当容性
分压器网络。 结果是,应用于
电阻器的分压器公式也可用于查找串联的两个电容器的单独电压。然后:
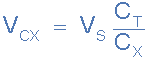
串联电容器两端的电压
其中:C X是相关电容器的电容,V S是串联链上的电源电压,V CX是目标电容器上的压降。