在 L 亨利的纯感性（即无限电容，C = ∞ 和零电阻，R = 0）电路中，电压和电流波形不是同相的。每当将变化的电压施加到纯电感线圈时，线圈就会由于其自感而产生“反”电动势。这种自感会阻碍并限制线圈中流动的电流的任何变化。

该反电动势的影响是，电流不能立即通过线圈与施加的电压同相增加，导致电流波形在电压波形之后的某个时间达到其峰值或值。结果是，在纯电感电路中，电流总是“滞后”(ELI) 于电压 90 o (π/2)，如图所示。

纯电感电路

上面的波形向我们展示了纯电感线圈上的瞬时电压和瞬时电流作为时间的函数。电流 I max出现在电压（峰值）值之后的四分之一周期 (90 ° ) 处。这里显示的电流在电压周期开始时具有负值，并在电压波形在 90 °处达到值时通过零增加到其正值。

因此，由于电压和电流波形不再一起上升和下降，而是在线圈中引入 90 o (π/2)的相移，因此电压和电流波形彼此“异相”。另一种是电压超前电流 90 o。由于电压波形和电流波形之间的相位差为 90 °，因此相位角 cos 90 °  = 0。

因此，纯电感器存储的电功率 Q L由下式给出：

纯电感器的实际功率

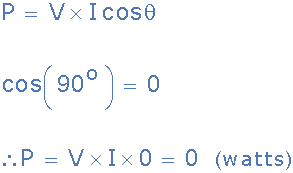
显然，纯电感器不会消耗或耗散任何实际功率，但由于我们同时具有电压和电流，因此在表达式中使用 cos(θ)：对于纯电感器，P = V*I*cos(θ)不再有效。在这种情况下，电流和电压的乘积是虚功率，通常称为“无功功率”，( Q )以无功伏安(VAr)、无功千伏安(KVAr)等为单位测量。

无功伏安 (VAr) 不应与用于有功功率的瓦特 (W) 混淆。VAr 表示彼此相差90 °的伏特和安培的乘积。为了从数学上确定无功平均功率，使用正弦函数。那么电感器中的平均无功功率的方程变为：

纯电感器中的无功功率

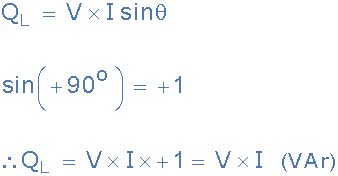
与有功功率 (P) 一样，无功功率 (Q) 也取决于电压和电流，还取决于它们之间的相位角。因此，它是所施加的电压和电流分量的乘积，电流分量与电压呈 90 °异相，如图所示。

纯电感器的交流波形

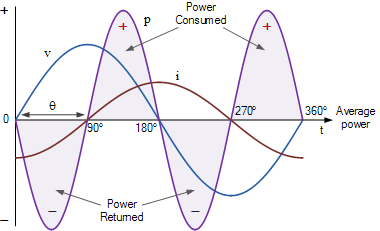
在 0 °和 90 °之间的电压波形的正半部分中，电感电流为负，而电源电压为正。因此，伏特和安培的乘积给出负功率，即负乘以正等于负。在 90 °和 180 °之间，电流和电压波形均为正值，从而产生正功率。该正功率表明线圈正在消耗来自电源的电能。

在180 °和270 °之间的电压波形的负半部分，有负电压和正电流，表示负功率。该负功率表明线圈正在将存储的电能返回到电源。在 270 °和 360 °之间，电感电流和电源电压均为负值，从而产生一段正功率。

然后，在电压波形的一个完整周期内，我们有两个相同的正负功率脉冲，其平均值为零，因此没有用完实际功率，因为功率交替流向和流出电源。这意味着纯电感器在一个完整周期内消耗的总功率为零，因此电感器无功功率不执行任何实际工作。