在这两篇文章的第二篇文章中，我使用LTspice 来评估不完美的电阻器匹配对电路误差的影响，其中误差计算为模拟负载电流与应用笔记中给出的公式预测的负载电流之间的差异。

IOUT=VIN(R4R2)R1

    不完全匹配是通过使用 LTspice 的蒙特卡罗函数在指定容差范围内改变 R3 和 R5 的值来模拟的。输出电流的大小与 R1、R2 和 R4 的值成正比，这三个电阻保持在其标称值。
    在本文中，我们将对现实生活与理论性能进行更全面的模拟。所有电阻器都有 0.1% 的容差，我们还将考虑工作温度的变化。这里的目标是实际了解在现实生活条件下我们可以期望从该电路获得多少精度。
    在特定温度下进行模拟
    LTspice 中包含的一些运算放大器组件会随温度变化而变化，而有些则不会。如果有一种方便的方法来确定哪些是哪些，我一直找不到，所以我只是使用猜测和检查的方法。
    我们在之前的仿真中使用的 LT1001A 不属于温度依赖型类别。在测试了其他一些不符合要求的运算放大器后，我发现 AD8606 是一款用于低压应用的精密运算放大器，其宏模型中的某处具有温度依赖性。
    我们可以通过“temp”指令将温度合并到 LTspice 的电路计算中。例如，“.temp -40 125”将在 –40°C 下执行模拟，在 +125°C 下执行另一个模拟。
    以下电路表明运算放大器在不同温度下是否会产生不同的结果。

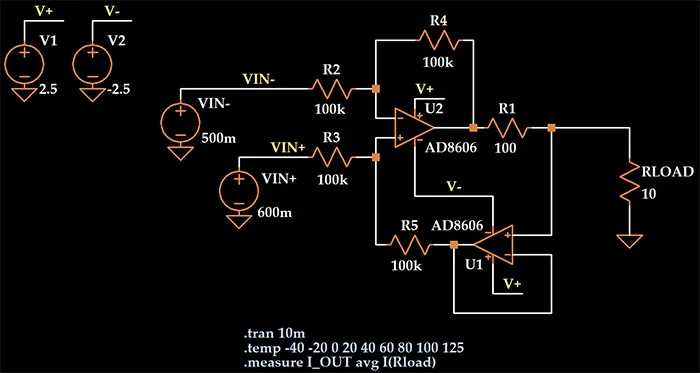
    预期输出电流为 (0.6 V – 0.5 V)/(100 Ω) = 1 mA。以下是在“temp”指令中指定的温度下获得的模拟输出电流值：

    温度变化的蒙特卡洛模拟
    当我们将蒙特卡罗函数（LTspice 中的“mc”）应用于电阻值并使用“.step param run ...”指令时，仿真将包含多个独立运行，并且对于每次运行，mc函数将从指定公差确定的范围内选择一个新值。
    我们假设预期应用需要在整个汽车温度范围（–40°C 至 +125°C）内发挥功能。这也恰好是 AD8606 的工作温度范围。如果我们添加一个“temp”指令，运行次数将乘以列表中的温度数。
    在该范围内包含大量温度会导致仿真时间过长，并且很难想象有必要这样做的场景。运算放大器不会因工作温度的适度升高或降低而表现出严重的性能波动。
    事实上，前面的图表明温度的影响是单调的并且非常微妙。因此，我认为我们可以通过选择覆盖整个范围的几个温度来充分考虑温度影响。
    这是我用于电阻容差加温度模拟的原理图：

    这是 900 次运行（每个温度 100 次运行）的模拟负载电流图。

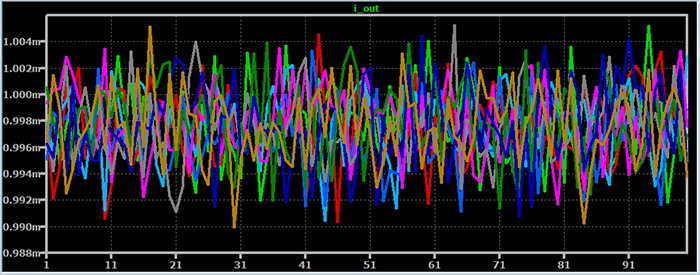
    性能统计
    我的下一步是将结果导出为文本文件，然后将文本文件导入 Excel 以进行进一步分析。为此，右键单击绘图并选择文件 -> 将数据导出为文本。这是我将文本文件导入 Excel 后数据的样子：

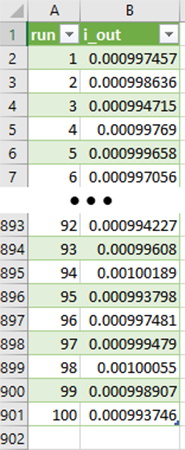
    现在我可以轻松计算出我感兴趣的任何统计数据。平均值为 0.9977 mA，因此运算放大器中的某些非理想情况会产生一个小偏移（0.0023 mA，或预期输出电流的 0.23%）。标准偏差为 2.86 A，值和值分别为 1.0053 mA 和 0.9899 mA。
    我发现和结果非常令人印象深刻：即使所有电阻器都具有 0.1% 的容差并且温度在很宽的区间内变化，我可以预期负载电流在正方向上与所需电流的偏差不会超过约 5 ?A和 10 ?A 在负方向。