电感线圈和螺线管不是纯电感设备，而是由连接在一起的电感和电阻组成的基本 LR 串联电路。
    在本节关于电感器的个教程中，我们简要地查看了电感器的时间常数，指出流经电感器的电流不会瞬时变化，但会以恒定速率增加，该速率由内部的自感应反电动势决定感应线圈。
    换句话说，电路中的电感器会阻止电流 (i) 通过它。虽然这是完全正确的，但我们在教程中假设它是一个理想电感器，其线圈绕组没有电阻或电容。
    然而，在现实世界中，“ALL”线圈无论是扼流圈、螺线管、继电器还是任何缠绕元件，无论多么小，总是会有一定的电阻。这是因为用于制造它的实际线圈匝数使用具有电阻值的铜线。
    然后出于现实世界的目的，我们可以将我们的简单线圈视为与“电阻” R串联的“电感” L。换句话说，形成一个LR 串联电路。
    LR串联电路基本上由电感 L 与电阻 R 串联的电感器组成。电阻“R”是构成电感器线圈的线匝或环路的直流电阻值。考虑下面的 LR 串联电路。

    LR系列电路

    lr串联电路

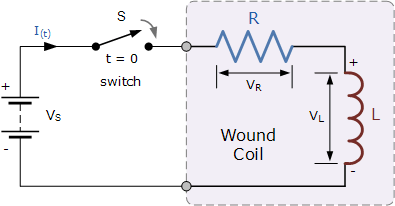
    上述LR 串联电路跨接在恒压源、（电池）和开关之间。假设开关 S 打开直到它在时间 t = 0 关闭，然后保持关闭，产生“阶跃响应”类型的电压输入。电流 i 开始流过电路，但不会迅速上升到值 Imax，这由 V / R 的比率（欧姆定律）决定。
    该限制因素是由于磁通量增长导致电感器内存在自感电动势（楞次定律）。一段时间后，电压源抵消了自感应电动势的影响，电流变得恒定，感应电流和场减小到零。
    我们可以使用基尔霍夫电压定律 ( KVL ) 来定义电路周围存在的各个电压降，然后希望用它来为我们提供电流的表达式。

    基尔霍夫电压定律 (KVL) 告诉我们：

    基尔霍夫电压定律

    电阻R两端的电压降为I *R（欧姆定律）。

    电阻两端的电压降
    电感两端的压降L现在是我们熟悉的表达式L(di/dt)

    电感两端的电压降
    那么 LR 串联电路周围的各个电压降的终表达式可以给出为：

    lr串联电路电压
    我们可以看到，电阻两端的电压降取决于电流i，而电感两端的电压降取决于电流的变化率di/dt。当电流为零时，(  i = 0  ) 在时间t = 0上面的表达式，也是一阶微分方程，可以重写为给出任何时刻的电流值：

    LR 串联电路中电流的表达式

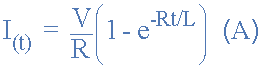
    通过 lr 串联电路的电流
    在哪里：
    V以伏特为单位
    R以欧姆为单位
    L在亨利
    t以秒为单位
    e是自然对数的底 = 2.71828
    LR 串联电路的时间常数(  τ  ) 由 L/R 给出，其中 V/R 表示经过五个时间常数值后的终稳态电流值。一旦电流达到5τ处的稳态值，线圈的电感就会降低到零，更像是短路，并有效地将其从电路中移除。
    因此，流过线圈的电流仅受线圈绕组的欧姆电阻元件限制。表示电路的电压/时间特性的电流增长的图形表示可以表示为。

    瞬态特性曲线
    lr 瞬态曲线
    由于电阻两端的电压降V R等于I*R（欧姆定律），因此它将具有与电流相同的指数增长和形状。然而，电感两端的电压降V L 的值将等于：   Ve (-Rt/L)。然后，电感两端的电压V L的初始值将等于时间t = 0或开关首次闭合时的电池电压，然后呈指数衰减至零，如上述曲线所示。
    流经 LR 串联电路的电流达到其稳态值所需的时间大约相当于5 个时间常数或5τ。这个时间常数τ由τ  = L/R测量，以秒为单位，其中R是以欧姆为单位的电阻值，L是以亨利为单位的电感值。这构成了 RL 充电电路的基础，其中5 τ也可以被认为是“ 5*(L/R) ”或电路的瞬态时间。
    任何电感电路的瞬态时间都由电感和电阻之间的关系决定。例如，对于固定值电阻，电感越大，瞬态时间越慢，因此 LR 串联电路的时间常数越长。同样，对于固定值电感，电阻值越小，瞬态时间越长。
    然而，对于固定值电感，通过增加电阻值，瞬态时间和电路的时间常数会因此变短。这是因为随着电阻的增加，电路变得越来越具有电阻性，因为电感的值与电阻相比变得可以忽略不计。如果与电感相比电阻值增加得足够大，则瞬态时间将有效地减少到几乎为零。
    教程示例 No1
    将一个电感为40mH、电阻为2Ω的线圈连接在一起，组成LR串联电路。如果它们连接到 20V 直流电源。
    A）。电流的终稳态值是多少。
    lr串联电路稳态电流
    b) RL 串联电路的时间常数是多少。
    lr串联电路的时间常数
    c) RL 串联电路的瞬态时间是多少。
    lr串联电路的瞬态时间
    d) 10ms 后感应电动势的值是多少。
    感应电动势
    e)开关闭合后电路电流常数的值是多少。
    瞬时电流
    电路的时间常数τ在问题 b) 中计算为20ms。那么此时的电路电流为：
    瞬时电流值
    您可能已经注意到问题(e)的答案在一个时间常数下给出的值为 6.32 安培，等于我们在问题 (a) 中计算的终稳态电流值 10 安培的 63.2 %。这个 63.2% 或 0.632 x I MAX的值也对应于上面显示的瞬态曲线。
    LR 串联电路中的电源
    然后从上面，电压源向电路供电的瞬时速率为：
    瞬时功率
    电阻以热的形式耗散功率的瞬时速率为：
    电阻中的功率
    能量以磁势能的形式存储在电感器中的速率为：
    电感功率
    然后我们可以通过乘以i找到 RL 串联电路中的总功率，因此：
    lr串联电路中的瞬时功率
    其中个I 2 R项表示电阻器以热形式耗散的功率，第二个项表示电感器吸收的功率，即其磁能。