正弦源
正弦电压源(从属或独立)产生的电压以正弦波的形式随时间变化。正弦电流源(从属或独立)产生的电流随时间变化。正弦变化函数可以用正弦函数或余弦函数表示。两者都同样有效;两种功能形式不能同时使用。在本文中使用余弦函数,正弦变化电压可以写成:
$$\textit{v}=V_{m}\cos(\omega\textit{t} + \phi )$$ (1.1)
为了帮助讨论正弦电压方程的参数,下面是电压与时间图的图 1.1

请注意,上面的正弦函数会定期连续重复。这种有规律的间隔函数称为周期性函数。一个关键参数是正弦函数通过其所有可能的值所需的时间长度。传递所有可能值所需的时间称为函数的周期,并表示为 T。正弦函数的周期以秒为单位。取 T 的倒数得到正弦函数的每秒周期数或频率,表示为 f,其中
$$\mathit{f}=\frac{1}{\mathit{T}}$$ (1.2)
每秒周期称为赫兹,或缩写为 Hz。在正弦电压方程中,系数 t 包含 T 或 f 的值。Omega ($$\omega $$) 表示正弦函数的角频率,其中
$$\omega =2\pi \mathit{f}=\frac{2\pi}{\mathit{T}} (\mathrm{弧度/秒}).$$ (1.3)
这个角频率方程基于这样一个事实,即余弦(或正弦)函数每次其参数 $$\omega \textit{t}$$ 通过 $$2\pi $$ rad $$(360^{\circ})$$时,余弦(或正弦)函数都会经过一组完整的值。每当 t 是 T 的整数倍时,参数 $$\omega \textit{t}$$ 就会增加 $$2\pi $$ rad 的整数倍。系数 $$V_{m}$$ 给出了正弦电压的幅度。因为余弦以 $$\pm 1$$ 为界,所以 $$\pm V_{m}$$ 以振幅为界。上图显示了这些特征。
方程 1.1 中的角度 $$\phi $$ 称为正弦电压的相位角。这个角度决定了 t = 0 时正弦函数的值;因此,它确定周期波上测量时间的起点。如果相位角 $$\phi $$ 发生变化,它会沿时间轴移动正弦函数,但不会改变振幅 $$(V_{m})$$ 或角频率 $$(\omega )$$。例如,将 $$\phi $$ 减少到零会将图 1.1 中所示的正弦电压函数向右移动 $$\frac{\phi }{\omega }$$ 时间单位,如图 1.1 所示。如果 $$\phi $$ 也是正的,则正弦电压函数向左移动,而如果 $$\phi $$ 为负,则电压函数向右移动。相位角 $$\omega \textit{t}$$ 和 $$\phi $$ 必须具有相同的单位,因为它们在正弦函数的参数中被加在一起。通常 $$\omega \textit{t}$$ 以弧度表示,但 $$\phi $$ 以度为单位,而 $$\omega \textit{t}$$ 在两个量相加之前从弧度转换为度数。从三角学中,从弧度到度数的转换由下式给出
$$\mathrm{(度数)}=\frac{180^{\circ}}{\pi }\mathrm{(弧度数)}$$ (1.4)
正弦电压(或电流)的另一个重要特性是其 rms 值。该值定义为平方函数平均值的平方根。从方程 1.1 中,$$\textit{v}$$ 的 rms 值为
$$\sqrt{\int_{t_{0}}^{t_{0}+T}V_{m}^{2}\cos ^{2}(\omega t + \phi )dt}$$ (1.5)
方程 1.5 中根式符号下的量减少为 $$\frac{V_{m}^{2}}{2}$$,得到 $$\textit{v}$$ 的值
$$V_{rms}=\frac{V_{m}}{\sqrt{2}}$$ (1.6)
这个正弦电压值仅取决于 $$\textit{v}$$ 的振幅,即 $$V_{m}$$。此外,rms 值不是频率或相位角的函数。
相量
相量是一个复数,它携带正弦函数的振幅和相位角信息。这个相量的概念植根于欧拉公式:
$$e^{j\theta }=\cos (\theta ) + j\sin (\theta )$$ (1.7)
这个方程很重要,因为它提供了另一种表示余弦和正弦函数的方法。余弦函数可以被认为是指数函数的实部,而正弦函数是指数函数的虚部;这将得到:
$$\cos (\theta )=\Re\left \{ e^{j\theta } \right \},$$ (1.8)
$$\sin (\theta )=\Im \left \{ e^{j\theta } \right \},$$ (1.9)
其中 $$\Re $$ 是“实部”,$$\Im $$is 是“虚部”。使用余弦函数分析正弦稳态以及指数函数的实部,正弦电压函数由下式给出:
$$v=V_{m}\cos (\omega t + \phi )$$
$$v=V_{m}\Re \left \{ e^{j(\omega t + \phi )} \right \}$$
$$v=V_{m}\Re \left \{ e^{j\omega t}e^{j\phi } \right \}$$ (1.10)
系数 $$V_{m}$$ 可以在函数的实部的参数内移动,而不会改变结果。反转参数内两个指数函数的顺序得到:
$$v=\Re \left \{ V_{m}e^{j\phi }e^{j\omega t} \right \}$$ (1.11)
在方程 1.11 中,量 $$V_{m}e^{j\phi }$$ 是一个复数,它包含给定正弦函数的振幅和相位角。这个复数也称为函数的相量变换。因此,相量变换由下式给出
$$\mathbf{V}=V_{m}e^{j\phi }=P\left \{ V_{m}\cos (\omega t + \phi ) \right \}$$ (1.12)
此相量变换将正弦函数从时域转移到复数域或频域。关于方程 1.12 还有一点要补充。指数函数 $$e^{j\phi }$$ 的周期性出现导致了一个缩写。这个缩写是角度表示法
$$1\angle \phi ^{\circ}=1e^{j\phi }$$ (1.13)
频域中的无源电路元件
首先,必须在无源电路元件
端子的相量电流和相量电压之间建立关系。其次,必须创建一个与 phasor 域有关的 Kirchhoff 定律版本。根据欧姆定律,如果
电阻器中的电流随时间呈正弦波变化,即 $$i=I_{m}\cos (\omega t + \phi ) $$ 电阻器端子处的电压为
$$v=RI_{m}[\cos (\omega t + \theta _{i})],$$ (1.14)
其中 $$I_{m}$$ 是电流的幅度是安培,$$\theta _{i}$$ 是电流的相位角。该电压的相量变换为
$$\mathbf{V}=RIe^{j\theta _{i}}=RI\angle \theta _{i}$$ (1.15)
但是 $$I_{m}\angle \theta _{i}$$ 是正弦电流的相量表示,因此方程 1.15 可以写成
$$\textbf{V}=R\textbf{I}$$ (1.16)
方程 1.16 是电阻器的相量电压和相量电流之间的关系,它指出电阻器端子处的相量电压就是电阻乘以相量电流。图 1.1 显示了频域中电阻器的电路图。
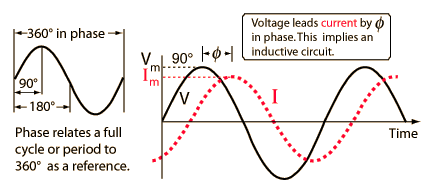
电感的 V-I 关系
电感器端子上的相量电流和相量之间的关系可以通过假设正弦电流并使用 $$L\frac{di}{dt}$$ 建立相应的电压来推导出来。因此,对于 $$i=I_{m}\cos (\omega t + \theta _{i}),$$ 电压的相量表示表达式为
$$\textbf{V}=j\omega L\textbf{I}$$ (1.17)
方程 1.17 表示电感器端子处的相量电压等于 $$j\omega L$$ 乘以相量电流。电感器端子两端的电压和电流正好异相 $$90^{\circ}$$。特别是,电压电流 $$90^{\circ}$$,或者等效地,电流落后于电压 $$90^{\circ}$$。这可以写成
$$\textbf{V}=\omega LI_{m}\angle (\theta _{i} + 90)^{\circ} $$ (1.18)
电容器的 V-I 关系
电容端子上的相量电流和相量电压之间的关系,由式 1.17 推导得出。请注意,对于电容器,
$$i=C\frac{dv}{dt},$$ 然后
$$\textbf{V}=\frac{1}{\textbf{j}\omega \textbf{C}}\textbf{I}$$ (1.19)
上式表示 capacitor 在 phasor 域中的等效电路。电容器端子两端的电压正好滞后于电流 $$90^{\circ}$$。这种关系由下式给出
$$\textbf{V}=\frac{I_{m}}{\omega C}\angle (\theta _{i} - 90)^{\circ}$$ (1.20)

图 1.3 显示了端子处电流和电压之间的相位关系 (\theta _{i}=60^{\circ})
阻抗和电抗
通过另一个重要的观察结果来结束对频域中无源电路元件的讨论。比较 Eqs。1.16、1.17 和 1.19 都是
$$\textbf{V}=Z\textbf{I}$$ (1.21)
在方程 1.21 中,Z 表示给定电路元件的阻抗。求解 Z,可以证明阻抗是电路元件的电压相量与其电流相量的比值。请注意,虽然阻抗是一个复数,但它不是相量。回想一下,相量是一个复数,显示为 $$e^{j\omega t}$$ 的系数
频域中的阻抗是类似于时域中的电阻、电感和电容的量。阻抗的虚部称为电抗。表 1.1 总结了每个元件值的阻抗和电抗值。
在频域中求解电路
在 t=0 时,幅度为 100 V 的 400 Hz 正弦电压施加在电感器的端子上。电感器中稳态电流的幅度为 20 A。
A) 电感电流的频率是多少?
电感中的电流频率也与电感端子两端的电压频率相同。因此,电感电流的频率为 400 Hz
B) 如果电压的相位角为零,则电流的相位角是多少?
电感电压的相位角:$$\phi _{v}=0^{\circ}$$
由于通过电感器的电流正好滞后于电压 $$90^{\circ}$$,因此电流的相位角为 $$\phi _{i}=-90^{\circ}$$
C) 电感的感抗是多少?
施加在电感器两端的电压的相量形式为 $$\textbf{V}=100\angle 0^{\circ} \mathrm{V}$$
电感器中电流的相量形式为 $$\textbf{I}=20\angle -90^{\circ}\mathrm{A}$$
确定电感的阻抗:
$$\mathbf{Z_{L}}=\mathbf{\frac{V}{I}}$$
$$=\frac{100\angle 0^{\circ}}{20\angle -90^{\circ}}$$
$$=5\angle 90^{\circ}$$
$$=j5\欧米茄 $$
电感器阻抗的表达式为:
$$\mathbf{Z_{L}}=jX_{L}$$
$$=j5\欧米茄 $$
因此,电感的感应电抗 $$X_{L}$$ 是 $$\mathbf{5\Omega }$$
D) 电感的电感值是多少(单位为毫亨利)?
电感的阻抗表达式为:
$$\mathbf{Z_{L}}=jX_{L}$$
$$=j\omega L$$
电感的表达式 L:
$$jX_{L}=j\omega L$$
$$L=\frac{X_{L}}{\omega }$$
将 $$5\Omega $$ 替换为 $$X_{L}$$,将 2513.27 rad/s 替换为 $$\omega$$:
$$L=\frac{5}{2513.27}$$
$$=1.99 \mathrm{ mH}$$
因此,电感器的电感量(以毫亨为单位)为 $$=1.99 \mathrm{ mH}$$
E) 电感的阻抗是多少?
$$\mathbf{Z_{L}}=j\omega L$$
$$=j(2513.27(1.99*10^{3})$$
$$=j5\欧米茄 $$
因此,电感的阻抗 $$Z_{L} \mathrm{ 为 } j5\Omega $$


