我们使用正在运行的 PSpice 电路示例(在我关于运算放大器频率补偿的文章中首次介绍)来比较去补偿与完全补偿:
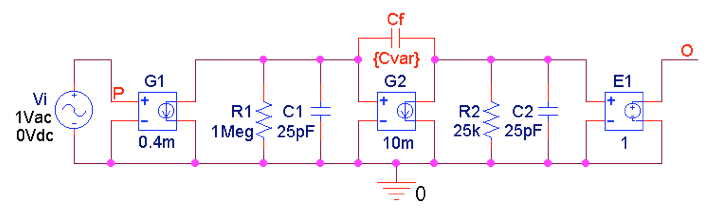
图 1.PSpice 电路绘制完全补偿和非补偿开环增益。
PSpice 的结果如下图所示:
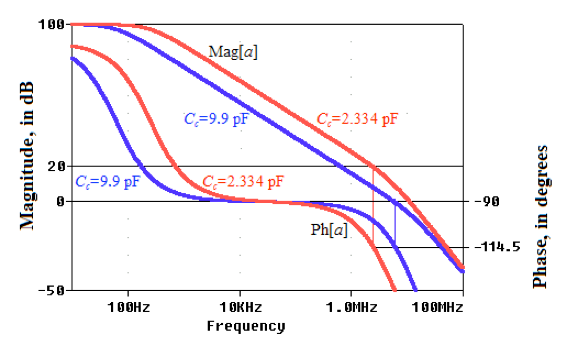
图 2.具有完全补偿的开环增益 (C= 9.90 pF,对于闭环增益 ≥ 0 dB) 和去补偿 (C= 2.334 pF,对于闭环增益 ≥ 20 dB)。两种补偿都享受m≥ 65.5°
结果得出以下观察结果:
全额赔偿 (C= 9.90 pF),则 0 dB 增益具有交越频率x≈ 5.86 MHz 和相位裕量m= 65.5°。此外,如果我们将完全补偿的运算放大器配置为 20 dB 闭环增益,则它具有x≈ 633 kHz 和m≈ 87°,比 0 dB 增益还要大。
失代偿 (C= 2.334 pF),则 20 dB 增益具有x≈ 2.37 MHz(带宽比完全补偿时更宽)并且仍然m= 65.5°。但是,如果我们将去补偿运算放大器配置为 0 dB 闭环增益,则x≈ 11.1 MHz 和m≈ 24°,裕量很差,因为去补偿器件的增益≥ 20 dB。跟m≈ 24°,20 dB 增益将表现出约 7% 的峰值和约 50% 的过冲瞬态响应,这两者通常是不可接受的。
现在让我们继续考虑如何使用外部因素在我们的电路中实现补偿;例如,电阻器。
使用电阻器进行外部补偿
尽管去补偿运算放大器适用于高于一个分钟 (一个分钟= 20 dB),其出色的动态特性使其也适用于增益低于一个分钟.
但这会降低相位裕量m,因此用户有责任对电路进行外部补偿,以保持m在所需的级别。
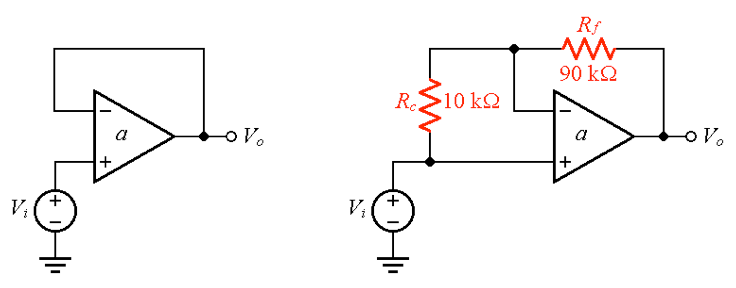
为了说明这一点,我们以图 1 中的去补偿形式的运算放大器为例,其中C= 2.334 pF,让我们将其配置为电压跟随器操作,如图 3(a) 所示。

(一) (二)
图 3.电压跟随器:(a) 未补偿,以及 (b) 外部补偿 m≈ 65.5°。
如前所述,该电路的相位裕量仅为m≈ 24°。我们如何将其提升为m= 65.5°一个简单的解决方案是将其 1/β 曲线提高到 20 dB,同时仍然确保单位增益。我们通过连接电阻对来实现这一目标Rc-R以 1 比 9 的比例,如图 3(b) 所示。→ ∞理想极限中的闭环增益仍然是
$$A_{理想}=1.0V/V$$
方程 1
(之所以如此,是因为 a → ∞运算放大器输入端子两端的电压趋于零。这意味着零电流通过Rc因此,零电流也通过R.因此,两端的电压R为零,因此我们有Vo = V我.)
或 1/β = 10 = 20 dB(请注意,1/β ≠一个理想在此示例中)。
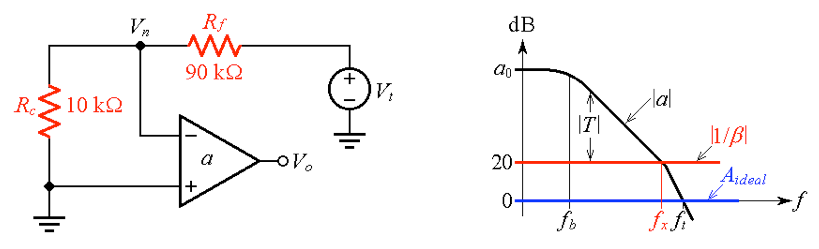
(一) (二)
图 4.(a) 电路求图 3(b) 和 (b) 波特图可视化的电压跟随器的反馈因子β。
响应如图 5 所示。
(一) (二)

图 5.(a) PSpice 电路,用于可视化 (b) 图 3 中电压跟随器的响应。拉普拉斯模块模拟了图 2 中的失代偿响应,使用 C= 2.334 pF 的
类似的推理思路适用于图 6(a) 的单位增益反相放大器。
(一) (二)

图 6.单位增益反相放大器的外部补偿。
在这种情况下,在 limit a → ∞ 中,我们有
通过检查,反馈系数现在是
$$β=\frac{R_{1}||R_{c}}{(R_{1}||R_{c})+R_{2}}=0.1$$
方程 4
在这种情况下,Rc已选中,以便使 (R1||Rc) = R2/9.
电阻补偿的应用(和缺点)
上述讨论专门用于单位增益同相和反相放大器,可以很容易地推广到除单位以外的闭环增益的情况,但仍然使 1 < (1 +R2/R1) < 一个分钟.
电路是否用作同相放大器 (一个理想= 1 +R2/R1) 或用作反相放大器 (一个理想= –R2/R1),只要条件 (1 +R2/R1) < 一个分钟holds,我们进行抵抗Rc在运算放大器的输入端子上,例如 1 +R2/(R1||Rc) = 1 +R2/R1 + R2/Rc = 一个分钟.
电阻补偿虽然简单,但有两个缺点:
可以使用与同相输入串联的电压源建模的任何噪声,例如输入偏移电压V操作系统,被放大 1/β,因此也称为噪声增益。
环路增益 T = (aβ = –Vo/Vt在图 4(a)) 中降低(在本例中为 10 倍),导致电路的闭环直流精度下降。
输入滞后补偿
我们可以通过放置合适的电容来减轻电阻补偿的局限性Cc与Rc,如图 7(a) 所示的反相放大器。
(一) (二)

图 7.(a) 单位增益反相放大器的输入滞后补偿,以及 (b) 波特图可视化。
请注意,为了确保所需的相位裕量,我们只需要在交越频率附近将放大器欺骗到所需的收盘率 (ROC)x,不一定一直到 DC。
从物理上讲,1/β 曲线在频率c其中电容阻抗的大小等于Rc或 |1/(j2πCc|=Rc给
$$C_{c}=\frac{1}{2π R_{c}f_{c}}$$
方程 5
防止相裕量明显腐蚀m,习惯上将c大约低于十年x或
对于图 7(a) 所示的电路,这意味着Cc≈ 54 pF。图 8 的模拟得出的测量值为x= 2.38 MHz 且m= 61°。
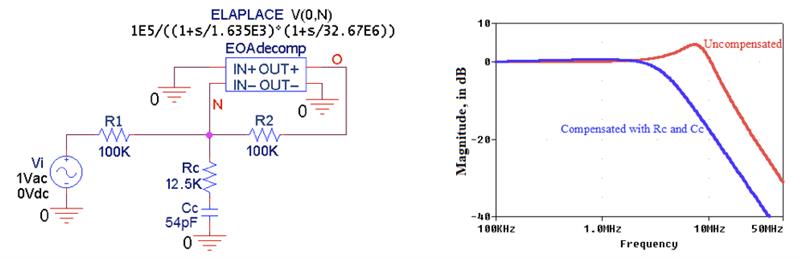
图 8.(a) PSpice 电路,用于 (b) 可视化单位增益反相放大器的输入滞后补偿的稳定效果。
外部频率补偿的另一种方法
众所周知,输入滞后补偿会在闭环响应中产生极点零双峰,这会导致难以忍受的长建立时间特性。Michael Steffes 提出的替代补偿方法避免了这些缺点,如图 9 所示。
(一) (二)
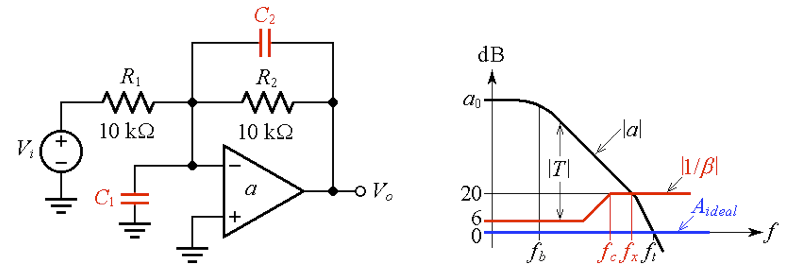
图 9.(a) Michael Steffes 的去补偿运算放大器补偿技术,以及 (b) 波特图可视化。
我们在上一篇文章中已经遇到过这种类型的 circuit stray input capacitance compensation,因此其中的许多考虑也适用于当前的电路,的区别是现在C1是有意为之的。
我们有兴趣开发两个条件来指定C1和C2.在高频下,其中C1和C2的星等比R1和R2,我们可以忽略R1和R2并说明在高频下我们有 1/β → 1 +C1/C2.
拼版 1 +C1/C2= 20 dB = 10 给出了我们电路示例的个条件
第二个条件源于以下事实:
$$C_{2}=\frac{1}{2π R_{2}f_{c}}$$
方程 8
因此,的C2取决于我们决定的定位c.
这里我们没有应用 Steffes 的详细分析(这超出了本文的范围),而是采用启发式方法。
我们从公式 (6) 和 (8) 开始,使用图 10 的 PSpice 电路来观察我们逐渐增加时的交流响应c通过递减C2同时保持方程 (7) 的条件。
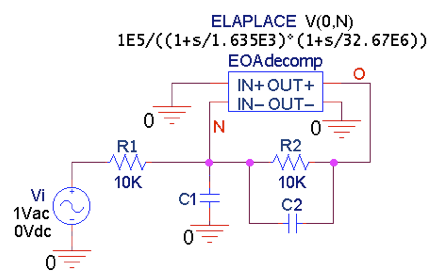
图 10.PSpice 电路绘制图 9a 中反相放大器的交流响应。要绘制瞬态响应,请将 AC input 源更改为脉冲源。
当 AC 响应刚开始出现峰值时,我们停止。这种方法提供了C2= 12 pF 且C1= 9C2 = 108 pF,从而产生图 11 中表现良好的响应。交流响应的 –3 dB 频率为 2.36 MHz。
(一) (二)
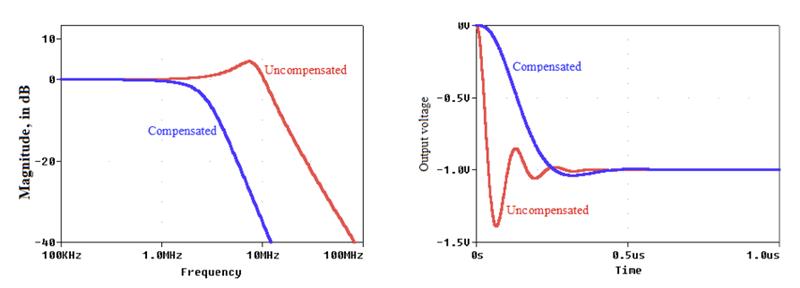
图 11. 图 10 中反相放大器的 (a) 交流响应和 (b) 阶跃响应。
值得指出的是,任何杂散电容Cn可以通过更改C1自9C2–Cn.所以,如果,比如说,Cn= 20 pF,则我们使用C1= 88 pF 的











