量子力学的有序世界从根本上来说是基于线性算子理论的。各个物理量(能量、冲量、角动量等)由作用于希尔伯特空间(欧几里得空间的复数等价物)中振荡的函数的算子来表示。这种范式使得我们所目睹的
半导体器件(近年来的 SiC 和 GaN)的快速发展成为可能。然而,有相当多的物理学家将线性解释为非线性理论的近似过程的结果。在本期中,我们将研究非线性薛定谔型微分方程引起的影响。
与 Mathematica 的数值集成 这里我们指的不是稳态薛定谔方程,而是与时间相关的方程(波动方程),在我们打算研究的情况下,它是一个非线性偏微分方程(PDE)。这类方程很难解析求解,因此我们采用数值分析。此外,在线性情况下也会出现困难,例如产生布洛赫波的周期性势。
我们的攻击策略包括编写一个方程,其中非线性项由系数β控制。因此,我们从β = 0开始,推导出 Bloch 数据包的动态演化。下一步需要β的非零值。计算负荷不仅取决于非线性项,还取决于周期性电势(顺便说一句,在零电势的情况下,可以解析求解非线性方程。
因此,必须添加周期势作为“弱扰动”;从物理上讲,这意味着我们处于弱键近似,这是金属行为的特征。图 1 显示了找到解决方案的时间顺序。不应解释纵坐标上的值,因为为了避免舍入误差,我们已经对方程中出现的物理常数(约简普朗克常数和电子质量)进行了归一化。初始脉冲是极其局部化的,之后它趋于变宽,这正是色散现象所预期的。
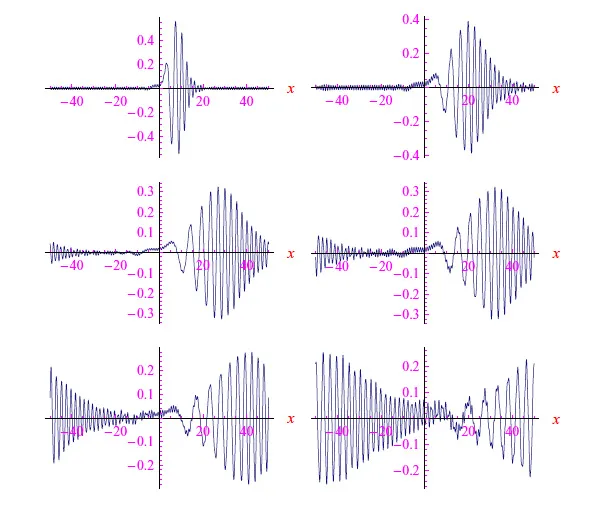
图 1:布洛赫波包的时间演化。
在第三帧中,局部振荡出现在与数据包的区域不相交的区域中,该区域逐渐增强,从而产生第二个数据包(第五帧和第六帧)。电子似乎分裂成位于各个数据包中的两个“版本”。如前一期所示,布洛赫包可简化为由与晶格具有相同周期性的函数调制幅度的德布罗意包。因此,电子不会分裂,我们只是以相同的概率在分配两个数据包的区域中找到它:因此,我们处于隧道过程中。
现在让我们考虑β > 0,这相当于在薛定谔方程中引入非线性项。图 2 是在给定时刻t > 0 且x从 -50 变化到 +50(采用通常的无量纲单位)以增加β值时解的演化序列。当β = 0 时,方程是线性的,解绘制在张图中。这是布洛赫波包的典型行为。
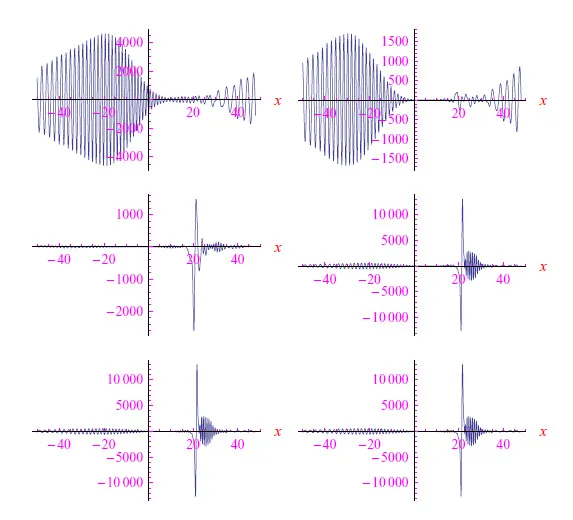
图 2:孤子的形成。在(无量纲)时间t = 20,随着β值的增加,布洛赫包塌陷为孤子
我们看到,在x =20(无量纲单位)的邻域中找到电子的可能性很大,而且在x = 40的邻域中也有很大的概率。没什么奇怪的,这就是隧道效应。在第二张图中,[?5 , 15]中的振荡趋于减弱。在下图中,我们看到电子实际上位于x = 20 处,除了剩余的振幅可以忽略不计的振荡之外。像往常一样,我们不需要解释纵坐标的值,因为我们有无量纲的薛定谔方程。
结论
结论部分是一组问题。我们首先观察到系数β可能取决于晶格的热力学平衡温度T。众所周知,超导性是在临界温度T c下发生的相变。因此,我们推测当T > T c时, β = 0 。相反,当T < T c时,会出现非线性效应,如上一节所示,会产生孤子。
孤子的基本特征是它们不表现出德布罗意/布洛赫波包所特有的色散和展宽效应,其中电子位置测量的不确定性随着时间而增加。我们顺便注意到,在信息论的范式中,波包的展宽可以通过信息的丢失来解释,因此也可以通过香农意义上的熵的丢失来解释2。
那么我们能否将这种扩大与热力学意义上的熵增加联系起来呢?如果我们考虑一组孤子型系统的统计数据,答案是肯定的。从宏观电子数量来看,金属也是如此。我们认为这种解释很有趣,因为根据 BCS 模型 3,超导是典型的玻色-爱因斯坦型相变过程。众所周知,这种过程是低熵的;在超导的情况下,由于焦耳效应,不存在散热。因此,我们的想法(远非结论性的)是,我们认为超导性的波解释是有用的,因为这可以推广到其他领域,例如涉及生命物质的物理过程,其特征是具有降低熵值的能力。

