线性系统的重要性
工程师对属于“线性”类别的系统特别感兴趣。我们拥有强大的数学工具,可以帮助我们分析线性且时不变的系统,并且许多物理现象可以地建模为线性系统——尽管当我们考虑所有细节时,这些现象通常不是完全线性的。
在电路设计中,我们经常追求线性度,因为它可以带来理想的输出特性。例如,线性音频放大器产生失真较小的声音,而射频信号链中的线性操作有助于接收器正确解码正交调幅 (QAM) 波形。
线性是信号处理应用中数学分析和操作的关键:叠加的概念是数字信号处理的基础,叠加仅适用于我们使用线性系统的情况。
线性系统的要求
为了确定系统是否是线性的,我们需要回答以下问题:当输入信号应用于系统时,输出响应是否表现出同质性和可加性?如果一个系统既是齐次的又是可加的,那么它就是线性系统。
均匀性
假设我们将输入信号 x(t) 应用到系统,它会产生输出信号 y(t)。然后,我们应用信号 kx(t),其中 k 是常数。如果系统是线性的,则新的输出信号将为ky(t)。如果对于任何输入信号和任何常数都发生同样的情况,则系统表现出同质性。
同质性原理也称为标量规则或标度特性。基本思想是缩放输入信号(即乘以一个常数)将以相同的方式缩放输出。
让我们考虑一个 RC 低通滤波器。输出信号的幅度取决于输入信号的频率,但无论频率如何,缩放输入信号始终会导致输出信号的相等缩放。您可以将输入信号乘以任何因子,输出信号也将乘以相同的因子。因此,该系统是同构的。
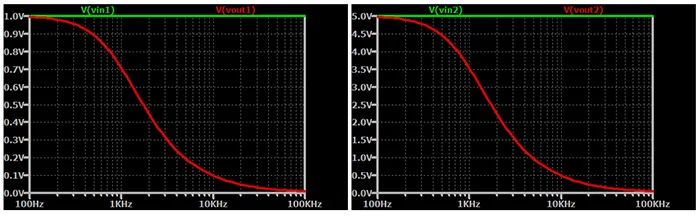
低通滤波器是一个线性系统,其输出响应与输入信号成比例。
现在让我们想象我们的系统是一个电阻加热器。输入信号 x(t) 是电流源产生的电流,输出信号 y(t) 是电阻元件产生的热量。以热量形式耗散的功率与流经电阻器的电流量的平方成正比。因此,如果我们将电流增加十倍(即 k = 10),输出就会增加一百倍。在这种情况下,kx(t) ≠ ky(t),并且系统不是齐次的。
电阻加热器的例子很有趣,因为我认为我们大多数人都会自然地将电阻器识别为线性元件。但实际上元件本身并不是线性的,而是电压和电流之间的关系(我们称之为欧姆定律)是线性的。当我们对电流和功率(或电压和功率)之间的关系感兴趣时,电阻器是一个非线性系统。
可加性
如果传送到加法系统的输入是通过添加单独的信号而创建的复合信号,则输出也将是包含这些添加的信号的修改版本的复合信号。另一种思考方式是,系统将求和之前的信号视为独立的信号,尽管事实上它们是作为一个信号传递和处理的。
通过数学可能更容易解释可加性。假设输入信号x 1 (t)和x 2 (t)产生输出信号y 1 (t)和y 2 (t)。现在,我们通过添加原始的两个输入信号来创建复合信号 x C (t):x C (t) = x 1 (t) + x 2 (t)。在加法系统中,如果输入为 x C (t),则输出 y C (t) 为两个原始输出信号之和:y C (t) = y 1 (t) + y 2 (t)。
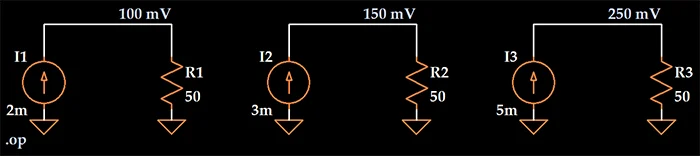
假设我们的系统是一个 50 Ω 电阻;输入信号是电流,输出信号是电压。如果输入为 2 mA,则输出为 100 mV。如果输入为 3 mA,则输出为 150 mV。如果输入为 5 mA (= 2 mA + 3 mA),则输出为 250 mV (= 100 mV + 150 mV)。因此,该系统是可加的。
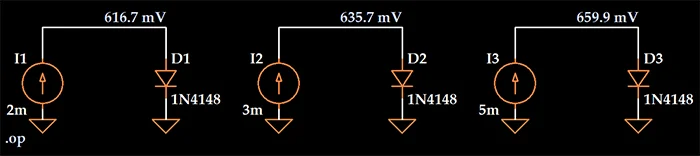
现在让我们通过二极管而不是电阻来驱动输入信号。下面显示的 LTspice 结果表明,当输入信号是电流且输出信号是电压时,二极管不是加性系统。
结论
我们已经看到线性是工程系统的一个重要特征,并且我们已经研究了区分线性系统和非线性系统的两个属性。然而,为了更彻底地探讨这个主题,我们需要涵盖更多概念;为此,我们将在以后的文章中讨论时间不变性(也称为平移不变性)、脉冲响应、静态线性度和正弦保真度。


