重要的是要了解有源滤波器本质上并不比无源滤波器“更好”。相反,我更喜欢无源滤波器并尽可能使用它们。老式方法的一些优点如下:
无需担心
运算放大器的非理想特性——失调电压、带宽限制、噪声。 。 。 。
试验板或 PCB 布局更加简单、干净,无需运算放大器所需的电源和接地连接。
无源电路更加简单,因此较少出现设计错误,例如,将
电阻器-电感器-
电容器 (RLC) 低通滤波器(参见下一节)与等效的 Sallen-Key 电路进行比较(向下滚动到“Sallen” –关键”部分)。
有源滤波器当然有其优点。适用于一阶和二阶滤波器的突出的优点是改进的阻抗特性。运算放大器提供高输入阻抗和低输出阻抗,因此当输入信号具有相对较高的源阻抗或输出信号必须驱动相对较低的负载阻抗时,基于运算放大器的有源滤波器可以优于无源实现。
另一个优点是增益:如果信号不仅需要滤波还需要放大,那么您实际上别无选择,只能使用有源滤波器 - 特定的有源滤波器拓扑或无源滤波器加放大器布置。
在继续之前,我应该指出,当然可以创建一个由一个运算放大器和两个一阶滤波器组成的二阶有源滤波器。两个滤波器级串联连接,运算放大器缓冲级的输出。这些“级联”滤波器不可避免地会产生从通带到阻带的逐渐过渡,从而导致非线性相位响应以及通带末端附近信号的显着衰减。下面讨论的两种二阶拓扑通常更可取,因为它们允许您优化单个电路,以实现从通带到阻带的更锐利的过渡、的通带衰减或线性相位响应。
邪恶的电感器
正如其标题所示,本文重点关注二阶有源滤波器,即传递函数具有两个极点并因此实现更陡峭滚降的滤波器。无源滤波器需要两个能量存储元件(电容器和电感器)来提供二阶响应。 。 。这就是麻烦开始的地方。这是二阶 RLC 低通滤波器,其截止频率 (f c ) 和品质因数 (Q) 的方程式为:
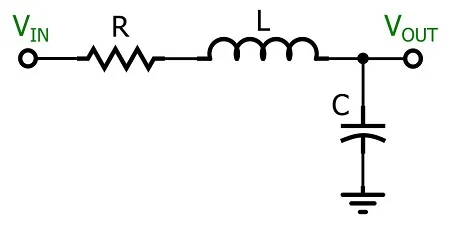
fc=12π√LC Q=(2πfc)×CR 这个本来很受人尊敬的滤波器因其与电感器的关联而受到污染。事实上,电感器非常不受欢迎,原因如下:
它们体积庞大,您可能已经注意到,
电子制造商希望将他们的小部件做得更小,而不是更大。
电感器与
集成电路制造技术并不是特别兼容:
IC 电感器无法获得太大的电感,这意味着滤波器的截止频率不能太低。
IC电感严重不理想; IC 环境的各种寄生阻抗比分立电感器所经历的问题更严重。
电感器比电阻器和电容器产生更多的电磁干扰 (EMI),并且也更容易受到 EMI 的影响。
电感器与主导电子行业的趋势(小型化、单片制造、无线功能)之间的明显冲突是追求不需要电感的二阶滤波器的主要动机。
安东尼奥和他的模拟电感器
避免与电感器相关的问题的一种方法是使用行为类似于电感器但仅需要电阻器、电容器和运算放大器的电路。以下“电感模拟电路”是由 Andreas Antoniou 发明的:
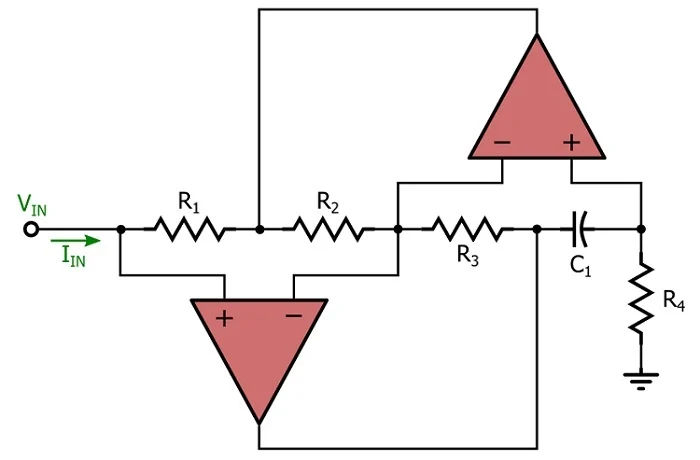
等效\电感: L=R1R3R4C1R2
我无法理解安东尼奥教授是如何弄清楚这一点的。无论如何,我不会详细讨论这个电路,因为Sallen-Key和多反馈(MFB) 拓扑是实现二阶滤波器性能的更简单、更直接的途径。不过,值得注意的是,通过使用电感模拟电路,可以在没有电感器的情况下实现各种 RLC 滤波器。
萨伦-基
Sallen-Key 滤波器为您提供两个极点,只需一个运算放大器和一些无源器件。以下是单位增益低通滤波器的 Sallen-Key 实现。
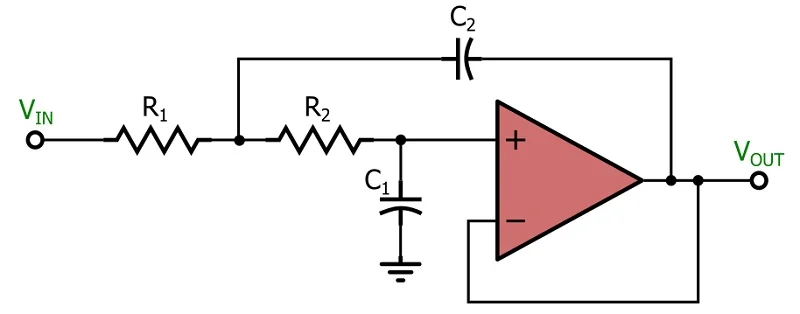
fc=12π√R1C1R2C2
通常情况下,不需要放大输入信号的任何部分;滤波器的作用是抑制不需要的频率,如果感兴趣的频率只是通过也没关系。这些单位增益应用非常常见,足以使 Sallen–Key 成为非常流行的滤波器,尽管事实上当增益明显高于单位增益时 MFB 拓扑具有优势。
让我们考虑一下低频时会发生什么。 C 1和C 2变为开路,并且电阻器变得无关紧要,因为流入运算放大器正输入端子的电流可以忽略不计。因此,我们只剩下一个电压跟随器。这意味着 1) Sallen-Key 滤波器不会反转信号,2) 增益几乎完全一致,不依赖于元件值。正如您将在下一节中看到的,MFB 电路的增益由元件值决定,即使在单位增益下也是如此,这解释了为什么 Sallen-Key 拓扑是单位增益应用的。
有关 Sallen–Key 拓扑的更多信息,请单击此处 (PDF) 查看德州仪器 (TI) 的应用说明,该说明可能会告诉您有关基于运算放大器的有源滤波器的所有您想了解的信息。另一个有价值的资源是这个在线滤波器设计工具,它将帮助您使用 Sallen–Key 低通和高通电路。
多重反馈
这是一个 MFB 低通电路:
fc=12π√R2R3C1C2
DC\增益 = R3R1
如果用开路替换电容器并忽略 R 2(同样,因为输入电流可以忽略不计),您将识别标准运算放大器反相配置:
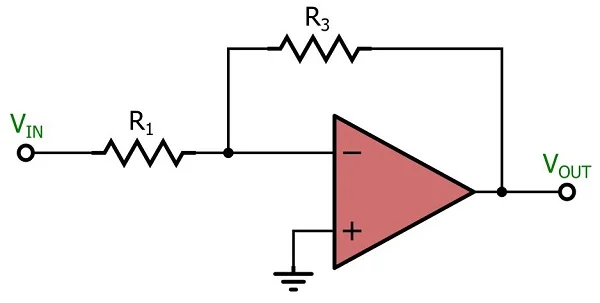
因此,MFB 是一种反相拓扑。您可能还记得,电压跟随器没有反相版本;而是没有反相版本。如果您需要单位增益反相运算放大器电路,则必须使用 R 1 = R 3的反相放大器。这同样适用于 MFB 拓扑:对于单位增益,您设置 R 1 = R 3,这意味着增益的精度取决于电阻器的精度。然而,随着增益的增加,MFB 电路实际上对元件容差的敏感度低于等效的 Sallen-Key 实现,因此 MFB 通常是更高增益滤波器的更好选择。上一节中提到的应用笔记也是 MFB 电路的重要资源,同样的在线滤波器工具可以帮助您进行 MFB 滤波器设计。



