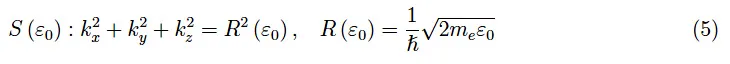在上一期中,我们看到在索末菲模型中,金属的传导电子的能量ε接近费米能量ε F。由于这是一个半经典模型,参考费米速度 vF 和相对轨迹(绕过海森堡测不准原理)是合理的。换句话说,在上述模型中,量子效应被纳入费米-狄拉克统计分布中,而不是单个电子的动力学中。因此称为半经典模型。
我们将 e 表示为动量(或冲量)p = m e v 的函数:

由此,费米冲量被定义:

下一步是应用德布罗意的假设(旧量子理论):与电子相关的物质波是具有传播矢量的平面波:

等式(1)变为:

这又将单个电子的能量表示为德布罗意波传播矢量的笛卡尔分量的函数。因此,我们有一个由三个实变量组成的实函数,其图形在 R 4中(无法可视化)。然而,我们可以追踪上述函数的水平面,称为等能面。更准确地说,如果ε 0是能量的允许值,则相应的等能面为:
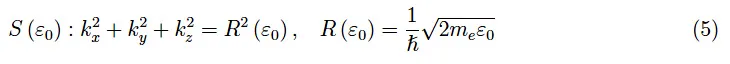
即,以 k 空间(三维欧几里得)原点为中心、半径为R ( ε 0 ) 的球体。特别地,费米球是表面S ( ε F )。具备量子素养的读者可以识别波数 k = |k|作为一个“好量子数”,k地定义了单个电子的量子态,专门参考了统计分布并从自旋中抽象出来。ε的定义源自对k 的函数依赖性,如方程 (4) 所示。
由于e 通过其模量取决于k ,因此 k 空间中能量ε的分布是各向同性的,因此相应等能表面(球体)的点代表物理上不同的状态,但具有相同的能量。在量子力学中,这通过断言能级ε是无限简并度的简并来表达。更准确地说, 2,即等于前述表面的点数。然而,我们必须考虑旋转的自由度。一般来说,自旋引起的简并度写为g s = 2 s + 1,其中s是所考虑粒子的自旋。对于电子,s = 1 / 2,因此g s?? = 2;事实上,任何自旋为 1 / 2 的状态k(即,被自旋向上的电子占据)都不同于具有相同波数k但自旋为1 /2 (自旋向下)的状态。
两种状态具有相同的能量;因此附加的简并度等于 2。请注意,由于上述状态在物理上是不同的,因此并未违反泡利不相容原理。由于它们有无限多个,每个电子都被一对分别向上和向下自旋的电子占据,因此可以考虑实际上无限数量的电子,这些电子与所考虑的晶体的理论上无限延伸相兼容(因此不破坏晶格的周期性)。
根据索末菲模型,对金属导电性有贡献的电子是那些状态“分配”在 k 空间费米球上的电子。这些状态的分布是各向同性的,因此对于替换 k -> – k 是对称的。由于 k 通过方程(3)与单个电子的动量 p 相关,因此总动量为零,电流(电流密度)也将为零。施加均匀静电场 E,转化为作用在单个电子上的恒定力 F = e E。
根据动量定理,电子动量随时间的变化δt为δ p = F δt,其对应于等式(3)中的δ k。由此可见,电场的作用在于将费米球转化为k空间。这破坏了各向同性,从而破坏了 k 和 k 之间的对称性。结果是非零的总动量,因此是净电荷流。电场的瞬时关闭重建了初始配置(没有电流),将费米球的中心移动到 k 空间坐标系的原点。这几乎是通过涉及电子晶格碰撞的统计机制立即发生的。
金属中的回旋共振
在之前的教程中,我们看到,在半导体中,通过测量平行于 B 0传播的平坦单色电磁波的吸收,可以测量由应用均匀静磁场 B 0产生的回旋加速器频率ω c 。对于金属,由于以下原因,该技术难以实施:
金属几乎完全反射电磁波,除非我们使用频率ω > ω p ,其中ω p 是等离子体频率,与传导电子1数量的密度 n 成正比。由于对于金属n 的量级为10 23 cm -3,因此我们有10 16 rad/ s量级的ω p ,其对应于频率f p约为10 4 GHZ
频率ω > ω p的电磁波的穿透深度δ相对较低(集肤效应)。对于频率f = 1 GHz,d的典型值约为10 -5 cm;δ识别给定金属,即所谓的皮肤区域
如前所述,大多数金属的费米面与球形不同。这破坏了单电子能量分布作为 k 函数的各向同性。由此可见,通过改变B 0的方向,可以获得不同的回旋频率
一些俄罗斯物理学家测试的技术包括使用一块金属板,该金属板受到平行于板平面的磁场 B0 的影响。这样,单个电子的轨迹轴就包含在上述平面内。
符号:该技术的一个变体由 Azbel-Kaner 几何给出2
射频场垂直于B 0发送。如果R 0 > δ,其中R 0是单个回旋加速器轨道的半径,则只有一部分轨道将受到电磁场的影响。然而,穿过皮肤区域的电子可以吸收电磁场的能量,从而加速。在相反的情况下(即,如果它向场释放能量),它会减速。类似的机制也发生在回旋加速器(粒子加速器)中;因此,量ω c 被称为回旋频率,在电磁学论文中被称为拉莫尔频率。
因此,我们预计会出现吸收峰(共振),但在电子向射频场释放能量的情况下也是如此。准确地说,电子的周期运动在与B 0正交的平面上的投影必须与电磁场同相。如果上述运动的周期为T c = 2 π/ω c ,电磁场的周期为T = 2 π/ω ,则T c = nT ,其中n为正整数。回顾回旋频率ω c的表达式,我们得到共振条件:

返回电子与射频场共振的静磁场B 0的值。对于费米面近似为球形的碱金属,在n> 1的不同值下测量B 0的值,由此从等式(6)获得有效质量,然后对所获得的结果进行平均。对于氦温度下的铜,请参阅参考资料。
结论
回旋共振实验不仅使我们能够确定金属和半导体中载流子的有效质量,而且还为研究费米表面的拓扑结构提供了一个极好的工具。