调节
变压器电压
对于单相变压器,电压调节可以定义为在零负载和变化负载条件下,次级
端子电压与其初始电压相比的百分比变化。调节决定了由于连接到变压器的负载的变化而在给定变压器内部发生的次级端电压变化 ,并且如果损耗较高则影响其效率和性能,从而降低次级电压。
变压器电压调整率可以使用以下公式计算为函数变化:
\[调节=\frac{输出\,电压\,变化}{空载\,输出\,电压}\]
\[调节=\frac{V_{空载}-V_{满载}}{V_{空载}}\]
根据上式,变压器的电压调整率可以用两种方式定义:
电压调节下降,Reg down:当负载连接到变压器次级端子并且该端子输出的电压下降时,就会发生这种情况。
电压调节,Reg up:当变压器次级端子处的负载被移除且端子处的电压上升时,就会发生这种情况。
这里变压器的电压调整率由所使用的参考电压决定,该参考电压是空载还是负载。
根据上面的等式,我们可以使用以下公式计算变压器的百分位电压调整率:
\[\%Reg_{down}=\frac{V_{空载}-V_{满载}}{V_{空载}}\times100\%\]
\[\%Reg_{up}=\frac{V_{空载}-V_{满载}}{V_{满载}}\times100\%\]
问题1
某变压器空载开路电压为120V,加负载时电压降至110V。计算变压器的电压调整率百分比。
解决方案
\[\%Reg_{down}=\frac{V_{空载}-V_{满载}}{V_{空载}}\times100\%\]
\[\%Reg_{向下}=\frac{120-110}{120}\times100\%=8.33\%\]
问题2
具有 5% 电压调整率的单相变压器满载时次级端子电压为 115.5 伏。如果负载被移除,则计算变压器的空载端子。
解决方案
\[\%Reg_{up}=\frac{V_{空载}-V_{满载}}{V_{满载}}\times100\%\]
\[5\%=\frac{V_{空载}-115.5}{115.5}\times100\% \]
\[V_{空载}=115.5+115.5\次\frac{5}{100}=121.275V\]
从计算中注意到,连接到变压器的负载的变化会引起变压器的端电压在满载和空载电压之间变化,这使得变压器的电压调节成为给定变压器的外部功能。因此,为了使变压器更加稳定,电压调节量应该很小。为了实现这一点,连接的负载应该具有更大的电阻。
我们来看看为什么变压器二次端电压会随着负载电流的变化而变化。
带载时的变压器
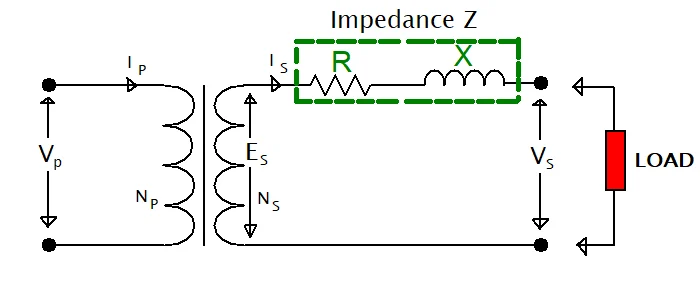
图 1.负载变压器。
通过次级绕组向负载供电的变压器会因叠片铁芯上产生的
磁铁损耗和因绕组电阻而产生的铜损耗而产生损耗。相反的力将电阻和电抗注入变压器的绕组中,形成一个阻抗通道,次级 I 端子处的电流输出必须流过该阻抗通道 。
从上图中可以看出,次级绕组由电抗和电阻组成。电抗和电阻会导致变压器绕组中产生电压降,电压降取决于所提供的负载电流和次级绕组的有效阻抗。
欧姆定律指出
\[V=IZ\]
这解释了次级绕组电流的增加导致变压器绕组中的电压降的增加。
次级绕组的阻抗是通过漏电抗 X 和电阻 R 的相量之和来计算的,其中每个参数都会产生不同的电压。
因此,次级阻抗由下式确定:
\[阻抗,Z=\sqrt{R^{2}+X^{2}}\]
无负载时的次级电压可由下式确定:
\[V_{S(空载)}=E_{S}\]
满载时,次级绕组电压可计算为
\[V_{S(满载)}=E_{S}-I_{S}R-I_{S}X\]
或者
\[V_{S(满载)}=E_{S}-I_{S}(R+jX)\]
所以,
\[V_{S(满载)}=E_{S}-I_{S}Z\]
从上面的方程可以明显看出,变压器的绕组由与电抗串联的电阻组成,并且负载电流对于这两个参数保持相同。对于电阻,电流和电压同相,并且由 I S R 确定的电阻两端的电压降应与由 I S确定的变压器次级电流同相。
对于
电感器,变压器中的电流滞后 90 度,
电感器两端的电压由 I S X 和相量角 φ L确定。
相量角可由下式计算:
\[cosφ_{R}=\frac{R}{Z}\]
重新排列
\[R=Zcosφ_{R}\]
和
\[sinφ_{X}=\frac{X}{Z}\]
所以,
\[X=Zsinφ_{X}\]
\[Zcosφ=Z(cosφ_{R}\times cosφ_{X}+sinφ_{R}+sinφ_{X})\]
关于简化:
\[Zcosφ=Rcosφ+Xsinφ\]
由于 V=IZ,变压器次级阻抗上的电压降可以求解为
\[V_{drop}=L_{S}(Rcosφ+Xsinφ)\]
对于滞后功率因数,表达式如下
\[V_{S(满载)}=V_{S(空载)}-V_{下降}\]
\[V_{S(空载)}=V_{S(满载)}+I_{S}(Rcosφ+Xsinφ)\]
\[\%Reg.=\frac{I_{S}(Rcosφ+Xsinφ)}{V_{s(空载)}}\times100\%\]
变压器的次级输出电压随着正弦和余弦之间的正电压调节而降低,从而导致功率因数滞后。滞后功率因数源自感性负载。
变压器的次级输出电压随着正弦和余弦之间的负电压调节而增加,从而产生超前功率因数。超前功率因数源自容性负载。
它违背了滞后和超前负载的调节表达式保持相同并且仅符号改变以指示下降或上升的逻辑。
因此,超前功率因数的调节表达式为:
\[\%Reg.=\frac{I_{S}(Rcosφ-Xsinφ)}{V_{s(空载)}}\times100\%\]
问题3
额定功率为10KVA的单相变压器提供空载110V二次电压。其次级绕组电阻为 0.015 欧姆,电抗为 0.04 欧姆。考虑到滞后功率因数为 0.85,计算变换电压调整率。
解决方案
\[cosφ=0.85\]
\[φ=cos^{-1}(0.85)=31.8°\]
所以,
\[sinφ=sin\,sin\,31.8=0.527\]
次级电流计算如下
\[I_{S}=\frac{VA}{V}=\frac{10000}{110}=90.9\]
% 电压调节率可计算为
\[\%Reg.=\frac{I_{S}(Rcosφ-Xsinφ)}{V_{s(空载)}}\times100\%\]
\[\%Reg=\frac{90.9[(0.015\times0.85)+(0.04\times0.527)]}{100}\times100\%=2.8\%\]
