1显示了需要调节 LM350(LM317)可调稳压器的输出电压时的典型使用方法。
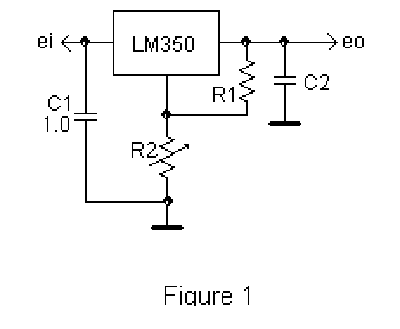
该电压大致如下:
eo = Vref * (R2/R1 + 1)
电位器 R2 通常是电路中不可靠的部分。如上式所示,电位器故障(例如,接触不良、断路)会使 R2 的有效值达到值,从而使输出电压也达到值 — 仅比输入电压低约 1.5 V。
当调整次数很少且负载的安全性并不重要时,这可能不是一个很大的问题。但是,当您想要频繁调整,或者事先不知道负载时(例如实验室电源的情况),图 2a中的电路可能是更好的选择。
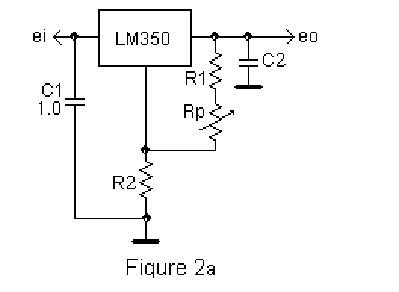
但是,该电路无法将其输出电压调节至下限Vref;这是它的局限性。
有几种安全可调稳压器的替代配置,或多或少可以避免过度使用带来的危险。安全的情况是输出电压非常接近 Vref,需要 3 或 4 个额外部件(即电阻器和晶体管);因此,让我们看看图 2b中更具妥协性的配置。
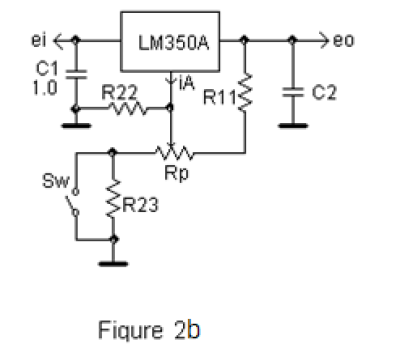
此电路可以调节输出电压至下限 Vref。输出电压(如果电位器 Rp 发生故障)约为 2…5 伏,这是一个折衷方案。
由于图2c中的电路计算不是很简单,因此这里将以Python代码的形式提供一些计算路径。
该电路具有两个输出电压范围:eo11 至 eo12 和 eo21 至 eo22(见代码)。范围由
开关 Sw(例如 nJFET、nFET 或任何良好的机械簧片
继电器)选择。
请注意:如果电阻器 R11 和 Rp 太大,无法提供稳压器 IC 所需的负载( 10 mA),则如果总负载太轻,输出可能会失控。
为了避免这种情况,开始计算并选择 R11 的任何适当值可能是更明智的做法。
您还必须提供 Rp 和范围的值。
此代码计算 R22 和 R23:
#-代码开始
R11=560 # 欧姆
Rpot=2180 # 欧姆
eo11=1.25 #V
eo12=5.6 #V
eo21=5.4 #V
eo22=23.0 #V
Vref=1.25 #V
打印()
# 设
K12 = eo12/Vref – 1
K21 = eo21/Vref – 1
K22 = eo22/Vref – 1
Rp = Rpot
从数学导入 sqrt
def checkEq(R11, R22, R23):
Rx=R11 – Ra/K12
如果 Rx != 0: print(“Err R11:”, Rx)
Rx=R22*R23/(R22+R23) – K21*(Rp+R11)
如果 Rx != 0: 打印(“Err (2):”, Rx)
Rx=R11 – (R22*(Rp+R23)/(R22+Rp+R23) / K22)
如果 Rx != 0: 打印(“Err (3):”, Rx)
返回
def par(r1,r2): 返回(r1*r2/(r1+r2))
eo=eo12
R1 = R11
R2 = R1*((eo/Vref) -1)
R22 = R2*Rpot / (Rpot – R2)
eo=eo21 #5.1V
#R1 = R11 + R21*Rpot / (R21 + Rpot)
#R2 = R1*(eo/Vref -1)
#R23 = R2
#eo=eo22 #24V ??
#R1 = R11
#R2 = R23 + R22*Rpot / (R22 + Rpot)
#eo = Vref*(R2/R1 + 1)
#eo22 = eo
#设
K12 = eo12/Vref – 1
K21 = eo21/Vref – 1
K22 = eo22/Vref – 1
Rp = Rpot
Ra = par(Rp,R22)
w3=K22/K21
A=w3*(R22 – K21*Rp) – R22
B=w3*R22*(R22+Rp) – Rp*(w3*K21*(Rp+R22)-R22) – R22*R22
C =Rp*R22*(0-w3*K21*(R22+Rp)-R22)
Q=B*B – 4*A*C
#print(A, B, C, Q)
if Q<0: exit(” 退出:Q<0,尝试 R11、Rpot 或范围的其他值”)
R23_1 = (0-B + sqrt(Q)) /2/A
R23_2 = (0-B – sqrt(Q)) /2/A
print(” R23_1, R23_2=”, R23_1, R23_2)
# 因为 R23 应该 > 0:
如果 R23_1>0: R23=R23_1
elif R23_2>0: R23=R23_2
else: print(“错误: R23_1 和 R23_2 都不是正数”)
# 重新计算 eoij 以进行一致性检查
eo12=Vref*(par(Rp,R22)/R11 +1)
eo21=Vref*(par(R23,R22)/(Rp+R11) +1)
eo22=Vref*(par(R22,R23+Rp)/R11 +1)
# 更新
K12 = eo12/Vref – 1
K21 = eo21/Vref – 1
K22 = eo22/Vref – 1
打印(“图 2c:”,f” eo12={eo12:.2f}”,f” eo21={eo21:.2f}”,f” eo22={eo22:.2f}”)
打印(“图 2c:”,f” Rpot={Rpot:.1f}”,f” R11={R11:.1f}”,f” R22={R22:.1f}”,f” R23={R23:.1f}”)
checkEq(R11, R22, R23)
# 由于我们得到的解决方案可能非常敏感,因为在其附近可能存在奇点(即电阻值的微小偏差会对电压产生很大影响) - 因此得出 2 个结论:
# - 电阻 R11、R22、R23 的公差不得低于 1%;
# - 上述解决方案必须被视为初步解决方案,因此我们将通过以下代码使其更:
R23lim=100*R23
R23=R23/3
当 R23 < R23lim 时:
eo21_x??=Vref*(par(R23,R22)/(Rp+R11) +1)
eo22_x=Vref*(par(R22,R23+Rp)/R11 +1)
如果 eo21_x?? – eo21 > 0.2:中断
如果 abs(eo22 – eo22_x) < 0.1:中断 # 如果 eo22-x – eo22 < 0.1:中断
R23 += 10 # +10 欧姆
否则:退出(“全周期”)
打印(f” eo21={eo21_x??:.2f}”,f” eo22={eo22_x:.2f}”,f” R23={R23:.1f}”)
#-代码结束-
来自调整端的 50 μA(典型值)电流 iA(代表误差项)在 R23 上产生压降。该压降与标称 1.25V 的参考电压 Vref 一起决定了电位器 Rp 发生故障时的输出电压:
eoBreak = iA * R22 + Vref
因此,当降低 R22 的值时,可以在一定程度上降低 eoBreak 的值。


