总谐波失真 (THD) 是线路上谐波的数量与线路基频(例如 60Hz)的比率。THD 考虑了线路上的所有谐波频率。THD 可以与电流谐波或电压谐波相关,以下公式可用于计算线路电压的失真:
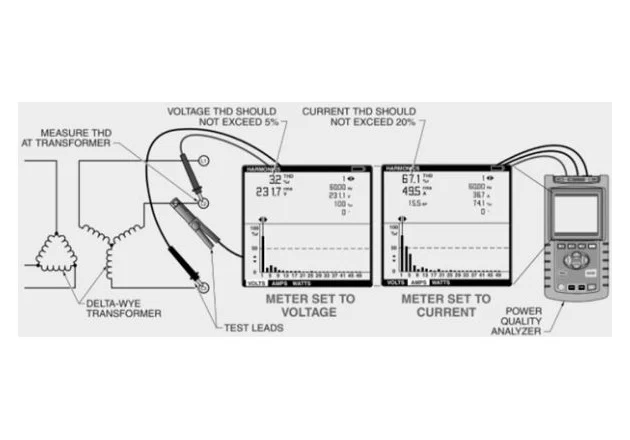
图 1. 应在
变压器处测量总谐波失真 (THD),而不是在负载处测量。
其中 Vn_rms 是第 n 次谐波的 RMS 电压,Vfund_rms 是基频的 RMS 电压。没有高次谐波的纯正弦波形(如理想电压源)的 THD 为 0%。THD 值大于零表示正弦波形已失真。THD 通常以百分比表示,例如 5% 或 50%。可以测量电流和电压的 THD。
电流谐波是由非线性负载引起的,例如那些吸收电流脉冲的负载。电压谐波是由流过不同系统阻抗的谐波电流引起的。流过变压器的电流会导致
线圈两端的电压下降。当电流以脉冲形式流动时,电压也将以脉冲形式流动。高电压失真是一个问题,因为电压失真会成为电机等线性负载的谐波载体。电压谐波会在配电系统和连接到系统的负载中引起问题(额外的热量)。
测量 THD
在对电路进行谐波故障排除时,应测量电压 THD 和电流 THD。为获得结果,电压 THD 不应超过基频的 5%,电流 THD 不应超过基频的 20%。为了准确计算系统中的 THD,应在变压器处而不是在产生谐波的负载处计算 THD(见图 1)。在负载处测量 THD 可提供的 THD 读数,因为整个系统尚未发生 THD 消除。
图 1. 应在变压器处测量总谐波失真 (THD),而不是在负载处测量。
在满载期间测量 THD 电流时,THD 约等于总需求失真 (TDD)。总需求失真 (TDD) 是电流谐波与负载电流之比。在测试或排除系统故障时会进行 THD 测量。TDD 与 THD 不同,因为 TDD 参考的是随时间推移的电流测量值。THD 仅在测量的特定时间对
电源线上的电流进行测量。TDD 测量的目的是考虑 THD 相对较高但总负载相当低的情况。在这种情况下,TDD 相对较低,过热现象被化。
功率因数
功率因数是电路或配电系统中有功功率与视在功率之比。任何交流电路都由有功功率、无功功率、谐波功率和视在功率(总功率)组成。有功功率是电机、灯和其他设备产生有用功所用的功率,单位为 W 或 kW。无功功率是电感器和
电容器存储和释放的功率,单位为 VAR 或 kVAR。无功功率表现为电流和电压波形之间的相移。谐波功率是因谐波失真而损失的功率,单位为 VA 或 kVA。视在功率是 VA 或 kVA,是有功功率、无功功率和谐波功率的矢量和。视在功率不是简单的总和,而是矢量和。
位移功率因数是由于电流和电压之间的相位位移而导致的有功功率与视在功率之比(见图 2)。通常可以在电路或配电系统中添加电容器来校正位移功率因数。位移功率因数的计算方法如下:
PF = cos(θ)
在哪里
PF = 位移功率因数
θ = 电压相位与电流相位之间的差值(相移),以度为单位。
注意:有时使用 DPF 或 PFD 代替 PF 来描述位移功率因数。

图 2. 位移功率因数可用于计算负载实际可用的功率量。
谐波的存在使功率因数的讨论变得复杂。失真功率因数是由于 THD 引起的有功功率与视在功率之比。不能将电容器添加到电路中以补偿失真功率因数。电容器的阻抗随频率而减小。因此,电容器可以成为高频谐波的吸收器。由电容器和电感器组成的特殊类型的变压器或调谐谐波
滤波器可用于校正失真功率因数。失真功率因数的计算方法如下:
$$P{{F}_{THD}}=\sqrt{\frac{1}{1+{{\left( THD \right)}^{2}}}}$$
在哪里
PF THD = 失真功率因数
THD = 总谐波失真
总功率因数是位移功率因数和失真功率因数的乘积,计算如下:
PF总功率= PF × PF总谐波失真
在哪里
PFT ot = 总功率因数
PF = 位移功率因数
PF THD = 失真功率因数
例如,当电压和电流之间的位移为25°,且THD为49%(0.49)时,总功率因数是多少?位移功率因数计算如下:
PF = cos(θ)
PF = 余弦(25°)
PF = 0.906
畸变功率因数计算如下:
$$P{{F}_{THD}}=\sqrt{\frac{1}{1+{{\left( THD \right)}^{2}}}}=\sqrt{\frac{1}{1+{{\left( 0.49 \right)}^{2}}}}=\sqrt{0.8064}=0.898$$
总功率因数计算如下:
PF总功率= PF × PF总谐波失真
PF总计= 0.906 × 0.898
PF总分= 0.814
了解总功率因数很重要,因为它与视在功率有关。视在功率用于确定配电系统元件的大小。
电流波峰因数
电流波峰因数是波形的峰值除以波形的均方根值。电流波峰因数的目的是给出波形中发生多少失真的概念。电流波峰因数的计算方法如下:
$$CCF=\frac{{{I}_{peak}}}{{{I}_{rms}}}$$
在哪里
CCF = 电流波峰因数
I peak = 峰值(单位:A)
I rms = 均方根值(单位:A)
例如,一个完美的正弦波形的电流峰值是多少?在峰值为1的完美正弦波形中,有效值为0.707。
$$CCF=\frac{{{I}_{peak}}}{{{I}_{rms}}}=\frac{1}{0.707}=1.414$$
高电流波峰因数会导致电路和设备过热。为计算机等数字设备供电的 120 V 电路中典型的失真电流波形的电流波峰因数可能约为 2 到 6(见图 3)。一般而言,电流波峰因数较高的电路在高次谐波中所含的能量更多。
电源必须能够以所需的电压和电流提供电路所需的功率。典型的备用电源系统(例如计算机不间断电源)能够在满载时提供 3 的电流峰值因数,但在较低负载时可以表现出更高的峰值因数。
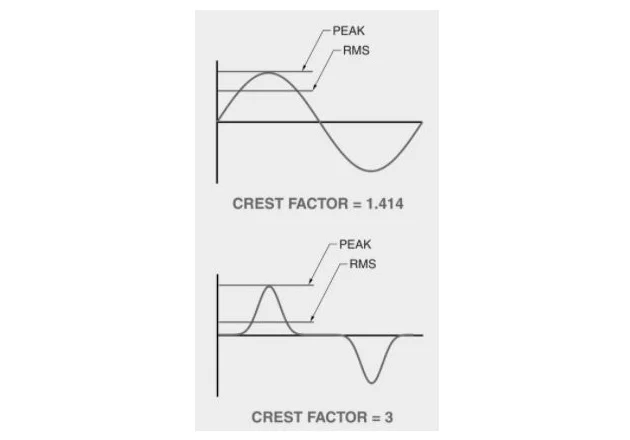
图3. 电流峰值因数比较


