开关模式调节器
开关模式调节器的功能是尽可能高效地将输入电压转换为稳定的恒定输出电压。
此过程会有一些损失,其效率可衡量为
η=POUTPIN?PIN=POUTη→VIN×IIN=(1)VOUT×IOUTη?IIN=VOUT×IOUTη/VIN

图 1. 输入电流与输入电压的关系。图片由 Bodo's Power Systems
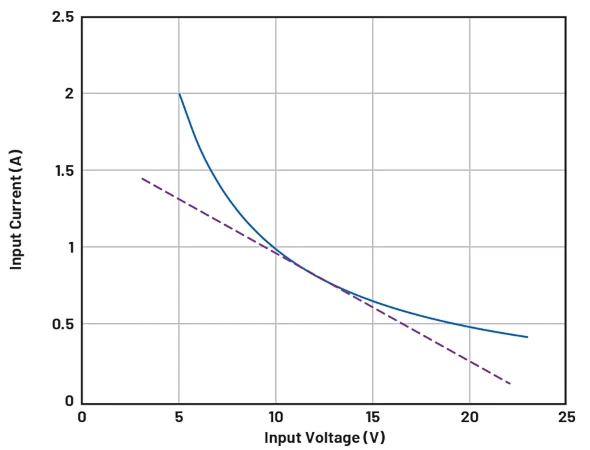
图 2. 添加了 12 V 处的切线。图片由 Bodo's Power Systems
假设调节器保持 V OUT恒定,负载电流 I OUT被视为常数,而不是 V IN的函数。图 1 显示了 I IN与 V IN的关系图。
图 2 显示了工作点 12 V 处的切线。切线的斜率等于工作点处小信号电流随电压的变化。
切线的斜率可以视为转换器的输入电阻 R IN或输入??阻抗 R IN = Z IN (f = 0)。频率 f > 0 时输入阻抗的变化情况将在本文后面讨论。现在,我们假设其在频率 Z IN (f) = Z IN (f = 0) 上为常数。有趣的观察结果是:这个小信号输入电阻为负,因为斜率为负。如果输入电压增加,电流就会减小,反之亦然。
首先,请看图 3 中的电路,其中 SMPS与其输入电容和馈电电感一起形成一个高 Q LC 电路,该电路受负电阻阻尼。如果负电阻在电路中占主导地位,它将成为一个
振荡器,在接近谐振频率时无阻尼振荡。实际上,大信号振荡中的非线性将影响振荡频率及其波形。
此电路中的电感器可能是输入滤波器或电缆的电感。为了使电路稳定,正电阻必须大于负电阻,以使电路衰减。这是有问题的,因为您不希望电感器的串联电阻很高。这会增加散热并降低效率。电容器的串联电阻不应太高,因为电压纹波会增加。
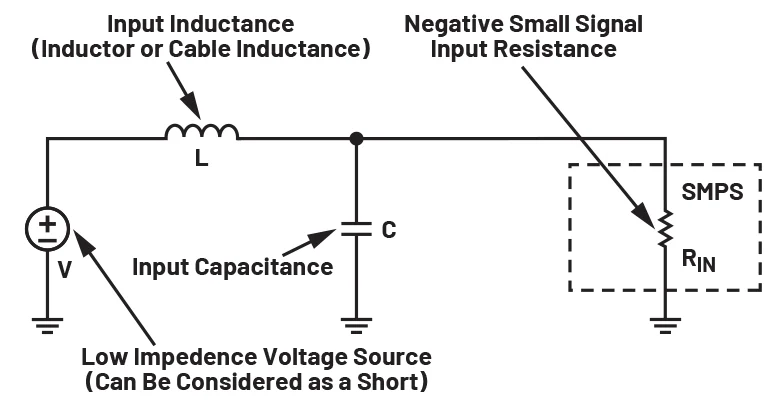
图 3. SMPS 及其输入网络的小信号模型。图片由 Bodo's Power Systems
分析问题
在设计电源系统时,可能会出现以下一些问题:
我的设计是否存在这样的问题?
我该如何分析它?
如果出现问题该如何解决?
如果我们假设输入电路中只有一个有源元件充当负电阻,我们可以通过直接查看 SMPS 的输入来分析阻抗。
如果阻抗的实部在频率上 >0,则电路稳定,假设SMPS控制环路本身稳定。分析可以通过解析或仿真进行。即使输入电路有许多元件,也可以轻松使用仿真,而解析设计则更难。我们将使用 LTspice 开始仿真。
首先通过推导公式计算负阻的一阶近似值:
I=PU→dIdU=?PU2→R=dUdI→RIN?UIN2PIN(2)
如果转换器的输入功率为 30 W,则在 12 V 时,其电阻为 –122/30 Ω = –4.8 Ω。输入滤波器由 LC 滤波器组成。假设输入由低欧姆电源供电,则等效电路可以简化并归结为图 4 中具有理想 0 Ω 电源的示例原理图。

图 4. SMPS 及其输入网络示例。图片由 Bodo's Power Systems

图 5. 添加到网络的电流源刺激 (I1)。图片由 Bodo's Power Systems
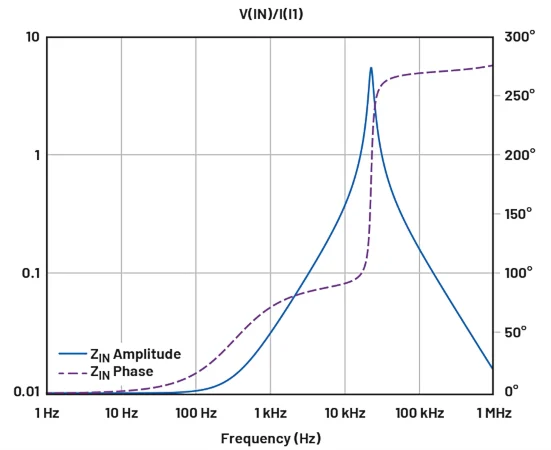
图 6. 注入点阻抗的模拟结果。图片由 Bodo's Power Systems
如果我们在模拟中添加一个电流源,我们可以计算输入端的小信号阻抗为 V(IN)/I(I1)。这在 LTspice 中很容易模拟。
从阻抗图上可以看出,谐振峰位于 23 kHz 左右。在 LC 电路谐振频率附近,阻抗相位进入 90°<相位<270° 的范围,这意味着阻抗的实部为负。我们还可以在笛卡尔坐标系中绘制阻抗,并直接看到实部。值得注意的是,由于 Q 值较高,谐振时的实部变得相当大(-3 Ω)。
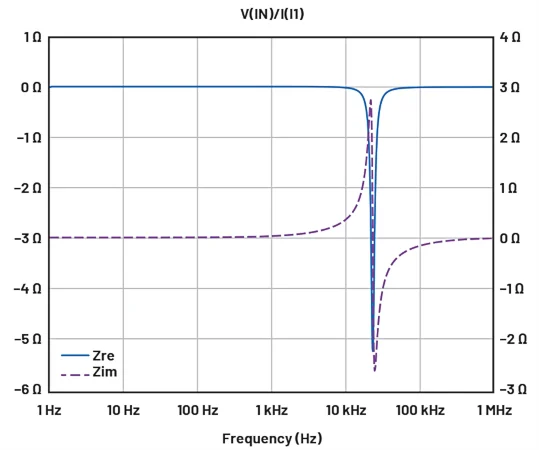
图 7. 与图 6 所示的阻抗相同,但采用笛卡尔坐标。图片由 Bodo's Power Systems
时间域模拟中,注入 1 毫秒的瞬态干扰,导致图 8 所示的不稳定行为。

图 8. 在 1 毫秒时注入瞬态的模拟。图片由 Bodo's Power Systems
如前所述,出于显而易见的原因,我们不想在设计中的电抗部分添加串联电阻。我们可以做的一件事不会对设计产生负面影响(除了其尺寸),那就是添加一个阻尼电容器,该电容器具有相同或更大的电容幅度,其串联电阻适合在感兴趣的频率下控制阻抗。为了获得合理的阻尼结果,该电容器的尺寸应至少比现有的输入电容大一个小倍。串联电阻应明显低于 SMPS 的负电阻,但等于或大于有问题频率下添加电容的电抗。如果添加非陶瓷大容量电容器,其寄生 ESR 本身可能足够好,假设存在元件变化的裕度。
如何选择阻尼电容器及其串联电阻
在 LTspice 中使用反复试验,或者如果电路简单,则使用以下分析方法来检索值。
首先,计算输入电容器和输入电感的谐振频率,如果与输入滤波器相比,电感器另一端的电源可被视为低欧姆,则可认为输入电容器和输入电感并联在 SMPS 输入和交流地之间。
F=12×π×√大号×C吨(3)
在谐振频率处,电容器和电感的电抗的相等。
|X大号|=|XC|=√大号C(4)
由于 X L = –X C且 R L和 R C通常比电抗小得多,因此该公式可以近似和简化。
是磷ArA升升埃升=?X大号×XCR大号+RC(6)
,输入 X = √L/C 和 X = –√L/C 的值。
是磷ArA升升埃升=大号C×1R大号+RC(7)
这是输入滤波器在谐振时的等效并联电阻。
如果该电阻低于SMPS负电阻的,则正电阻占主导地位,输入滤波器网络将会稳定。
如果没有,或者裕度很小,则必须增加阻尼。
这可以通过前面提到的额外电容器来实现,并选择串联电阻以实现阻尼。参见图 9 中的 R1 和 C2。

图 9. 阻尼网络 R1 和 C2 被添加到输入端。图片由 Bodo's Power Systems [PDF]提供
额外电容的值必须等于或大于滤波电容。输入滤波器谐振频率下的电容电抗必须明显低于 SMPS 负电阻的,如果满足个条件,通常就是这种情况。
额外电容的大小是一种折衷。一个设计目标可能是接近输入滤波器的临界阻尼。这可以通过计算产生临界阻尼的并联电阻来实现,当并联电阻为电抗值的一半(Q = 1/2)时,就会发生这种情况。这意味着输入滤波器的并联电阻与负 SMPS 电阻并联,与所讨论的(负)阻尼电阻 R DAMP并联,应等于谐振时输入滤波器 C 和 L 电抗的一半:
R德A米磷=12×11√大号C?1大号C×1R大号+RC?1R我否(8)
如果 L/C × 1/(R L + R C ) 和 |R IN |的值远大于√L/C,则该公式可以简化为:
R德A米磷=12×√大号C(9)
对于阻尼电阻,应选择合理大小的阻尼电容。X DAMP = 1/3 × R DAMP是一个建议值,这意味着如果上述 L/C × 1/(R L + R C ) 和 |R IN | 远大于 √L/C 的假设仍然有效,则 C DAMP = 6 × C。
输入不会达到临界阻尼,但很接近。如果可以容忍更多的振铃并且设计裕度足够稳定,则可以使用较小的 C。在我们的示例中
R德A米磷=12×√4.7μH10μF=0.69Ω(10)C=6×10μF=60μF
使用 0.68 Ω 和 68 μF,如图 10 所示。干扰和交流阻抗的时间域响应如图 11 和 12 所示。
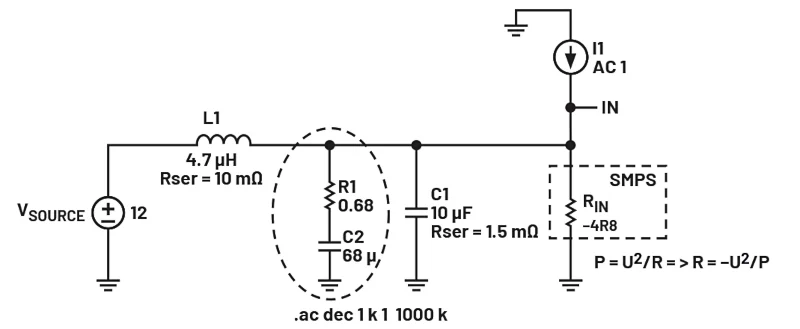
图 10. 阻尼网络及建议元件值。图片由 Bodo's Power Systems

图 11. 时域瞬态响应。图片由 Bodo's Power Systems
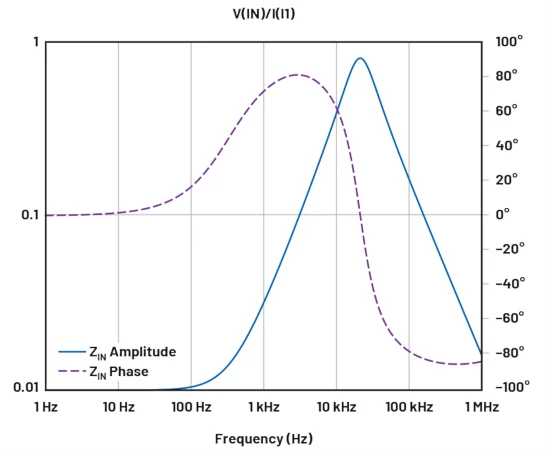
图 12. 阻抗与频率的关系。图片由 Bodo's Power Systems
负电阻的频率行为
您可能认为电源单元 (PSU) 在控制环路带宽之外将不再表现为负电阻——但这通常是错误的假设。如果 PSU 处于电流模式,则对正输入电压变化的即时响应将是占空比变化,以保持稳压器要求的峰值电流值。这意味着如果电压增加,输入电流将瞬间减小,反之亦然。
因此,负电阻一直保持到开关频率。如果 PSU 是电压模式控制的,则通常存在从输入电压到占空比的前馈函数,这将使转换器立即响应输入电压变化以保持输出电压恒定。这也是由于负电阻一直存在到开关频率。问题是,减少控制环路带宽通常不能解决问题。此外,如果下游转换器是稳压的,未稳压的总线转换器仍然看起来像负电阻。











