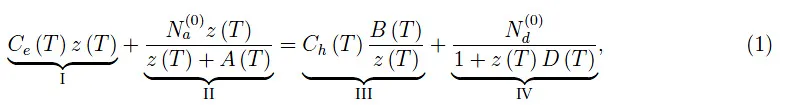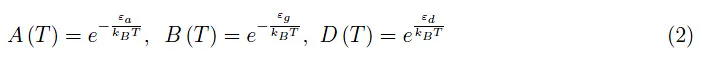在本教程中,我们将研究
半导体中两种杂质(五价和三价)均匀存在的现象,这与 pn 结不同,后者呈现掺杂不
连续性。
主导掺杂
我们在硅样品中掺杂了五价和三价杂质,例如磷和铝
原子。调节逸度 z(T) 随温度变化的方程
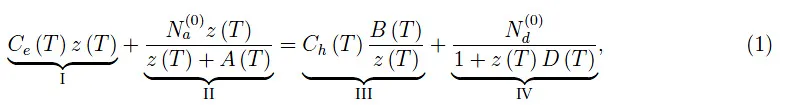
如下:
电力
电子科学笔记:P/N 型半导体
化学势为:μ (T) = kBT ln z (T)。在方程 (1) 中,各个项为:I=导带中的电子数,II=以 ε a 为中心的带隙中能级中的电子数,III =价带中的空穴数,IV=以 ε d为中心的带隙中能级中的电子数。整数 N a (0)、N d (0)分别是五价(受体)和三价(施主)杂质的总数,而函数 Ce,h (T) 已在之前的教程中定义,并且取决于 T 3/2。现在我们可以引入无量纲量:
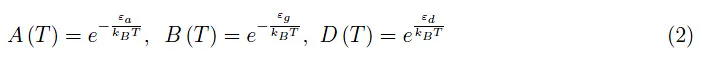
电力电子科学笔记:P/N 型半导体
与上一教程(受体)中研究的情况不同,
研究方程(1)在低温极限下的行为并不具备计算优势,因为其中 I 项可以忽略不计。
事实上,得到的函数方程仍然是三次方程,无法通过分析求解。
尽管方程(1)更复杂,但 Mathematica 软件并没有显示四舍五入
(就像之前分析的模拟1中出现的那样)。例如,对于 N a (0) = 100, N d (0) = 1,我们
得到了图 1 所示的趋势。这种行为除了是 p 型半导体的典型行为外,还符合费米能级ε F
= μ (0)的定义,因为在这种情况下,T = 0 时的化学势的值与该温度下占据的能级的能量相一致(实际上,我们应该考虑以 ε d为中心的能级,但后者的粒子数可以忽略不计,因为 N d (0) N a (0) )。

图1:分别掺杂Na(0)=100、Nd(0)=1受体原子和施主原子的硅样品的化学势趋势
注释 1 – 我们提醒您,在我们的模拟中,各个数量(N a (0) , N d (0) , T)所假设的值都是指示性的。
正如预期的那样,对于 Na(0) ? Nd(0),半导体实际上是 p 型,因为
ε d中的电子数可以忽略不计。在相反的情况下,即 N d (0) ? N a (0),半导体实际上是 n 型,
如图 2 中的图表所示,其中,即使在给定的温度范围内,化学
势也取正值(金属的典型行为)。

图 2:掺杂 Na(0)=1、Nd(0)=100 的硅样品的化学势趋势。当 T → 0 时,化学势稳定在 ?εd 附近。这种行为是 n 型半导体的典型特征。
图 2:掺杂 Na(0)=1、Nd(0)=100 的硅样品的化学势趋势。当 T → 0 时,化学势稳定在 ? ε d附近。这种行为是 n 型半导体的典型特征
,对于 N d (0) = N a (0),我们预期会出现本征半导体的典型行为。

图 3 中的图表证实了这一点。图 4 总结了个别情况。
图 3:掺杂 Na(0)=Nd(0)=100 的硅样品的化学势趋势。当 T → 0 时,化学势稳定在 ?εg/2 附近。这种行为是本征半导体的典型特征。
图 3:掺杂 Na(0)=Nd(0)=100 的硅样品的化学势趋势。当 T → 0 时,化学势稳定在 ? ε g /2 附近。这种行为是本征半导体的典型特征

图 4:三种可能情况下的化学势
电导率
基于上一期开发的算法,通过公式 (1) 计算单位体积硅样品的逸度 z(T),我们可以确定电导率:

电子和空穴的浓度,即量 n(T)、p(T),通过以下方程与逸度相关:

电力电子科学笔记:P/N 型半导体
在方程 (3) 中,我们解释了除电子和空穴迁移率 μe、μh 之外的各种量的温度依赖性。在单位制中,迁移率以 cm2 V1 s1 为单位;对于 Si,μe = 1600 cm 2 V1 s 1,μh = 400 cm 2 V ?1 s ?1。电子电荷的为 e = 1.60217733 × 10 19 C。
在图 5 中,我们以对数刻度了电导率趋势,该趋势是 1/T 的函数,其中
不规则的振荡是由于 Mathematica 四舍五入造成的。拐点对应于
受体完全电离时材料的耗尽。
其余情况以类似方式研究(N d (0) Na ( 0),N d (0) = Na ( 0))。

图 5: Na(0)=100、Nd(0)=1 时σ (1/T) 的对数趋势
结论
刚刚进行的计算分析将使我们能够在后续工作中研究
砷化镓 (GaAs) 作为用于制造电子电路的半绝缘体的行为。