B 类放大器的组成及其特性概述

　　我们将介绍 B 类放大器的组成及其特性概述。然而，我们将在后面的部分中看到，为了正常工作，需要两个互补晶体管以确保输入信号的再现，这就是通常所说的推挽配置。此外，我们将重点介绍 B 类放大器中发生的不良失真以及限制它的一些可能的解决方案。在本教程的一部分，我们将逐步介绍如何计算 B 类放大器的理论效率。
　　B类放大介绍

　　与A类放大器的主要区别在于B类放大器的导通角为180°。这意味着只有一半的输入信号被处理以实现放大过程。为了澄清这一论断，下面的图 1比较了 A 类放大器和 B 类放大器的导通角：

　　图 1：基于 NPN 的 A 类和 B 类放大器导通角

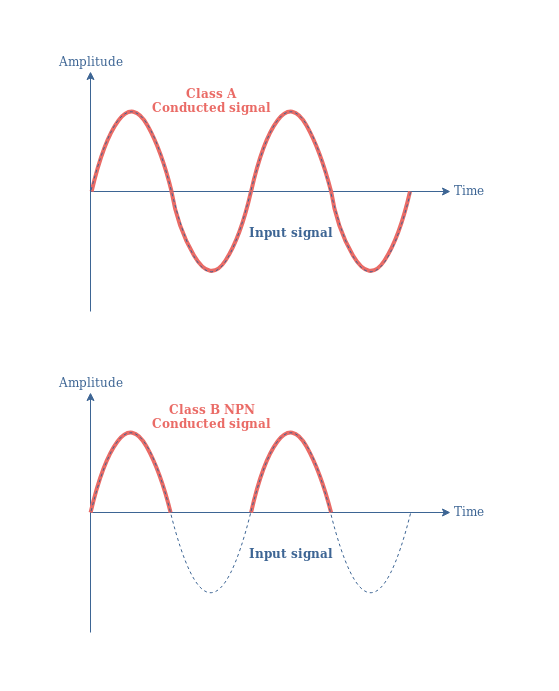
　　在图1中，我们假设使用的双极晶体管（BJT）是NPN型。在 B 类放大器中，PNP BJT 将仅放大信号的负部分，如下图 2所示：

　　图 2：基于 PNP 的 B 类放大器导通角

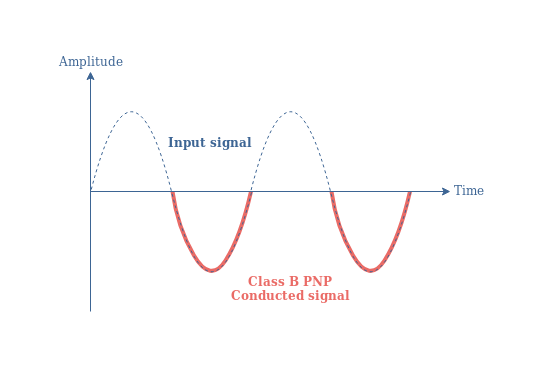
　　为了更好地形象化 B 类配置如何放大信号，让我们考虑信号增益为 5 的两个晶体管，一个 NPN 和一个 PNP。幅度为 1 的输入信号以及 NPN 和 PNP 晶体管的输出信号可以绘制在图 3 的同一张图中：

　　图 3：基于 NPN 和 PNP 的 B 类放大。使用 MatLab 绘制
　　由于NPN晶体管仅放大正半波，而PNP晶体管仅放大负半波，因此仅用一个晶体管无法实现忠实再现。然而，从图 3中，我们看到 NPN 和 PNP 输出的叠加重新生成了输入信号的形状。为了组合这两个输出，NPN 和 PNP 晶体管被放置在所谓的推挽配置中（图 4），我们将在下一节中详细介绍。B 类放大器的另一个重要特性是晶体管基极支路上没有直流偏置。因此，B类放大器仅当交流输入信号高于双极晶体管的阈值电平+0.7V时才能导通。这一事实在触发 B 类放大中常见的不良效应方面发挥着重要作用，我们也将在下一节中澄清这一点。
　　推挽式配置

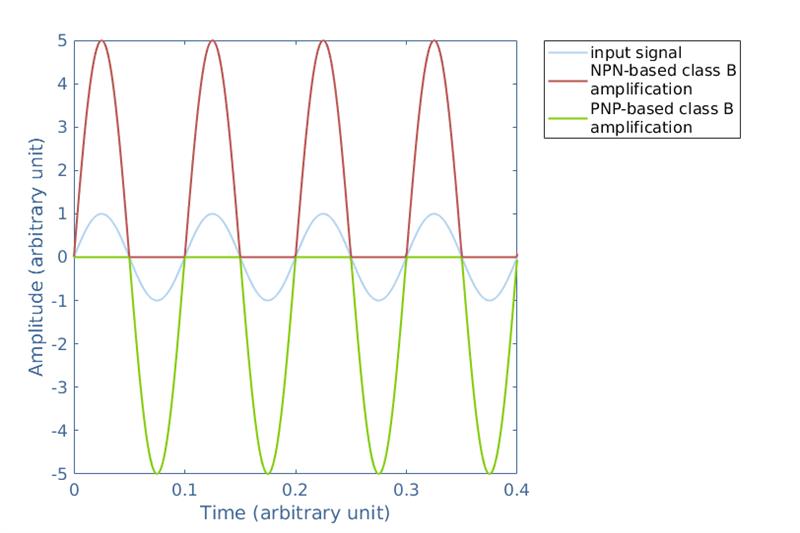
　　下面的图4显示了用于 B 类放大的射极跟随器推挽配置的输出级，以及输入信号、NPN 和 PNP 晶体管的输出以及终组合输出：

　　图 4：B 类推挽配置

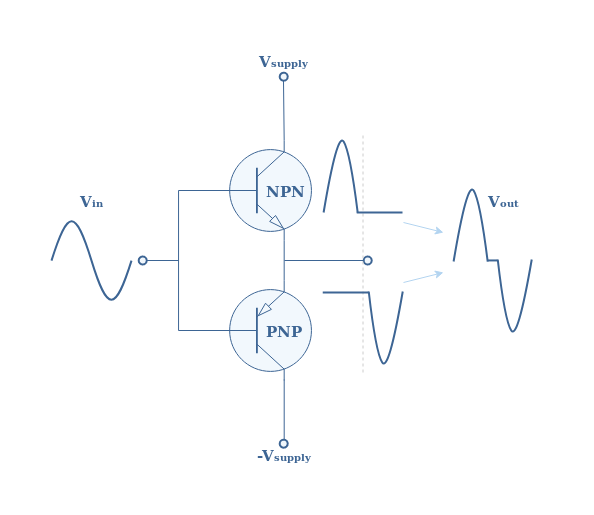
　　图 4突出显示了通常称为交叉失真的不良效应。零幅度交叉周围确实存在一个信号未忠实再现的区间。为了理解为什么这种现象专门发生在 B 类放大器中，我们需要绘制推挽配置的(V out , V in ) 特性：

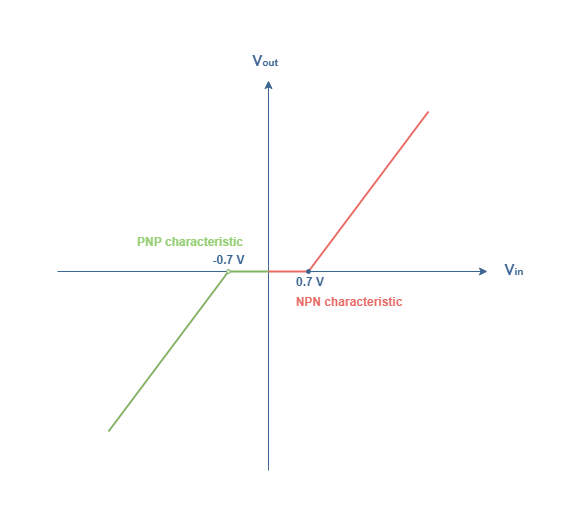
从图 5中，我们可以看到 B 类推挽配置的输出/输入特性仅是部分线性的。事实上，在 B 类放大器中，NPN 和 PNP 晶体管工作在截止区域，当输入信号低于 +0.7 V 阈值（或高于 -0.7 V）时，NPN 晶体管（或 PNP）不会工作。传导信号。此行为会在 -0.7 V 和 +0.7 V 之间创建 1.4 V 的间隔，其中基极和发射极分支之间无法传导信号。这解释了 B 类推挽配置中观察到的交叉失真。

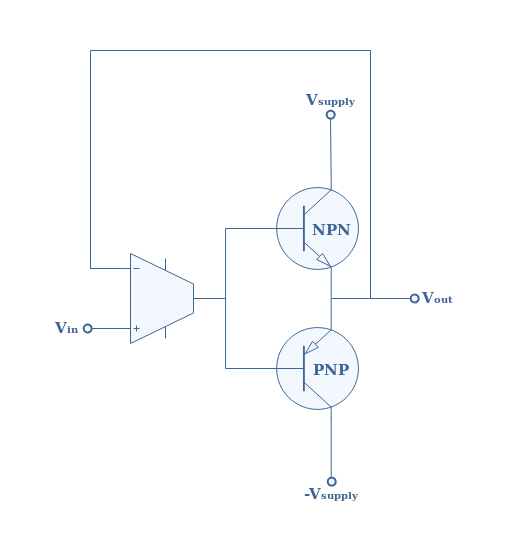
　　限制交叉失真

　　交叉失真需要进行校正，特别是对于音频放大器来说，这种效应是显而易见的。限制或完全消除失真的个可能的解决方案是根据输出信号的所需线性度或多或少地偏置基分支。该解决方案将在下一个教程中详细介绍，因为稍微偏置基极分支对应于 AB 类放大。另一种解决方案是修改图 4，在从输出到输入的电路中添加一个运算放大器，如下图 6所示：

　　图 6：负反馈推挽配置
　　首先，请务必记住，运算放大器比较反相支路 (-)和非反相支路 (+)上的两个输入。运算放大器具有非常重要的增益，因此微小的差异可以被高度放大。仅当两个输入信号严格相同时，运算放大器（在我们的例子中为公共基极分支）的输出才等于零。让我们考虑一下，在 B 类负反馈推挽配置的输出处可以观察到或多或少重要的交叉失真。当忠实地再现在[-0.7V，+0.7V]区间之外的输出信号时，支路+、V +处的电势严格等于支路-、V-处的电势。因此，电位差V + -V-为零，运算放大器没有放大任何信号。因此双极晶体管的公共基极支路没有被偏置。如果输出信号处于交越失真区间[-0.7 V，+0.7 V]，则运算放大器端子处将出现电位差V + -V – 并被放大到共基极支路，从而对晶体管进行临时偏置以纠正失真。总而言之，我们可以说该电路“强制”输出保持与输入相同的形状，从而再现忠实的信号。
　　B级效率

　　如前面的教程所述，放大器的效率由比率η=P out /P abs定义，其中 P out是输出功率，P abs是晶体管和负载吸收的功率，以实现放大过程。在下一节中，我们可以参考图 4，记住输出信号是在负载电阻 R L上获取的。正如之前有关A 类放大器的教程中所见，我们可以分解输出信号 V out (t) 和 I out (t)，例如：其中(V 0 ,I 0 )代表偏置，(v out (t),i out (t))代表交流分量。替代信号也可以重写，例如：在交流状态下，负载中的耗散功率 P RL由以下比率表示：

　　eq 1：负载功耗

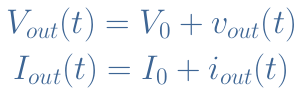
　　两个晶体管消耗的瞬时功率p(t)可根据公式 2写出：

　　eq 2：晶体管中的瞬时耗散功率

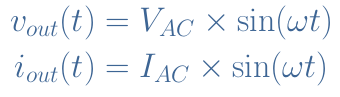
　　我们可以通过积分运算（这里不再详述）证明晶体管中消耗的平均功率P A满足公式 3：

　　eq 3：晶体管的平均耗散功率

　　因此，电源提供的总功率P abs只是负载和晶体管 P RL +P A中消耗的功率之和 ：

　　eq 4 : 实现放大过程吸收的功率

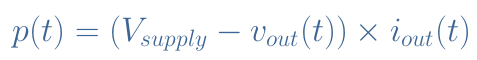
　　，效率可以用比率 η=P RL /P abs来表示：

　　eq 5：推挽式 B 类配置的效率

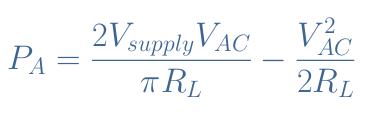
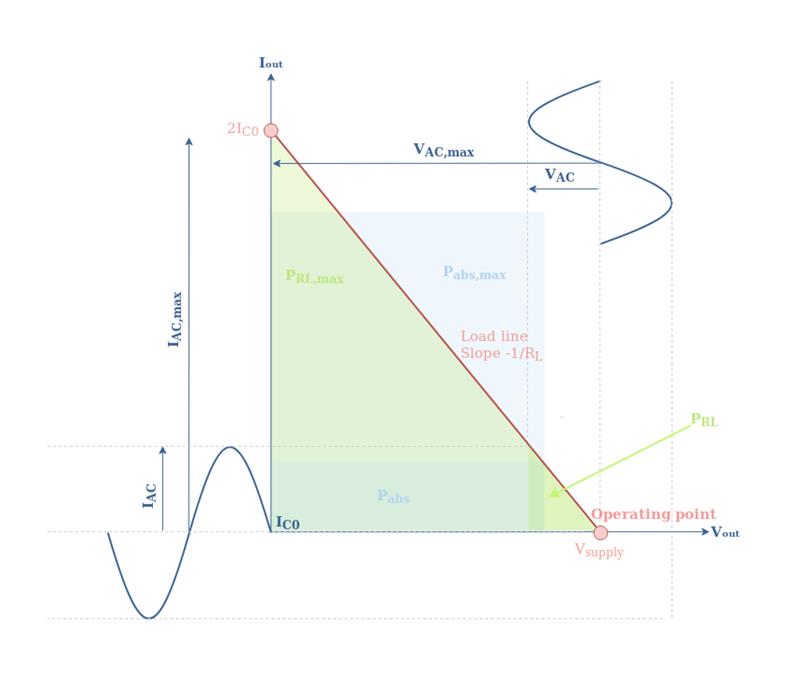
　　当V AC =V Supply时效率化，因此给出理论效率η max =π/4=78.5 %。与 A 类放大相比，这是效率的重要改进，A 类放大使用变压器只能实现理论上的 50%，而这会导致额外的成本和复杂性。上述信息可以总结为显示功率分布的图表，如图7所示。重要的是要记住绘制此图 V AC /R L =I AC。此外，为了表示数量 Pabs ，我们将其重写为 Pabs = (V Supply ×√2/pi)×(I AC ×√2/pi)((V Supply ×0.8)×(I AC ×0.8 ）。

　　图 7：B 类放大器的功率分布
　　结论
　　本教程通过介绍此类配置的特性来重点介绍 B 类放大器。事实上，我们已经看到 B 类放大的行为与 A 类相反：它仅呈现180° 的导通角，并且不能忠实地再现信号。后来，研究表明可以组合两个 NPN 和 PNP 晶体管，以实现更忠实地再现输出信号的推挽配置。NPN 晶体管负责放大正半波，PNP 晶体管对负半波执行类似的过程。然而，这种配置会产生交叉失真，导致零信号区附近的正半波和负半波未对准。正如在同一部分中详细介绍的，这种现象来自于施加到推挽配置的公共基极分支的零偏压，以及 NPN 和 PNP 晶体管的阈值电压，仅允许信号输出导通。 [-0.7 V,+0.7 V] 零信号间隔。之后，我们重点关注可能实施的解决方案，以解决交叉失真问题。其中之一是根据我们想要实现的所需线性度来偏置基分支。该解决方案将在下一个有关AB 类放大器的教程中详细介绍。第二种解决方案是添加运算放大器以在电路中创建负反馈环路。运算放大器迫使输出信号遵循输入信号的形状，从而限制或消除不需要的交越失真。