传输线
变压器的宽带功能使其在射频应用中非常有用。这些变压器有多种配置,具体取决于所使用的传输线的类型、数量和布置。本系列之前的文章探讨了guanella 1:1和guanella 1:4巴伦,这两个经典电路由Gustavguanella 于1944 年首次提出。
在本文中,我们将通过进行简化分析,对 Ruthroff 变压器(包括平衡到不平衡和不平衡到不平衡)有基本的了解。
Ruthroff 1:4 不平衡至不平衡变压器
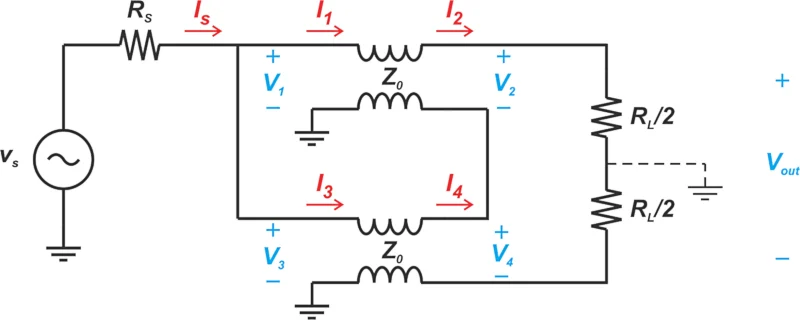
图 1 显示了我们已经熟悉的配置——Guanella 1:4 巴伦,它包含两条传输线。
瓜内拉 1:4 巴伦。
图 1.Guanella 1:4 巴伦。
当不需要巴伦功能时,我们可以重新排列单个双线
线圈以提供1:4的阻抗变换比。图 2 描绘了该电路,称为 Ruthroff 1:4 不平衡至不平衡变压器。您可能还会看到它被称为 Ruthroff 1:4“unun”,与我们将“平衡至不平衡变压器”缩写为“巴伦”相呼应。我和许多其他人一样,发现“unun”这个词不优雅且没有吸引力,因此选择不使用它。
Ruthroff 1:4 不平衡至不平衡变压器。
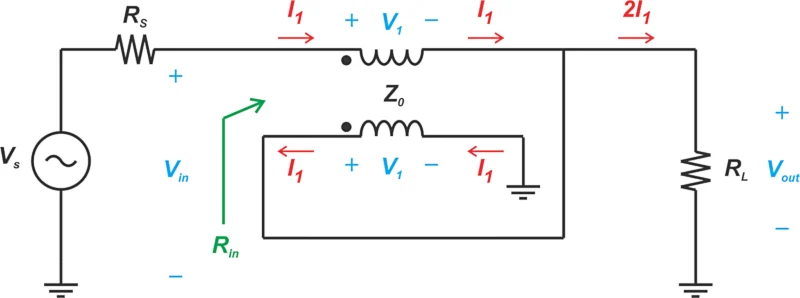
图 2.Ruthroff 1:4 不平衡至不平衡变压器。
我们使用上一篇文章中介绍的集总
电感方法来分析该电路。
假设通过上绕组的电流为I 1,其两端的电压降为V 1。由于变压器的作用,V 1的电压差也施加在下部绕组上,并且I 1的电流以指示的方向流过该绕组。因此,通过负载的电流等于 2 I 1。
由于下部绕组与负载并联,因此负载两端的电压 ( V out ) 也等于V 1。输入端的电压可以通过将上部绕组和负载电阻上的电压相加来轻松确定,从而得出:
V输入 = V1 + V输出 =2V1
等式 1。
对于负载电阻 ( R L ),欧姆定律定义了V 1和I 1之间的另一种关系:
RL = Vout2I1 = V12I1
等式2。
现在,我们用V 1和I 1来表示输入电阻 ( R in ) ,并使用公式 2 进行简化:
Rin = VinI1 = 2V1I1 = 4RL
等式 3。
等效输入电阻是负载电阻的四倍。为了更快地分析上述电路,请记住以下几点:
输入电压等于两个绕组上的电压降之和 ( V in = V 1 + V 2 )。
由于变压器的作用,两个电压降相等 ( V 1 = V 2 )。
输出电压等于其中一个绕组的压降 ( V out = V 1 = V 2 )。
因此,输入电压是输出电压的两倍(V in = V out + V out = 2 V out)。
将电压改变两倍的无损网络会产生 1:4 的阻抗变换比。
与guanella 配置一样,Ruthroff 变压器不提供直流隔离。理想情况下,这两种变压器类型在奇模激励期间在磁芯材料中感应出的净磁通为零。这显着降低了磁芯的频率相关磁滞损耗,这通常决定了变压器带宽的上限。
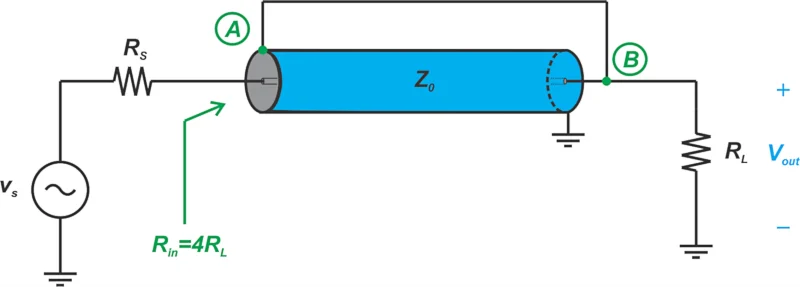
图 3 展示了 Ruthroff 电路的同轴实现。请注意,同轴线通常会装载铁氧体
磁珠,尽管图中未显示这些铁氧体磁珠。
Ruthroff 1:4 不平衡至不平衡变压器的同轴实施。
图 3.Ruthroff 1:4 不平衡至不平衡变压器的同轴实现。
为了使漏感, A点和B点之间的距离应尽可能短。这可能需要弯曲线以使连接点靠近在一起。另请注意,在 Ruthroff 变压器中,线路 ( Z 0 ) 的特性阻抗等于输入和输出阻抗的几何平均值: Z0 = √RSRL
等式 4。
Ruthroff 1:4 巴伦变压器
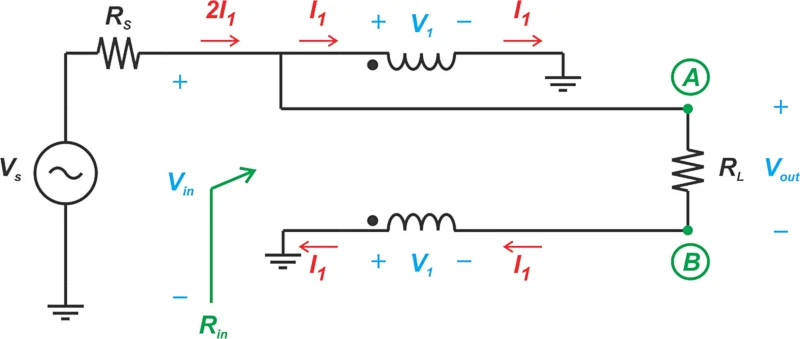
图 4 显示了 Ruthroff 1:4 巴伦。与不平衡到不平衡变压器一样,它是围绕单个双线线圈构建的。
Ruthroff 1:4 巴伦。
图 4.Ruthroff 1:4 巴伦。
由于变压器的作用,两个绕组上再次出现相同的电压。通过将绕组的适当
端子接地,在负载电阻端子处产生相反极性的电压。换句话说,节点A和B具有相同的电压,但极性相反。
从电路图中很容易看出,输入电压等于一个绕组上的压降(V in = V 1),而负载上的电压为V out = 2 V 1。因此,该电路将输入电压加倍,产生 1:4 的阻抗变换比。由于负载两端都不接地,因此输出是平衡信号。



