如何分析传输线变压器：简单的方法和困难的方法

　　通过使用传输线代替绕组，传输线变压器能够在高频和宽带宽下运行。正如我们在之前的文章中了解到的，这些功能使其在射频和微波应用中非常有用。然而，初学者经常发现传输线变压器难以分析。

　　在本文中，我们将尝试通过介绍传输线变压器分析的两种常用方法来消除一些混乱。我们将研究的种方法（本文标题中的“困难方法”）提供了更高的准确性，但代价是花费更多的时间进行数学计算。第二种方法提供了一种简化的分析，通常但并非总是足够。在采取简单的方法之前，了解困难的方法很重要。

　　困难的方法：使用传输线方程

　　传输线变压器依靠电磁波通过传输线传播来将能量传输到输出。因此，严格的分析应考虑传输线方程。例如，图 1 显示了采用双线线圈构建的反相器电路。

　　使用双线线圈构建的宽带相位逆变器图。

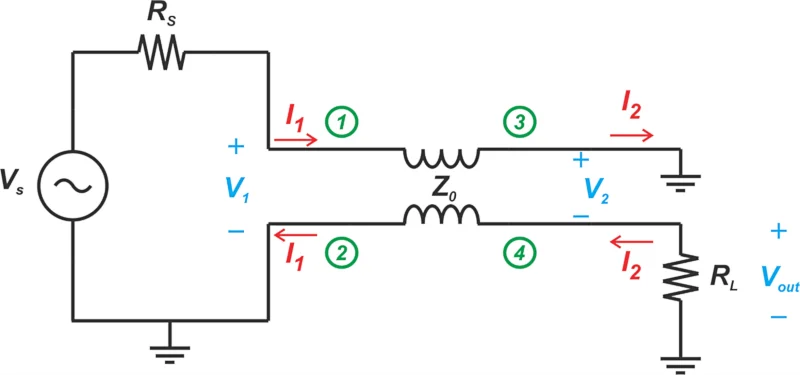
　　图 1.采用双线线圈构建的宽带相位逆变器。

　　为了分析该电路，我们将使用传输线的 ABCD 参数来描述传输线的输入和输出端口之间的关系。考虑图 2 中的无损传输线，其特征阻抗为Z 0，相位常数为 β ，长度为l。

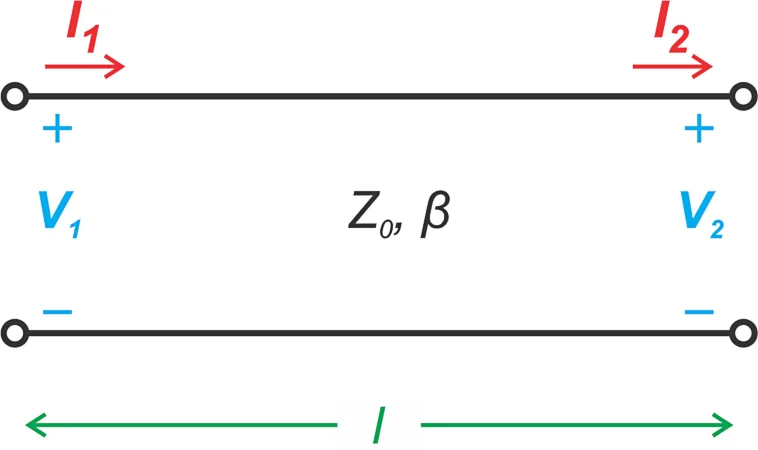
　　无损传输线。

　　图 2.具有特性阻抗Z 0 、相位常数β和长度l的传输线。

　　传输线的 ABCD 表示通过以下方程描述输入和输出端口的电压和电流量：

　V1 = cos(βl)V2 + jZ0sin(βl)I2

　　等式 1。

　　I1 = jsin(βl)Z0V2 + cos(βl)I2

　　等式2。

　　这是我们用来分析反相器电路的两个主要方程。我们还将从图 1 中获得一个附加方程来关联输出电压和电流：

　V2 = RLI2

　　等式 3。

　　其中RL是负载电阻。

　　假设负载匹配( Z 0 = R L )，我们可以使用一些代数将公式 3 与公式 1 结合起来。这给出了输入和输出电压之间的关系：

　V2 = e?jβlV1

　　等式 4。

　　正如该方程所示，对于匹配的负载，沿传输线的信号幅度是恒定的。该线路仅向输入信号引入相移。

　　终输出电压计算如下：

　Vout = ?V2 = ?e?jβlV1

　　等式 5。

　　这表明，如果指数项的相移可以忽略不计，则电路充当反相器。为了使传递函数表现出 180 度相移，我们应该有

　　回想一下，相位常数 β 由下式给出：

　   β = 2πλ

　　等式 6。

　　因此，为了忽略指数项的相移，线路的长度应满足以下约束：

    　l ? λ2π

　　方程 7.

　　总而言之，电路要充当反相器，必须满足两个条件：

　　线路损耗必须可以忽略不计。

　　线路的长度必须足够短，以便忽略指数项的相移。

　　这种方法虽然准确，但数学量相对较大。我们来讨论一种更直观的方法来确定电路的阻抗变换比。

　　简单的方法：集总电感器方法

　　在分析阻抗变换时，许多书籍都假设传输线变压器的行为与磁耦合变压器类似。这个假设使我们能够避免上一节中看到的复杂数学。例如，让我们看看如果我们分析反相器电路（为了便于参考而在图 3 中重现）将其视为磁耦合变压器，会发生什么情况。

　　采用双线线圈构建的宽带相位逆变器，但作为磁耦合变压器进行分析。

　　图 3.将宽带反相器作为传统变压器进行分析。

　　在这种情况下，我们假设初级绕组上的电压 ( V 1 ) 也施加在次级绕组上 ( V 1 = V 2 )。同样，相同的电流流过初级和次级绕组。为了找到电压的极性和电流的方向，我们将变压器点约定应用于上图。应用基尔霍夫电压定律，我们得到：

　Vout = ? V 2 ? V i n + V 1 = ? V i n        

　　方程 8.

　　这与我们之前进行的更的数学分析是一致的。

　　如果应用正确，简化的方法将提供与更严格的分析相同的阻抗变换比。因此，许多参考文献仅提供简化的分析。然而，这种方法依赖于我们对电路行为做出某些假设，特别是离开绕组的电流与进入绕组的电流相同。

　　这是我们对集总电感器使用的分析类型。为了假设传输线变压器的绕组充当集总电感器，以下两个陈述必须正确：

　　该电路工作在低频。

　　传输线相对于波长来说很短。

　　由于传输线变压器可以在其相当一部分频率范围内充当磁耦合变压器，因此只要满足上述两个条件，简化的分析就是有效的。然而，在高频下，我们应该使用传输线方程来全面了解电路的行为。传输线分析假设绕组充当分布式元件，从而导致假设进入绕组的电流与离开另一端的电流不同。