这些设计思想涉及微处理器生成的脉宽调制器驱动低通滤波器以生成 DAC。已经推出了解决纹波衰减、稳定时间化和精度限制的方法。这是提议改进基于 PWM 的 DAC 整体性能的一系列 DI 中的第四个。该系列的每项建议都可以独立于其他建议实施。该 DI 解决了 PWM 序列修改问题,从而缓解了低通模拟滤波要求。
PWM 时钟频率F clk Hz 和PWM 分辨率的位数b的组合决定了标准PWM 的频率(F clk ·2 -b Hz) 输出分量。在所有可能的占空比中,该组件也是的,因此对于模拟滤波器抑制来说挑战性。对于给定的 F clk,分辨率位数越多,提供足够抑制的滤波器的稳定时间就越长。但有一种方法可以绕过这个限制。
假设输出为 0 或 1 的标准 8 位 PWM 配置为(任意)121/256 的占空比。256 个状态循环中的前 121 个状态为 1,其余 135 个状态为 0。但是,如果前 128 个状态以 60 个开头,而后 128 个状态以 61 个开头呢?我们将其称为“一分为二”PWM。这两个序列的幅度略有偏移,因此可以在图 1所示的图表上清楚地看到它们。
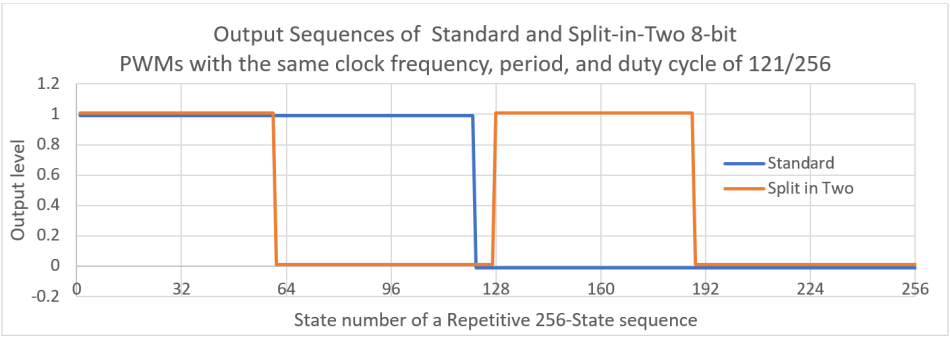
图 1具有相同时钟频率、周期和占空比 (121/256) 的标准和拆分两个 8 位 PWM 的输出序列。
蓝色波形代表标准 PWM,橙色波形代表一分为二的 PWM。为什么后者可能更有优势?考虑图 2中所示的两个 PWM 的频谱。

图 2具有相同时钟频率、周期和占空比 (121/256) 的标准和拆分两个 8 位 PWM 的频率内容。
与标准 PWM 相比,一分为二 PWM 的谐波能量可以忽略不计。谐波所需的衰减已显着减少,所需的衰减现在应用于两倍频率的谐波。现在可以采用随频率衰减较小的模拟滤波器,从而缩短响应占空比变化的稳定时间。
另一种看待此问题的方法是将一分为二的 PWM 周期加倍至 512 个状态,以产生 9 位 PWM。如图 3所示,两个 PWM 的频谱几乎相同,因为时域波形几乎相同 - 它们的不同之处仅在于每隔一个 256 位序列,一个额外的一状态替换一个零状态。更高分辨率的 9 位 PWM 以 8 位基波频率的一半产生少量能量(小于 1%)。任何能够充分抑制 8 位基频的模拟低通滤波器都会充分衰减该频率一半的信号。
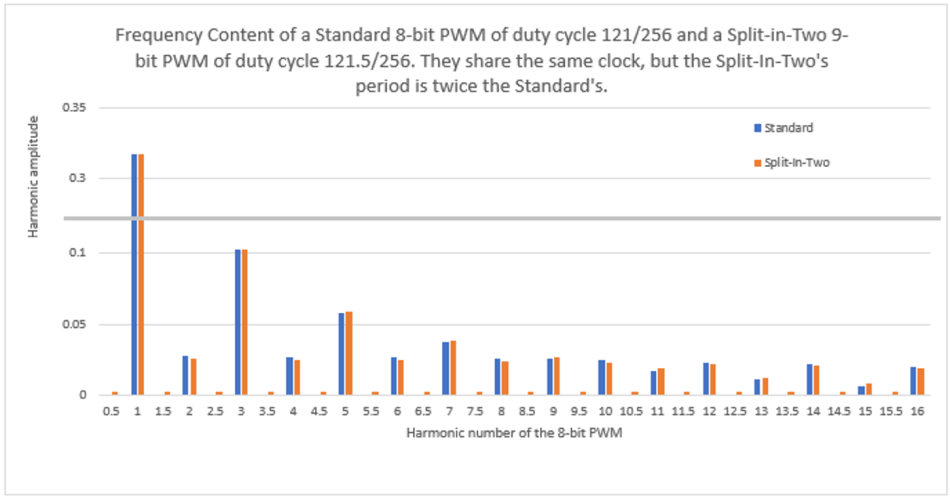
图 3占空比为 121/256 的标准 8 位 PWM 和占空比 (121.5/256) 一分为二的 9 位 PWM 的频率内容。它们共享相同的时钟,但一分为二的周期是标准 PWM 周期的两倍。
超级循环
我们可以将一分为二视为生成一个由 2 b 个状态的两个循环组成的“超级循环”,每个循环至少有 S 个单状态,其中 0 ≤ S < 2 b。在一个周期中,如果超级周期中“1”的总数为奇数,则可以将一个“零”状态交换为“一”状态。这是一个 (b+1) 位 PWM,周期为 2 个b+1状态。但没有理由在两点停下来。可以存在 2 n个循环的超级循环,其中 n 是任意整数。由于每个周期都能够选择性地将一个零状态交换为一个状态,这导致了分辨率为 2 b+n位的 PWM 超级周期。但与标准非超周期 PWM 不同,其频谱能量分量位于 f clk /2 b+nHz,超级周期的 f clk /2 b Hz更高。与一分为二的具体情况一样,这减轻了模拟滤波要求并缩短了稳定时间。
值得将超级循环视为由两个不同序列的总和组成。一种是 S 序列,其中每个周期都由 S 个连续的一状态的相同序列组成。另一种是 X 序列,其中每个周期可选择将一个状态之后的个零状态与另一个单状态交换。X 序列具有 X 个一态,其中 0 ≤ X < 2 n。超级循环的占空比为(2 n ·S + X)/2 b+n。
当一个超级循环的 n = 1 时,只有一个循环可以驻留额外的一状态。但是当 n > 1 时,X 也大于 1,问题就变成了如何将 X 的值分配给 2 n个循环,以限度地减少低频超级循环的能量。Microchip 制造 SAM D21 微控制器的人员不仅为我们解决了这个问题,而且还在硬件中实现了它 [1]!对于该IC,只需将X和S的值写入单独的寄存器即可实现超周期PWM;硬件在无人监督的情况下完成其余的工作。幸运的是,几乎所有微处理器都可以简单地增强标准 PWM 来实现超级循环。对于每个 PWM 周期,必须修改占空比计数,以便在 S 1 序列之后,当且仅当以下 C 表达式对于该周期为真时,个 0 立即更改为 1:
MASK & (cycleNbr * X) > MASK – X
这里,MASK = 2 n – 1,X同前,cycleNbr是超级循环中循环的数字位置。图 4是 n = 4、b = 8 超级周期 PWM 的 32 个谐波的幅度图。该图提供了这种方法的好处的证据。
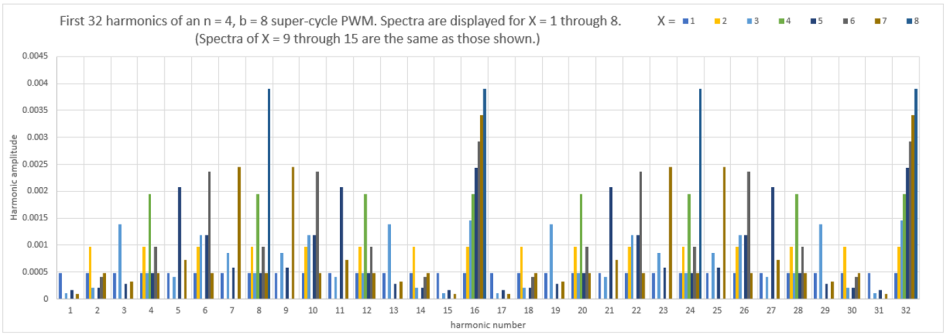
图 4 n=4、b=8 超级周期 PWM 的前 32 个谐波。显示 X=1 至 8 的光谱。(X=9 至 15 的光谱与所示相同。)X序列的能量相对较低,只有0到2 n -1 个单态,但它也呈现出频率分量,fclk/2 n+b Hz。S 序列通常包含迄今为止多的能量(占空比非常小的情况除外),但其频率分量在 F clk /2 b Hz 处明显更高。在 X 序列中,X = 1 给出其谐波的幅度:fclk/2 n+b Hz 处的 2 -11。S 序列的频谱从 X 序列的谐波数 2 4 = 16 开始,并在 S = 2 11时产生该谐波的幅值 2/π。如果这是一个标准 PWM(n = 0 超级周期 — 根本没有超级周期,即只是一个普通 PWM),那么 2/π 的幅度将出现在低 16 倍的频率处。标准 PWM 带来了更为严重的滤波问题。由于需要大量的低频衰减,其滤波器需要更长的时间才能响应占空比变化。
比较 (n+b) 位标准和超周期 PWM 的滤波器
标准和超级周期(及其 X 和 S 序列) PWM 的滤波 AC 稳态时域贡献应小于 PWM 单态电压的某个分数 α。α 的合理值为 2 -(n+b+1) , ? LSB。这意味着 X 序列的谐波处的衰减系数为 1/4。幸运的是,即使是满足此要求的简单两组件 RC 滤波器也能充分衰减所有较高的 X 序列谐波,因此无需满足抑制它们的额外约束。第 16个X 谐波频率是个 S 谐波的频率。其PWM能量需要的衰减系数为(π/2)·2 -(n+b+1)在 50% 占空比下。同样,任何满足此要求的低通滤波器都将充分衰减剩余的 S 序列谐波。对于 F clk = 20 MHz,图 5和图 6是三阶滤波器(两个运算放大器、3 个电阻器和 3 个电容器)的频域和时域阶跃响应图,满足标准 12位和超级周期 n = 4,b = 8(12 位)PWM。
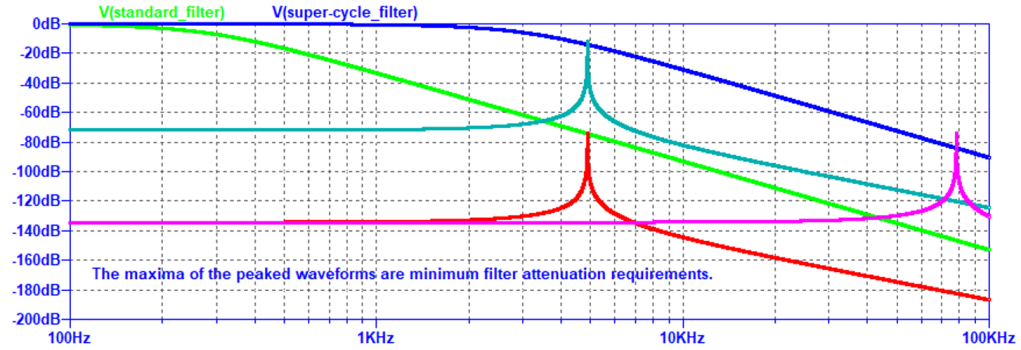
图 5具有 12 位分辨率的标准和超级周期 n = 4 位 PWM 的滤波器频率响应。峰值波形的值是滤波器在峰值频率处允许的响应。滤波器确保其输出处的稳态时域能量小于满量程的 1/2 LSB。
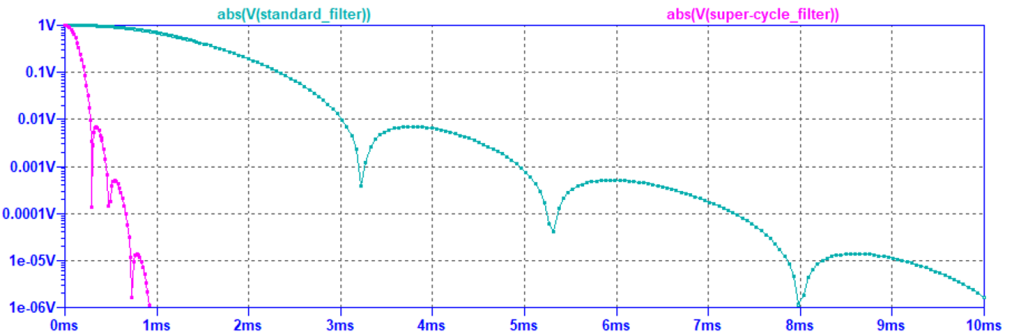
图 6具有 12 位分辨率的标准和超级周期 n = 4 位 PWM 的滤波器时间响应的对数。超级周期 PWM 的稳定时间要短得多,这是显而易见的。
放宽低通模拟滤波器要求
当与适当的模拟滤波器配合使用时,现有微处理器 [1] 中的硬件中可用的 PWM 实施例方法可提供比标准 PWM 显着更短的稳定时间。这种方法可以借助几乎所有微控制器中的少量软件来实现。





