找到错误术语是成功的关键
正如我们在本系列文章前面讨论的,SOLT 校准方法依赖于 12 项误差模型。该模型考虑了由有限方向性、反射跟踪、端口匹配误差等引起的误差。图 1 显示了其正向和反向子模型。
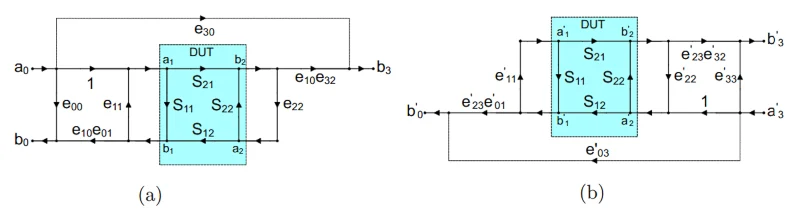
12 项误差模型分为两个组成子模型。
图 1. 12 项误差模型由 6 项正向子模型 (a) 和 6 项反向子模型 (b) 组成。图片由
Mini-Circuits提供
为了从原始测量值中获得 DUT 的真实 S 参数,我们需要纠正上面建模的所有误差。校正过程包括找到 12 个误差项的值并将其应用到数学公式中。尽管这些误差校正的数学计算相对简单,但确定误差项需要准确的标准和测量,这使其成为一项具有挑战性的任务。
某些应用程序可能会给查找错误项带来额外的挑战。例如,确定 DUT 在低温、极端功率水平或使用不寻常连接器时的误差项可能极其困难。不过,一旦误差项已知,需要求解的方程就相对简单。
为了更好地了解校准过程及其要求,让我们更仔细地研究 SOLT 校准。
SOLT 校准过程
SOLT 校准使用短路、开路、负载和直通标准来确定测量系统的误差项。负载、开路和短路标准通常收集到校准套件中;有些套件(例如图 2 中的套件)还包含通过标准。
让我们回顾一下图 1 中的 12 项误差模型。为了找到图 1 中前向子模型的误差项,我们使用以下三个步骤:
应用单端口校准。
确定隔离。
进行直通测量。
虽然我们只介绍前向测量的过程,但可以应用相同的三步过程来查找反向子模型的误差项。我们所要做的就是改变我们插入方程的误差项。
第 1 步:应用单端口校准
在此步骤中,针对三种不同的标准测量正向子模型的输入反射系数 (Г IN ):短路、开路和负载。VNA 测量的输入反射系数与标准的实际反射系数 (Г L ) 之间的关系如下: ΓIN = e00 + e10e01ΓL1 ? e11ΓL
通过测量 Γ L的三个不同值,我们得到三个独立方程,每个方程包含三个未知误差项e 00、e 10 e 01和e 11。在理想情况下,短路、开路和负载标准应分别产生 –1、1 和 0 的Γ L值。当然,我们并不生活在理想的世界中。我们将很快讨论现实世界的短路和开路的反射系数是什么样的。
步骤 2 和 3:确定隔离度和直通测量
为了找到泄漏项 ( e 30 ),我们将匹配负载连接到 VNA 的端口 1 和 2,并测量S 21参数。这是一个可选步骤,现代 VNA 端口之间的泄漏通常可以忽略不计,因此我们可以将泄漏项设置为零,而不会造成重大后果。
,我们使用直通标准将 VNA 的端口 1 和 2 连接在一起。通过测量S 11和S 21参数,我们获得两个独立方程来确定剩余的两个误差项(e 22和e 10 e 32)。
总结一下:
每个端口处的单端口标准(短路、开路和负载)的三次测量总共产生六个独立方程。
完全表征的通过标准总共提供了四个方程——每个测量方向两个。
这两个隔离项是通过将匹配负载连接到端口 1 和 2 来找到的。这为我们提供了另外两个方程。
整个校准过程总共产生 6 + 4 + 2 = 12 个独立方程来求解模型中的 12 个误差项。然而,我们不太可能需要自己解决这些问题——大多数 VNA 都有支持 SOLT 校准的内置软件。我们只需连接适当的标准并让 VNA 执行校准即可。
通常,我们可以假设负载标准是完美的 50 Ω 阻抗。通常还给出了直通标准的延迟和丢失。定义开放和空头标准可能有点棘手,我们很快就会看到。
定义开放标准
图 3 显示了女子公开赛的物理结构。中心导体的左侧是典型的母连接器配置,使用弹簧指
插座。中心导体的右侧保持未连接状态,形成开路。
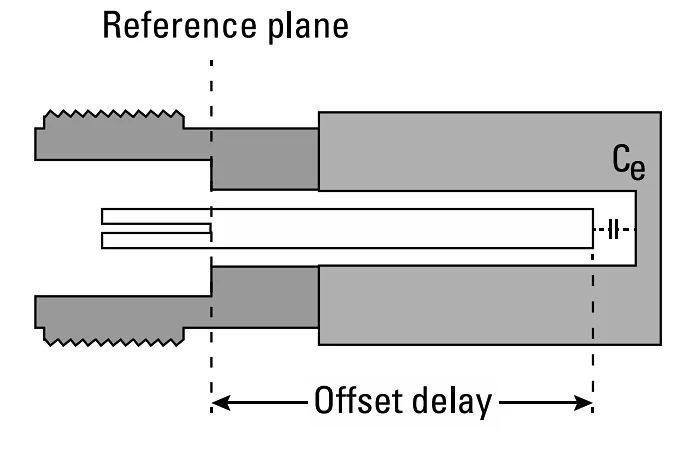
女性开放标准的物理构造。
图 3.女性开放标准的物理结构。图片由Gregory Bonaguide 和 Neil Jarvis提供
请注意,参考平面和 Open 的实际实现之间有很短的传输线。由于传输线增加了延迟,从而在反射信号中产生频率相关的相位,因此该标准可以更准确地称为“偏移开路”。然而,几乎所有开放标准实际上都是偏移开放的,因此通常不值得进行区分。
在内导体和外导体之间的中心导体的开放端处形成边缘
电容(C e )。更复杂的是,该电容还与频率相关。它影响标准的反射系数,不可忽视。
在低频下,固定电容值( C 0 )可能就足够了。对于高于几百 MHz 的频率,电容随频率的变化变得更加明显。大多数 VNA 使用三阶多项式方程来描述边缘电容随频率的变化:
Ce(f) = C0 + C1f + C2f2 + C3f3
等式 2。
系数C 0、C 1、C 2和C 3取决于特定开放标准的几何形状和材料成分。系数应采用适当的单位,以使终值具有法拉单位。例如,如果C 0的单位为飞法,则C 1 的单位应为fF/Hz,C 2 的单位应为fF/Hz 2,依此类推。
图 4 显示了是德科技 VNA 中指定的典型开放标准的参数。
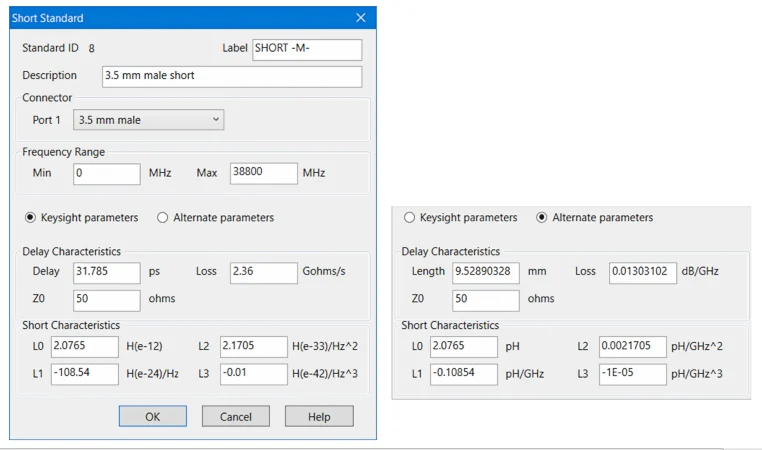
典型开放标准的参数。
图 4.典型开放标准的参数。图片由是德科技提供
正如您所看到的,传输线的参数(延迟、损耗和特性阻抗)与边缘电容的系数一起指定。对于某些校准套件模型,使用相同的三阶多项式和延迟来描述校准标准。套件制造商依靠精密制造和加工来实现这一点。即便如此,某些错误仍然会持续存在。
定义校准标准的另一种方法是使用来自非常校准的 VNA 的反射与频率测量结果的数据库。数据库方法比多项式方法准确得多,但成本也高得多。
史密斯圆图上的开放标准
理想的开路位于史密斯圆图圆周上相位角为零的单点处。然而,如果我们测量给定频率范围内开放标准的反射系数,我们得到的是一条弧,而不是一个点。我们可以在图 5 中看到这一点,它显示了S2611 校准套件的开放标准的测量反射系数。
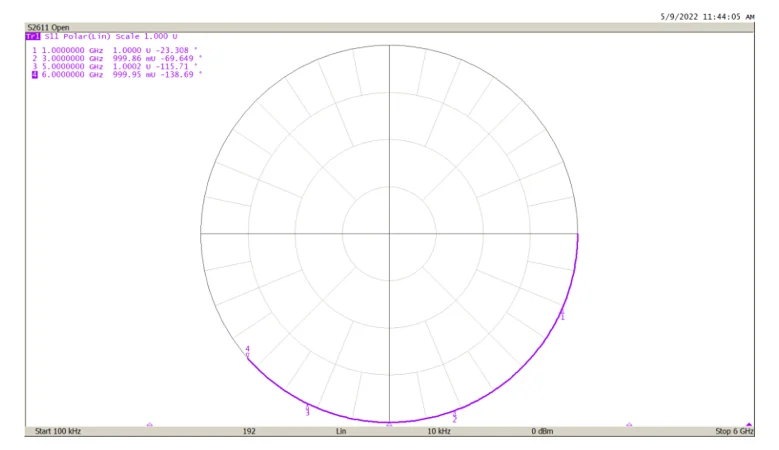
史密斯圆图显示了 S2611 开放标准的反射系数测量值。
图 5.史密斯圆图显示了 S2611 套件开放标准的测量反射系数。图片由铜山技术公司提供
测量的反射系数显示为弧形。当频率较低时,它从零相角开始,然后随着频率增加而顺时针移动。这是由于两个因素:
开路的边缘电容。
实际开路之前出现的短传输线。
定义简短标准
图 6 显示了女性 Short 的物理结构。中心导体与图右侧的外导体短路。
女性 Short 标准的物理结构。
图 6.女性 Short 标准的物理结构。图片由Gregory Bonaguide 和 Neil Jarvis提供
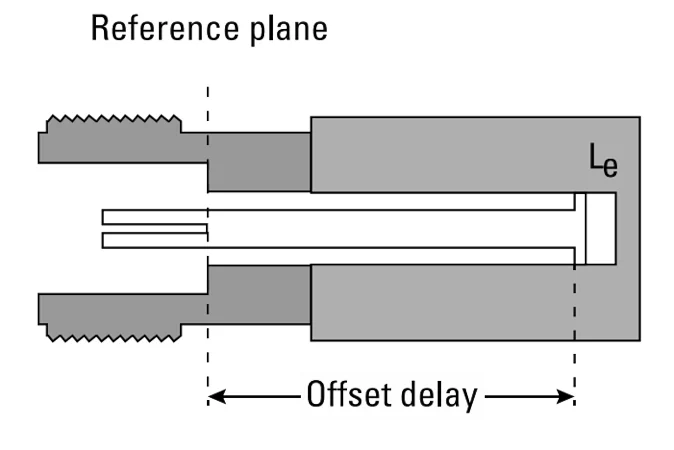
与开放标准一样,在标准实际实施之前有一段较短的传输线。因此,该标准是偏移短路。与公开赛一样,几乎所有 Shorts 都是如此——我们在这里进行区分只是为了解释为什么标准的反射信号会经历与频率相关的相位变化。
在短路位置处会产生一个
电感 ( L e )。与我们在上一节中讨论的边缘电容一样,该电感与频率相关。对于低频和大连接器尺寸(≥7 mm),我们也许可以忽略Le 。在较高频率下,对于小型(≤3.5 mm)连接器,我们至少需要一个三阶多项式来描述电感随频率的变化:
Le(f) = L0 + L1f + L2f2 + L3f3
等式 3。
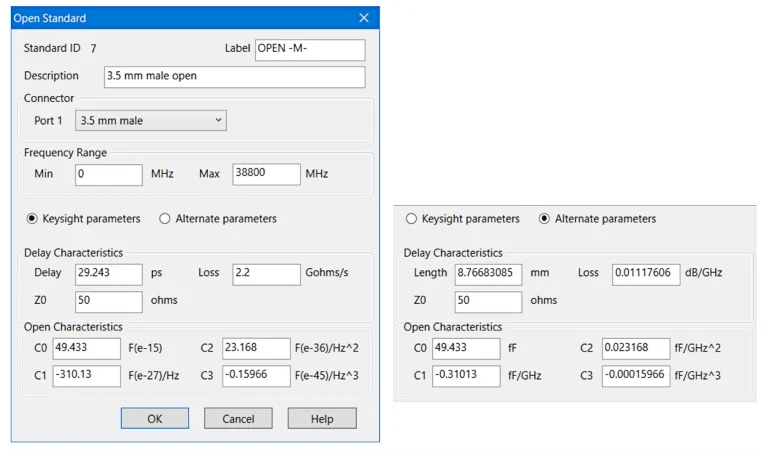
图 7 显示了 Short 标准参数的一些典型值。
典型 Short 标准的参数。
图 7.典型 Short 标准的参数。图片由是德科技提供
史密斯圆图上的短期标准
在史密斯圆图上,测得的短路反射系数显示为一条弧线,该弧线在低频时以 180 度相角开始,并随着频率的增加而顺时针移动。这是由于短路的寄生电感和传输线的长度使其成为偏移短路。图 8 显示了 S2611 校准套件短路的测量反射系数。
史密斯圆图显示了 S2611 短标准的测量反射系数。
图 8.史密斯圆图显示了 S2611 套件的 Short 标准的测量反射系数。图片由铜山技术公司提供

测量校准标准
假设我们在用户校准中使用开路和短路标准。如果我们在校准后使用 VNA来测量这些标准的反射系数,我们还会在史密斯圆图上看到弧线吗?
总之,是的。大多数真实的开盘和空头实际上是偏移开盘和偏移空头,因此它们的响应对应于史密斯圆图上的弧而不是单个点。有关原因的更多信息,请参阅“通过示例学习 - 使用阻抗史密斯圆图”中的示例 4 和 5。
校准过程不会改变这一点。它仅消除测试设置中的缺陷,并确定正确的误差项,以将标准的测量响应映射到三阶多项式描述中预期的响应。事实上,即使标准在某种程度上受到轻微损坏并且没有产生其制造商指定的特性,VNA也会调整结果以使其与其多项式描述一致。
因此,您应该通过测量并非来自校准过程中使用的套件的开路或短路标准来验证已完成校准的结果。此过程会根据标准品的测量响应产生误差项 - 如果我们重新测量同一套件中的标准品,我们可能会错误地认为校准是正确的。VNA 已经过调整以符合该标准的特性。
通过使用不同的标准,我们可以了解 VNA 对不属于校准过程的设备的测量效果如何。这使我们能够发现校准过程中可能发生的任何错误或不一致,例如不正确的标准定义或松动的连接。






