热电冷却器效率和散热器热阻抗

　　热电冷却器 (TEC) 很常见并且（看起来）简单，但简单（且非常准确）的设计模型和方程并不常见。该设计模型在各种应用中表现良好，其输入仅需要典型 TEC 数据表中提供的数字。尽管对 TEC 物理进行了简化，但它足够真实且准确，足以有用。它根据 TEC 数据表参数、驱动电流 (I)、热负载功耗、热导率、散热器热阻抗和环境温度 (T3) 来预测 TEC 热负载温度 (T)。
　　该模型总结为 T = TEC 输出温度的单个二阶方程。

　　T = (-PI + I 2 Rp/2 + Q1)/(C1 + Cp) + Zh(Q1 + I 2 Rp) + T3

　　在哪里：
　　P（瓦/安培）= 珀耳帖常数 = (Qmax + Imax 2 Rp/2)/Imax
　　Qmax（瓦）= 零 Delta T 上的传热（来自 TEC 数据表）
　　Imax = 完美 (Zh = 0) 散热器的冷却电流（来自 TEC 数据表）
　　Vmax = Imax 时的 TEC 压降（来自 TEC 数据表）
　　Rp = TEC 电阻 = Vmax/Imax
　　Q1 = 热负荷产生的热量
　　C1 (W/°C) = 热负载到环境的导热系数
　　Cp = TEC 热导率 = Qmax/DeltaTmax
　　DeltaTmax = 使用 Imax 和完美散热器的冷却（来自 TEC 数据表）
　　Zh ( o C/W) = 散热器对环境的热阻
　　T3 = 环境温度
　　有关此数学如何应用于实际 TEC 的典型示例，请考虑 Laird Thermal Systems 430007-509：
　　Q：3W
　　电流：1.5A
　　电压：3.4V
　　温差：67°C
　　然后：
　　RP = 3.4/1.5 = 2.27
　　P = 3 + 1.5 * 3.4 / 2 = 5.55 / 1.5 = 3.7 瓦/安
　　Cp = 3 W/67°C = 0.0448 W/°C
　　通过设计模型数学量化的有用关系是散热器热阻抗对产生冷却效果的 TEC 驱动电流的影响。当 T 方程相对于 I 进行微分，然后求解 dT/dI = 0 处的值时，就会得到结果。它产生：
　　Io = (P Zh -1 )/{Rp[Zh -1 + 2(C1 + Cp)]}
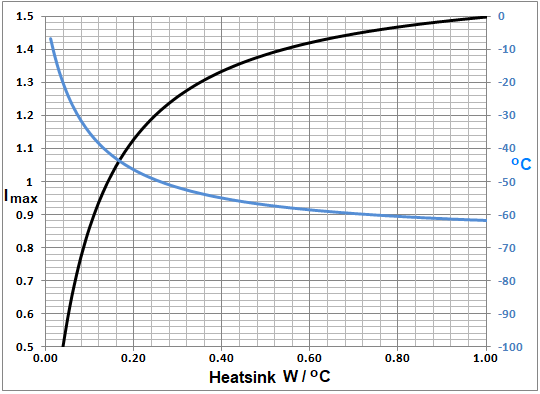
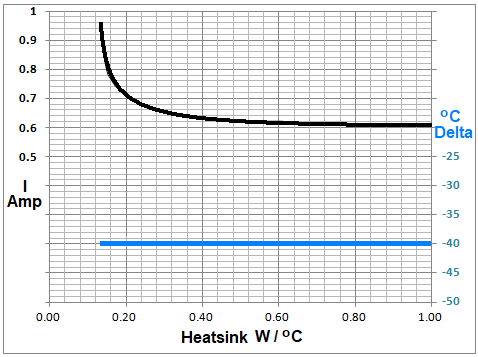
　　图 1中绘制了莱尔德 TEC 的Io(Zh -1 ) （黑色）和相应的 Delta T（蓝色）。请注意，随着 Zh -1的减小，两条曲线都趋向于零。这种效应主要是由于以下事实：TEC 耗散的 I 2 Rp 热量必须通过散热器排放到环境中，这会提高其温度，从而提高 TEC 的温度，与 Zh 成正比。

　　图 1 TEC 冷却驱动电流（黑色）和终冷却（蓝色）作为散热器热导纳 (Zh -1 ) 的函数。
　　即使在 TEC 冷却能力保持足够且 DeltaT 恒定的情况下，对 TEC 电流消耗和功耗的影响也是巨大的，如图2中 40 o C的 DeltaT 示例（Q1 和 C1 = 0）所示。

　　图 2恒定 40°C DeltaT 下的TEC 电流消耗 I（黑色）与散热器热导纳 (Zh -1 ) 的关系。
　　请注意，当 Zh -1从 1.0 下降到 0.13 W/°C时，电流消耗增加 63%，功率增加 165% 。