468-4 频谱简介
图 1 显示了 ITU 文档“声音广播中音频噪声电压电平的测量”中指定的频率响应。
468-4 加权噪声滤波器的频率响应
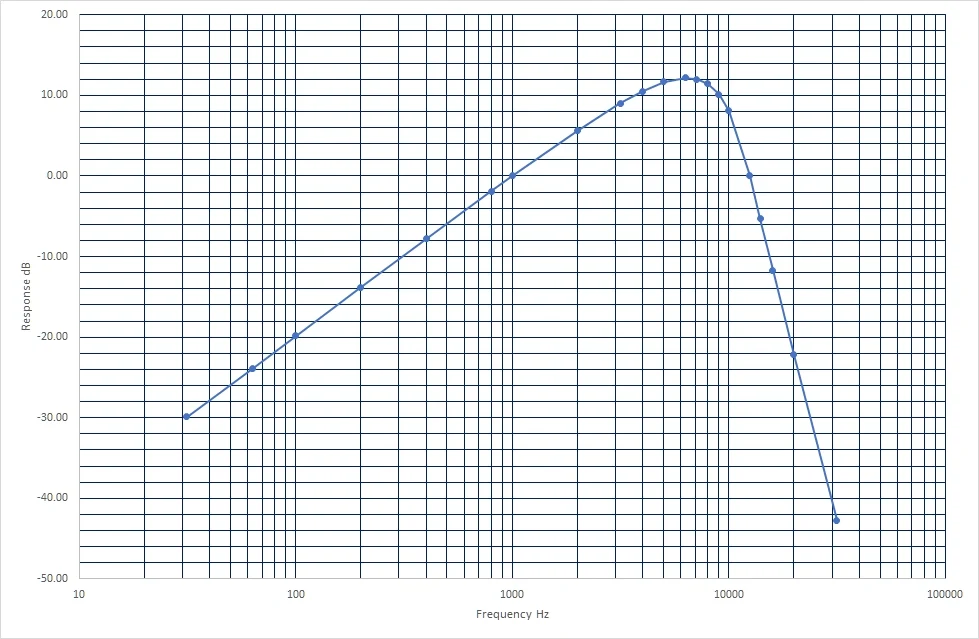
图1。468-4 加权噪声滤波器的频率响应
曲线的上升部分的梯度为6dB/倍频程,因此它是一阶高通部分。下降部分的梯度为-30 dB/倍频程,使其成为五阶低通部分。
原创无源滤波器解决方案
ITU文件还包括图2所示的无源滤波器电路。该电路可以实现期望的响应。该文件还指出,电感器在 10 kHz 时的 Q 值必须至少为 200,并且可能需要对 C3 的值进行一些调整,以满足曲线的指定容差限制。(我们稍后将讨论公差。)
用于 600 Ω 电路的 468-4 滤波器的无源网络实现

图2 . 用于 600 Ω 电路的 468-4 滤波器的无源网络实现
图 2 的滤波器电路初开发于 20 世纪 60 年代末,基于 1950 年代初的更早工作,当时广播音频互连技术仍然主要基于 600 Ω 迭代匹配。图 2 的无源网络具有显着的插入损耗,因此需要额外的
放大器才能在 6.3 kHz 下实现 468-4 滤波器指定的 12.2 dB 增益。
现代音频系统要求
如今,600 Ω 匹配已不再使用。相反,音频信号源设计为具有 100 Ω 或更小的源电阻,输入设计为具有 10 kΩ 或更大的阻抗。
有两种主要方法可以制作满足这些阻抗目标并提供 468-4 频率响应的有源滤波器:
合并 6.3 kHz 左右的传统低通和高通有源滤波器。
使用巧妙的数学技术从无源电路导出有源电路。
本文的其余部分将介绍种方法。不幸的是,这个过程并不容易,至少部分问题在于原始频率响应规范和指定的容差。
分析 468-4 噪声过滤频谱
频率响应规格可能是通过测量实际网络获得的,该网络会受到随频率非线性变化的电感器损耗的影响。这不能通过在有源滤波器技术中添加串联和并联
电阻器或等效物来建模。
即使线性模型也很复杂。其频率响应的一个公式表明,涉及六阶和五阶低通响应之和,尽管五阶响应在约 16 kHz 以上占主导地位,如 30 dB/十倍频程的梯度所示。无需六阶滤波器也可以满足规格,但在滤波器效果的地方容差较小。
一阶高通和五阶低通滤波器的电路是众所周知的;的问题是确定滤波器部分的临界频率以及五阶滤波器是否可以平坦。临界频率f是响应为-3dB时的频率。
这绝不是一件简单的事情:高通部分的临界频率所需值取决于低通滤波器响应的形状,并且简单的试验设计表明,该滤波器的两个部分都不是平坦的或平坦的。类似于任何其他“标准”响应(切比雪夫、贝塞尔等)。
简单的“尝试”调整要在可接受的时间内产生良好的结果,变量太多,因此有必要使用优化应用程序。
作者注:我感谢 LTspice 用户组 (LTspice@groups.io) 的成员 Tony Casey 在使用Microsoft Excel 的 Solver 插件来 帮助求解这些方程方面提供帮助。
用于 468-4 噪声过滤的有源滤波器设计

图 3 提供了两个原理图:(顶部)添加了通用
运算放大器以补偿插入损耗的原始无源滤波器,以及(底部)优化的有源滤波器。
无源滤波器和优化后的有源滤波器仿真示意图

图3 . (上)无源滤波器的仿真原理图和(下)优化的有源滤波器
阻力值是由优化器计算的值。为了达到所需的电阻,我组合了两个容差为 1%的 E12 值电阻。为了支持微调,遵循以下三个步骤:
选择一个接近目标值的电阻。
如果电阻值低于目标值,请串联添加一个小值电阻。
如果电阻值高于目标值,请并联一个大值电阻。
对于有源滤波器部分,个放大器输出端的C 2和R 2形成一阶高通滤波器。R 3和C 3形成五阶Sallen 和Key 滤波器的一阶低通部分。缓冲器U 1和U 3将滤波器部分与周围的源和负载阻抗隔离,因为响应必须非常准确。
U 4周围的电路是两个二阶部分之一,U 5周围的电路是另一个二阶部分。R 11的值至关重要。必须将其调整为R 10测量值的1.413倍。
468-4 加权噪声滤波器设计的仿真 我使用 LTspice 模拟了图 3 的设计。图 4 显示了有源滤波器部分的分离频率响应。整体 5 阶低通滤波器响应略有峰值,但第三部分(即二阶部分)本身就相当峰值,这就是为什么R 11的值至关重要的原因。
各个有源滤波器部分的频率响应
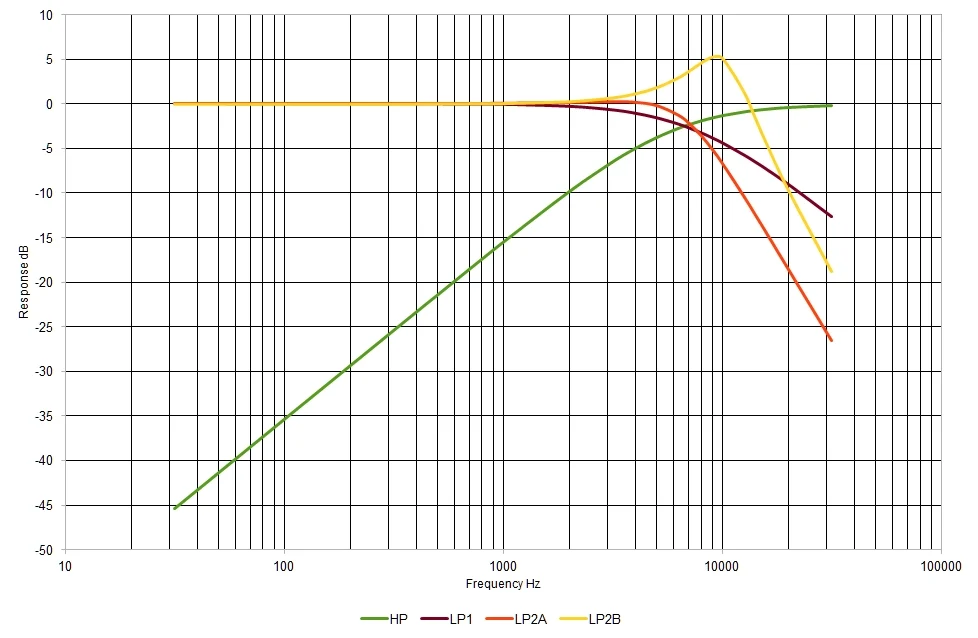
图4 . 各个有源滤波器部分的频率响应
图 5 将图 3 有源滤波器响应与规格容差进行了比较。请注意,6.3 kHz 处的容差为零,因为这是设置滤波器增益的参考频率。

模拟滤波器响应偏差和指定的公差
图 5.模拟滤波器响应偏差和指定容差
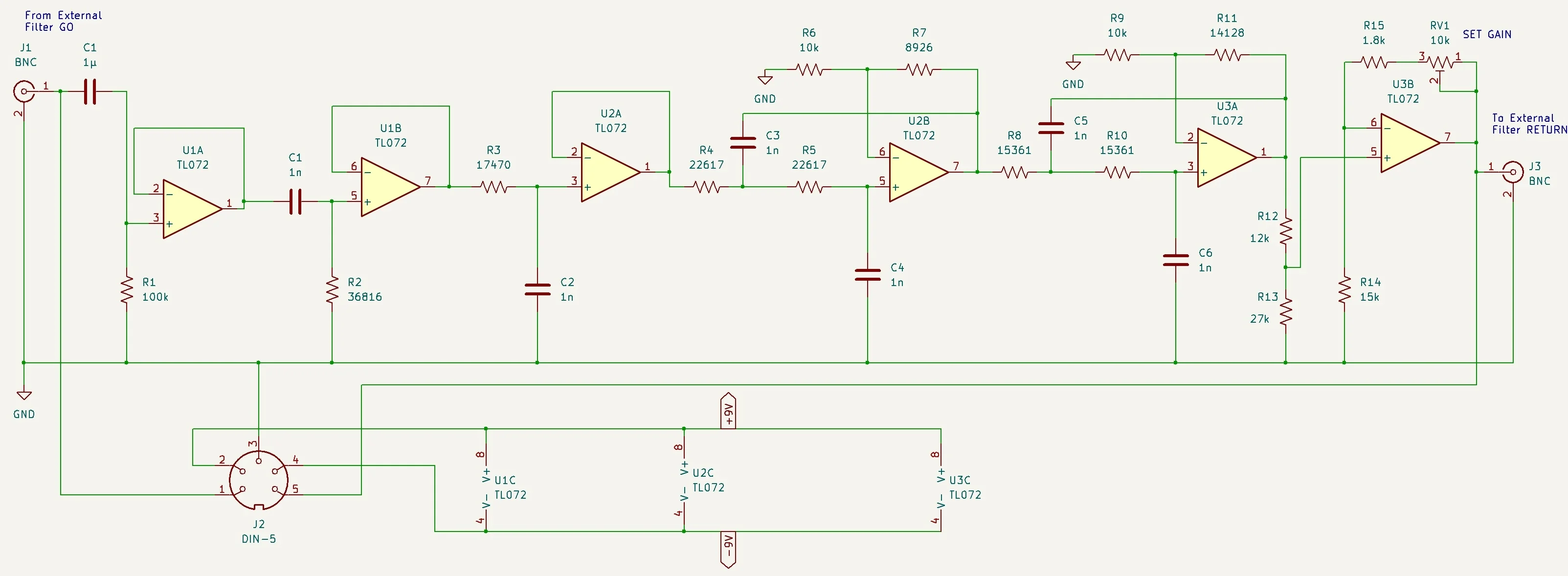
构建并测试 468-4 加权噪声滤波器

图 6 显示了所构建的滤波器的示意图。
构造的过滤器示意图
图6 . 构造的滤波器示意图(点击放大)
电阻器R 2、R 3、R 4、R 5、R 8和R 10设置滤波器部分的临界频率,以及 1 nF
电容器的实际值,在任何情况下,这些值都应尽可能接近你能承受的宽容。
如果您可以测量以皮法为单位的电容器值,则可以使用以下公式调整每个电阻器值,以考虑与其连接的电容器的实际值 C:
R = R s c h × ( 1000 C)
其中Rsch是原理图中的电阻值。此调整对电路进行补偿,以实现所需的 -3 dB 频率,该频率由下式给出:
f 3 d B = 1 2 π R C
U3B运算放大器周围的电路需要一些解释。U3A运放输出的增益变化 不太可能超过±1 dB,但为了安全起见,我们将使用
电位器R V1进行±2 dB的调节范围。然而,是非反相的,因此它的增益不能小于 1。
为了克服这个问题,R 12和R 13形成3 dB衰减器,而R 14和R 15与R V1给出1 dB至5 dB的增益调节范围。当R V1设置为 4.4 kΩ 时,增益为 3 dB ,相当接近中间值。
图 7 显示了所构造滤波器的响应误差曲线与指定容差的比较。
构造的滤波器响应偏差和规定的公差
图 7 . 构造的滤波器响应偏差和规定的公差
将滤波器连接到我的宽带电压表
在我之前的噪声滤波器项目中,我将滤波器设置为 1 kHz。对于此,需要通过调整R V1进行调整,以在 6.3 kHz 处实现 12.2 dB 增益。图 8 显示了连接到我的宽带电压表时测得的滤波器频率响应。
F连接了 468-4 滤波器的宽带电压表的频率响应

图 8 . 连接 468-4 滤波器的宽带电压表的频率响应
正如我们在本系列中所看到的,选择滤波器来测量噪声可能是主观的,就像我们个人的听力反应一样。在这种情况下,468-4 滤波器的设计旨在近似噪声对音频广播信号的影响。其成形带通响应并不能告诉我们信号中有多少噪声,但在特定应用中可能更有用。








