这是石英晶体的等效电路:
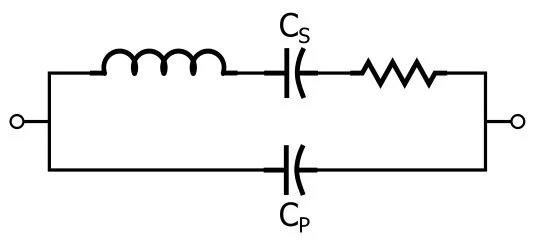
让我们明确一点:石英晶体就是石英晶体。如果你用锤子敲击晶体,它不会损坏电感器、
电阻器和两个
电容器。然而,石英晶体具有(在我看来相当神秘的)机电特性,这些特性导致晶体在
电子电路中表现出类似上面所示的无源元件集合的行为。
等效电路中的所有这些元件都非常常见。那么,您可能想知道为什么我们要费心使用石英晶体。为什么不在同一排列中使用电容器、电感器和电阻器呢?好吧,正如我们稍后将看到的,使用无源器件永远无法实现同等性能,尤其是当您考虑到石英晶体有多小时。
谐振
电感器和电容器储存能量。如果以允许能量在两个组件之间来回流动的方式连接电感器和电容器,就会形成谐振电路。在理想化电路中,这种来回流动永远持续下去,并且您将拥有一个振荡器。在现实电路中,随着能量被电线或 PCB 走线等电阻元件耗散,振荡幅度会减小(并终停止)。阻力越大意味着振荡更加“阻尼”,即振幅下降得更快。Q 因子与电阻成反比,这意味着 Q 值越低,振荡消失得越快。
串联 LC 电路和并联 LC 电路都会发生谐振,如果您回顾等效电路,您会发现晶体同时具有串联谐振和并联谐振。串联电感和电容的谐振频率遵循标准公式:
fSR=12π√LCS
并联谐振有点复杂。该谐振频率计算如下:
fPR=12π√L(CSCPCS+CP)
然而,事实证明 C P比 C S大得多(可能大 2000 倍),这意味着 C S C P /(C S + C P ) 大约等于 C S C P / C P。然后我们取消 C P项,剩下
fPR\约12π√LCS \右箭头 fPR\约fSR
所以这两个谐振频率非常接近。当您购买晶体时,它会指定特定的频率。出于所有实际目的,我们可以说晶体的工作频率等于 f SR。
(极高)Q值
如上所述,您不能仅用等效的无源元件集合来替换晶体。为什么?好吧,你需要一些足够大的 PCB 空间来匹配晶体的电感——我的教科书说它可能高达数百亨利,而我发现这个 StackExchange 线程有人说它可能高达数千亨利。Digi-Key 销售的
固定电感器为 150 亨利;它的电阻为 3.7 kΩ,重量为半磅,宽度超过两英寸。此外,晶体的大电感与相对较小的电阻相结合,从而产生非常高的 Q 因数。
频率响应
如您所知,电感器和电容器具有电抗。石英晶体也有电抗,但由于三个电抗成分之间的相互作用,该电抗有点复杂。
在低频下,容抗占主导地位。
随着频率增加,电抗幅度减小,终在 f SR处达到零(正如预期的那样,串联 LC 电路在谐振频率下具有零阻抗)。
当电抗在 f SR处过零后,它会迅速增加到无穷大,因为 f PR略高于 f SR并且理想并联 LC 电路的阻抗在谐振频率处为无穷大。
使其振荡
石英晶体是晶体,而不是振荡器。为了产生振荡,晶体必须集成到具有振荡器电路所表现出的典型特性(即放大和反馈)的电路中。如果您查看经典振荡器拓扑(例如 Colpitts 或 Hartley),您会看到放大器(例如 BJT)、LC 储能电路(用于提供谐振)和反馈连接 - 例如,在 Colpitts 振荡器中,反馈从储能电路中两个电容器之间的节点传送到 BJT 的发射极:
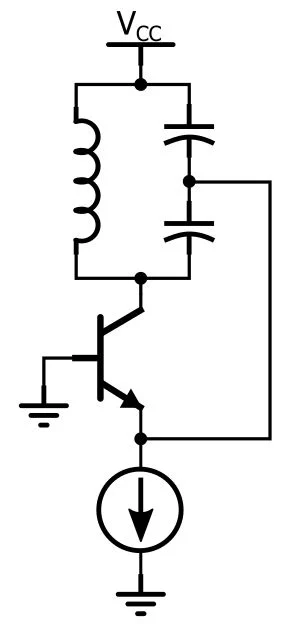
总体思路与基于石英的振荡器相同,因为石英晶体本质上是一种非常高性能的谐振元件。皮尔斯(或皮尔斯-门)振荡器是用于产生数字振荡的常见拓扑;它看起来像这样:

您可能会花费相当长的时间来尝试彻底分析和理解这个看似简单的电路的所有细节。如果您想更深入地了解皮尔斯拓扑和基于晶体的振荡,我认为文章“皮尔斯门
晶体振荡器简介”(为微波产品文摘撰写)将是一个很好的起点。
结论
我希望您现在对 1) 电子学中的石英晶体是什么以及 2) 石英晶体的特性与正确设计的电路结合使用时如何导致振荡有更清晰的了解。


