为了获得更深入的了解,让我们进行一些模拟并检查
二极管解调器的操作。假设我们有 V EXC = 4sin(2π x 2500 xt)。另外,假设在零位,V s1 和V s2的幅值都等于4V;然而,由于给定的磁芯位移,两个次级绕组上的电压将变为:
V s1 = 4 x (1+0.3) x sin(2π x 2500 xt)
公式1
V s2 = -4 x (1-0.3) x sin(2π x 2500 xt)
公式2
这里,我们假设次次级的幅度与零位幅度相比增加了 1.2 V;第二个次级的幅度也减少了相同的值 (1.2 V)。我们可以使用下面的 LTspice 原理图来模拟这个示例:
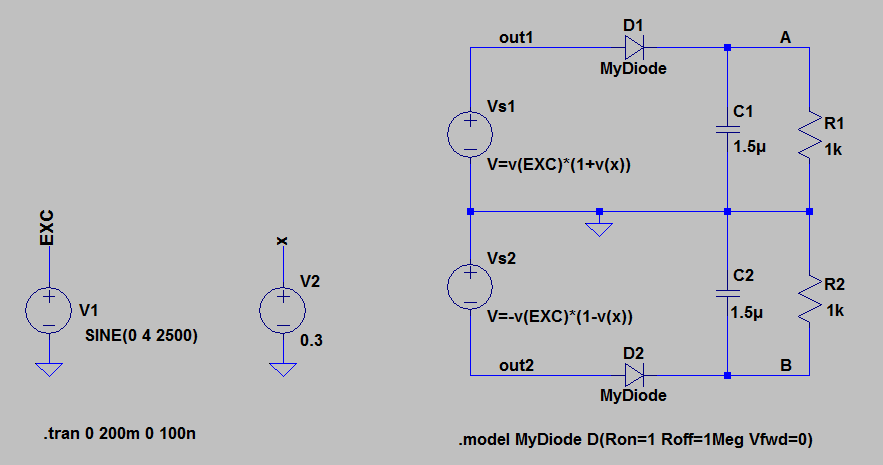
图3
在此原理图中,电压源 V s1和 V s2是 LTspice“任意行为电压源”,用于产生等式 1 和 2 给出的电压。例如,V s1等于节点 EXC 处的电压,v( EXC),乘以因子1加上节点x处的电压,即1+v(x)。节点EXC的电压为激励电压,节点x的电压为0.3。由此得出 V s1 = v(EXC) x (1+0.3) = (1+0.3) x 4 x sin(2π x 2500 xt),与公式 1 相同。
二极管 D1 和 D2 是LTspice .model 语句定义的理想二极管。当 R=1 kΩ 且 C=1.5 μF 时,我们得到上半波整流器的以下波形:
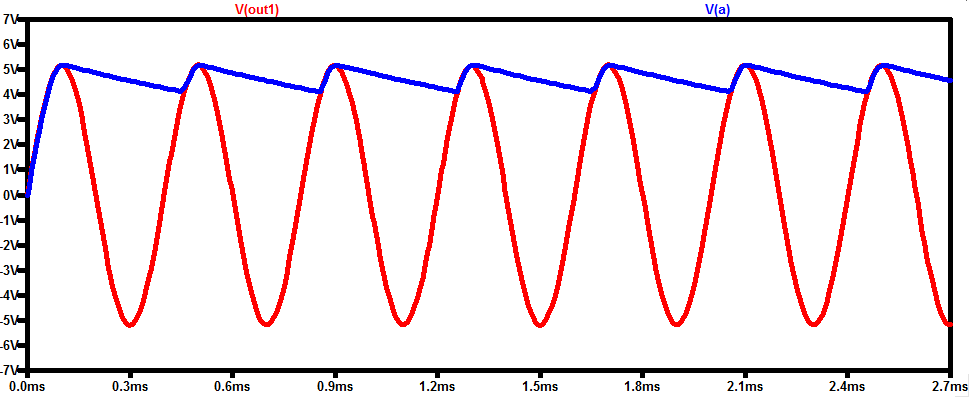
图4
忽略电压纹波,节点 A 的直流值为约 4.66 V。对于下部整流器,我们得到以下波形。
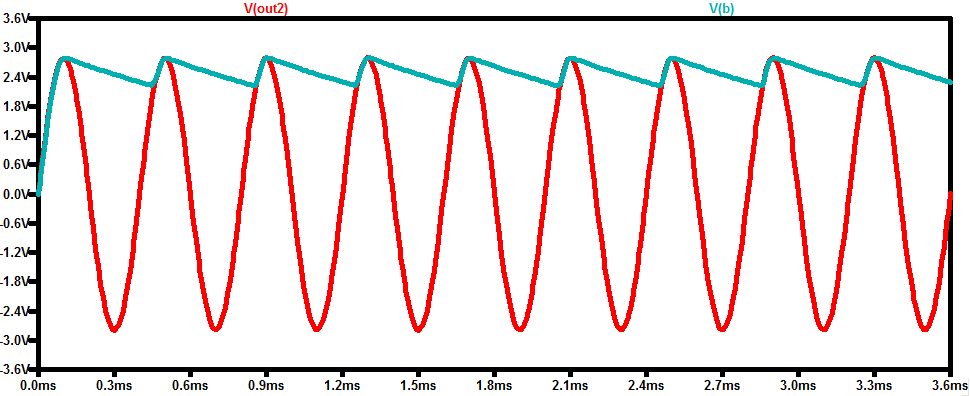
图5
节点B的DC值如预期较小(约2.51V)。输出是这两个直流电压之间的差,并且具有大约2.15V的直流值。输出的幅度与磁芯位移量成正比。考虑到输出的极性,我们知道 |V s1 | > |V s2 |。这揭示了位移的方向。
模拟机械带宽为 250 Hz 的系统
现在,我们假设附着在上的物体的运动具有 250 Hz 的正弦波形,来检查上述系统:
运动 = 位移 x sin(2π x 250 xt)
由于 LVDT 输出的幅度随磁芯位置线性变化,因此我们得出结论,V s1和 V s2可以用以下等式表示:
V s1 = 4 x (1+x) x sin(2π x 2500 xt)
公式3
V s2 = -4 x (1-x) x sin(2π x 2500 xt)
公式4
其中 x 是 250 Hz 的正弦曲线。假设对于给定的 LVDT,x 的幅度为 0.3。因此,我们有
x = 0.3 x sin(2π x 250 xt)
我们可以使用下面的 LTspice 原理图来模拟这个示例:

图6
除了V s1和V s2的幅度变化遵循正弦波形(v(x)=0.3×sin(2π×250×t))之外,这与前面的示例相同。节点 out1 和 A 处的电压如下所示。
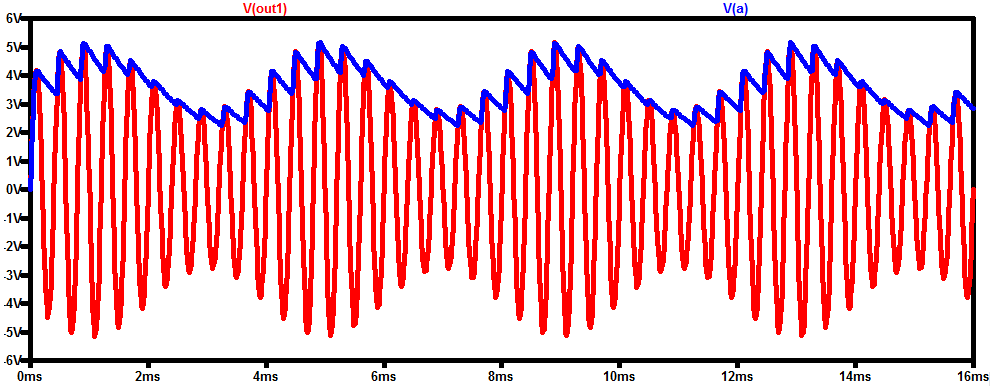
图7
正如您所看到的,次级两端的电压是一个正弦波形,其幅度由磁芯位置调制(在我们的模拟中,幅度实际上由 x 调制,假设 x 是磁芯位置的函数)。这就解释了为什么用于提取位置信息的电路被称为解调器。
对于下部整流器,我们得到类似的波形,如图 8 所示。
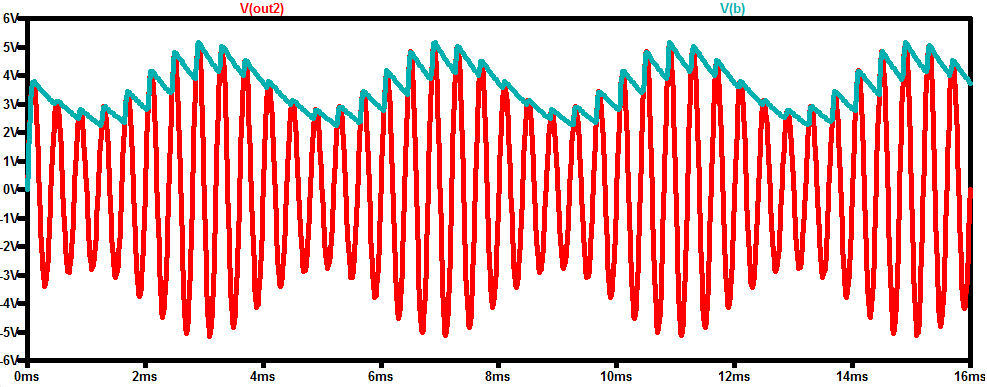
图8
下图中的红色曲线显示了终的输出(V out = V(a)-V(b))。
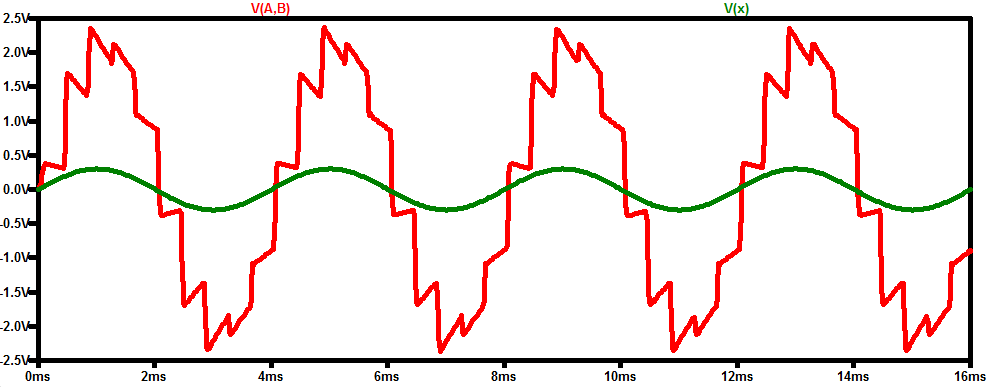
图9
尽管输出信号有一些突变,但它看起来像是 x 的放大版本,它是位移的函数。
因此,调制器输出似乎为我们提供了预期的位置。为了验证这一点,我们可以使用 LTspice 的 FFT 功能来查找输出电压的频率内容。如图 10 所示。
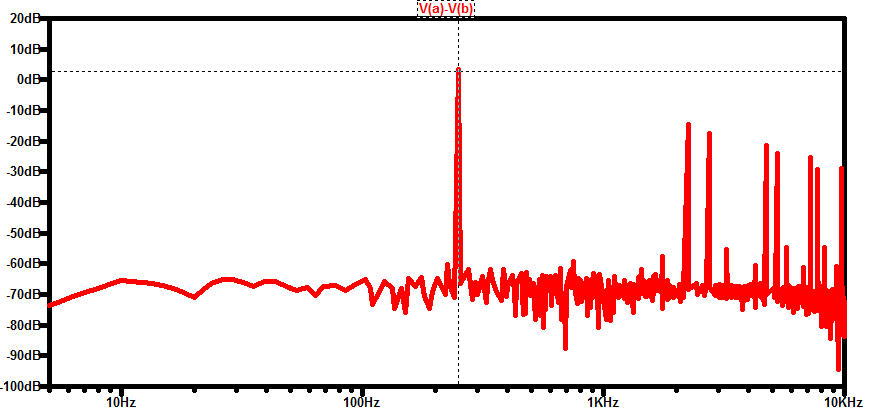
图10
输出 FFT 显示主要频率分量位于 250 Hz,这是物体运动的频率。还有一些高频分量可以通过信号调理电路后续级中的低通
滤波器进行滤除。
二极管半波整流器的局限性
上述模拟结合了理想二极管模型。现实世界的二极管表现出非零正向压降。在 LVDT 输出幅度相对较小的情况下,这可能会导致非线性误差。为了避免二极管 IV 特性的非线性区域,即使磁芯处于距零位的距离时,LVDT 次级的幅度也应大于二极管的正向压降。
请记住,当磁芯处于满量程位移时,次级
线圈之一的电压处于值。对于某些微型和特种 LVDT,输出幅度可能相对较小,并且二极管正向电压可能会导致问题。
此外,二极管的正向压降是温度的函数(硅的温度系数约为 -2.2 mV/°C)。正向压降甚至会随着焊接过程引起的机械应力而变化。另一种可能导致机械应力的机制是二极管本体和电路板之间的热膨胀系数差异。因此,为两个 LVDT 输出提供充分匹配的整流器可能具有挑战性。
除了二极管的正向压降之外,两个路径的阻抗也应该匹配,以避免两个次级响应之间出现不必要的不??匹配。
精密整流器
为了规避二极管整流器的限制,我们可以使用精密整流器(如图 11 所示)来获取每个 LVDT 次级的直流值。
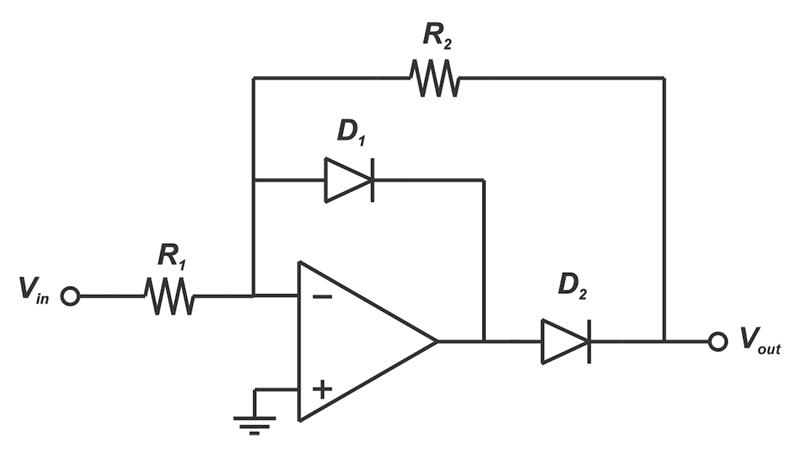
图11
尽管精密整流器可以克服简单二极管整流器的挑战,但它也有其自身的局限性,例如噪声抑制能力很小。在下一篇文章中,我们将更详细地了解该电路并讨论 LVDT 应用的同步解调器。








