基尔霍夫电压定律
基尔霍夫电压定律指出,环路中所有电压的代数和必须等于零。该定律的实际应用是分压器,如下图所示。
如果U 1是9V
电池,R 1是3欧姆电阻,R 2 是6欧姆电阻,则电路中流动的电流为
$$\frac{9 \text{ v}}{3 \text{ } \Omega + 6 \text{ } \Omega} = 1 \text{ A}$$。
R 1两端的电压将为
$$ 3 \text{ }\Omega \text{ x } 1 \text{ A} = 3\text{ v}$$,
R 2两端的电压为
$$ 6 \text{ }\Omega \text{ x } 1 \text{ A}= 6\text{ v}$$。
各个
电阻器两端的电压等于两个电阻器两端的电压乘以各个电阻与总电阻的比率。用于计算电阻器 R 2、U 2两端电压的公式也如下所示。
分压器
图1 分压电路
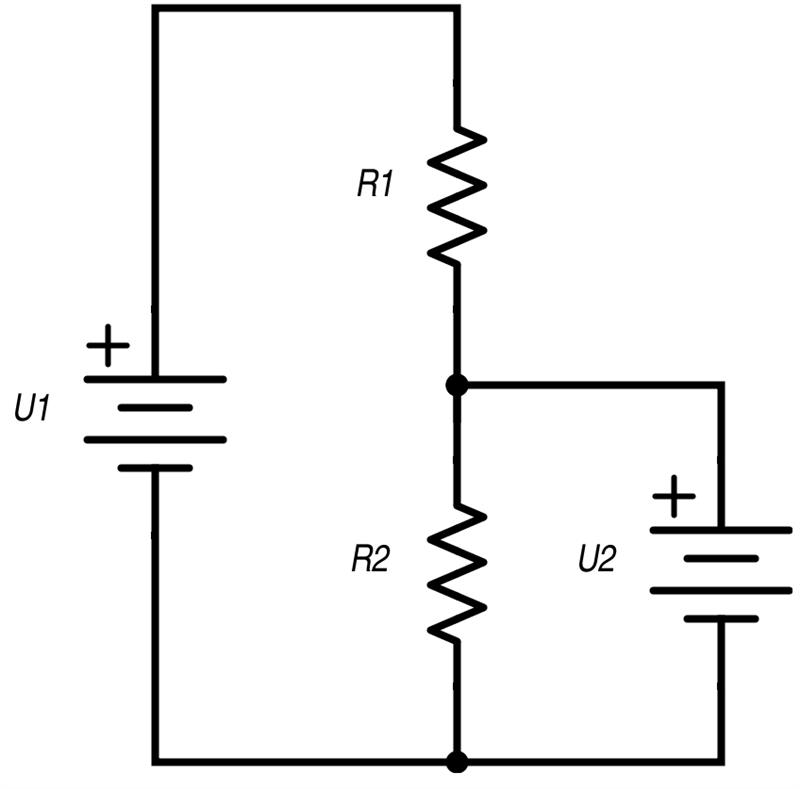
$$U_{1}=\frac {U_{1}R_{2}}{R_{1}+R_{2}}$$
基尔霍夫电流定律
同样,您可以划分电流。支配这一现象的定律称为基尔霍夫电流定律。该定律规定:“进入和离开节点的所有电流的代数和必须等于零。”
要了解其工作原理,请参阅下图。I T是提供给四个并联电阻电路的总电流。I X是将流过 R X的电流。如下式所示,流过 R X的 I T部分将等于 I X乘以 R X与总电阻的比率。如果所有电阻器的值相同,则通过每个电阻器的电流将相同。
例如,如果 $$I_{T} = 1 \text{ A}$$ 且 $$R_{X}=R_{1}=R_{2}=R_{3}=30 \;\Omega$$,
那么 $$R_{T} = 10 \;\Omega$$ 和 $$I_{X} = \frac{I_{T}R_{T}}{R_{X}+R_{T}} = \frac{ (1)(10)}{30+10} = \frac{10}{40} = 0.25 \text{ A}$$。
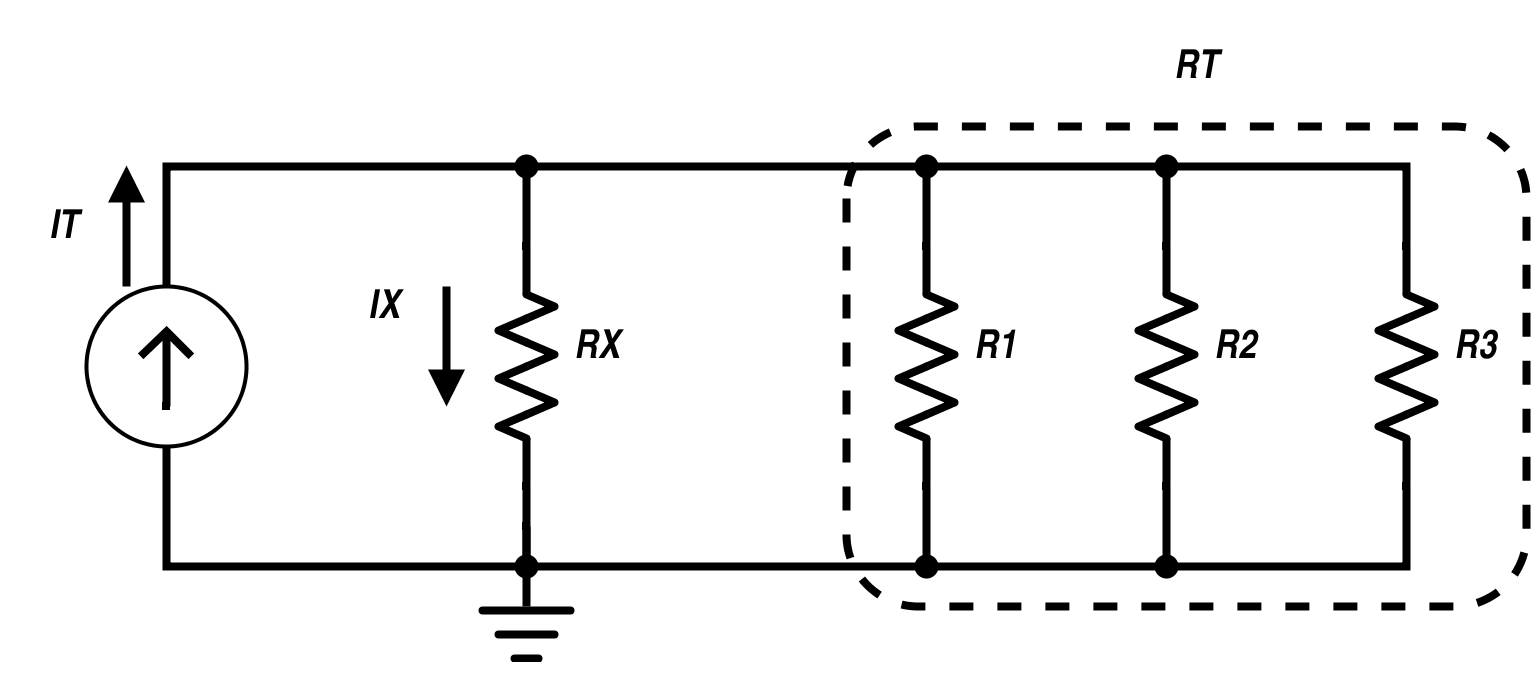
分流器 图2 分流电路
I X = I T R T R X + R TI
分压器和分流器的应用
分压器和分流器有许多实际应用。例如,在下面所示的电路中,R 2是
光敏电阻,其值随着照射到其上的光强度的变化而变化。R 2、U 2两端的电压是光强度的量度。您可以用它来感测阳光的水平,或者
光源和光敏电阻之间是否存在物体。当然,分压器和分流器电路还有许多其他应用。
分压器应用
图 3 分压器应用
U 2 = U 1 R 2 R 1 + R 2

