传输线输入反射系数
为了更好地理解基于传输线的阻抗匹配,重要的是要了解当我们沿着终止于给定负载阻抗 Z L的传输线移动时输入阻抗和反射系数如何变化。请考虑以下图 1 中的图表。
显示负载阻抗和反射系数的传输线的图。
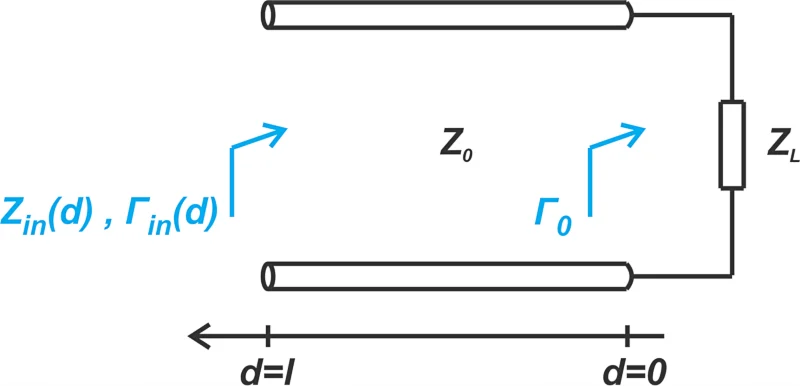
图 1. 显示负载阻抗和反射系数的传输线的图。
可以看出, (d)中距负载距离 d 处的反射系数 Γ 由下式给出:
Γin(d)=Γ0e2βd
等式 1。
在哪里:
β 是相位常数
Γ 0 为负载反射系数
Γ0=
ZLZ0
ZL+Z0
等式2。
公式 1 显示了反射系数如何沿线变化 - (d)中Γ 的大小是恒定的并且等于 Γ 0的大小- 然而,其相位角随着距负载的距离 (d) 线性变化。
接下来,我们来看一个例子。
示例 1:求输入阻抗和反射系数
求 50 Ω 线路的输入阻抗和反射系数,βd = 71.585°,终端负载阻抗为 Z L = 100 + j50 Ω。
通过应用公式 2,我们首先找到负载端的反射系数:
Γ0=0.4+j0.2=0.447\测量角度26.57
图 2在史密斯圆图上找到了 Γ 0(归一化阻抗为 Z 0 = 50 Ω)。

史密斯圆图显示 Γ0 和 Z0 = 50 Ω 的归一化阻抗。
图 2. 史密斯圆图显示 Γ 0和 Z 0 = 50 Ω 的归一化阻抗[点击图像放大]。
在此示例中,βd 参数(称为线路的电气长度)为 71.585°。由式1可知,(d)中的γ的相位角为γ 0的相位 减去2×71.585=143.17°。因此,(d)中Γ 的相位角为 26.57° - 143.17° = -116.6°。
图 2 显示了如何使用史密斯圆图从 Γ 0以图形方式获得 (d)中的Γ ;对于给定的Г 0 ,(d)中沿传输线Г的反射系数位于半径为|Г 0 |的圆上。一般来说,远离传输线上的终端会产生沿着常数 |Г| 的顺时针旋转。圆圈。电长度为 θ 的线会导致史密斯圆图上旋转 2θ。
关于阻抗和传输线的两个重要观察
考虑一条电气长度为 180° 的线路(对应于 d = λ / 2)。这样的线产生完整的 360° 旋转,并将我们移回到我们开始的原始负载阻抗 Z L 。这意味着我们沿着传输线观察到的阻抗每半个波长就会重复。
图 2 还暗示了传输线的一个重要特性;传输线可以将我们从一个恒定电阻的圆移动到另一个。在上面的例子中,一条 71.585° 的长线将我们从 r = 2 的恒阻圆移动到 r = 0.5 的圆。这意味着传输线可以充当阻抗匹配组件。我们很快就会回到这个例子,并更详细地讨论基于传输线的阻抗匹配技术,但在深入讨论之前,让我们首先了解一下史密斯圆图的波长范围。
史密斯圆图波长标度
如上所述,传输线的输入阻抗可以通过史密斯圆图上的简单圆周运动找到。我们还可以使用物理长度来表征线路,而不是使用线路的电气长度,物理长度通常表示为波长的一部分。
该等价的控制方程为 βd = \frac{2πd}{λ}。例如,45°、90°、135°和180°的βd值可以分别由以下物理长度产生:
λ/8
2λ/8 = λ/4
3λ/8
4λ/8 = λ/2
这就是为什么史密斯圆图通常会沿着图的周边提供波长刻度,如图 3 所示。
史密斯圆图示例,其周边带有波长刻度。
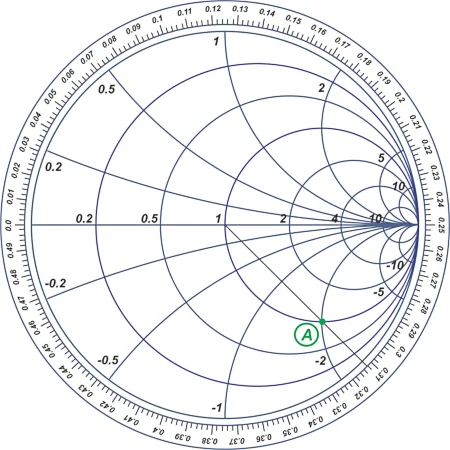
图 3. 史密斯圆图示例,其周边带有波长刻度 [单击图像放大]。
波长标度指定史密斯圆图上每个点的距离为 d。例如上图中的A点对应的距离约为0.312λ。请注意,波长刻度上显示的并不重要;我们主要使用这个比例来计算传输线上两点之间的波长距离。
下面,我们将通过一个示例来阐明如何使用波长尺度来解决传输线问题。在继续之前,请注意,由于 βd = 180°(对应于 d = λ / 2)的电长度会在史密斯圆图上产生完整的 360° 旋转,因此史密斯圆图的波长刻度范围为 0 到 0.5λ。
示例 2:使用波长标度解决传输线问题
假设距负载阻抗 Z Load的距离为 l 1 = 0.051λ ,输入阻抗为 Z 1 = 50 - j50 Ω(下图 4)。

显示示例传输线的距离、负载和输入阻抗的图表。
图 4. 显示示例传输线的距离、负载和输入阻抗的图表。
求 Z Load 以及 距Z 1 l 2 = 0.074λ 处的输入阻抗 Z 2。假设两条线路的特性阻抗均为 50 Ω。
使用 50 Ω 的归一化阻抗,Z 1的归一化值为 z 1 = 1 - j,位于下面的史密斯圆图中(图 5)。

史密斯圆图显示 50 Ω 的归一化阻抗。
图 5. 史密斯圆图显示 50 Ω 的归一化阻抗 [点击图像放大]。
我们知道,沿着传输线移动会导致沿着常数 |Г| 的运动。史密斯圆图上的圆圈。我们只需要确定正确的运动方向即可。请记住,远离终端会产生顺时针旋转(相对于终端),靠近终端会导致逆时针旋转。
如上图所示,z 1 对应波长尺度上的约0.338λ。对于 z 2 ,我们 又偏离 z Load 0.074λ。因此,z 2 对应于波长尺度上的 0.338λ + 0.074λ = 0.412λ,如图 5 所示。另一方面,为了定位 z Load,我们应该沿逆时针方向走,这会导致我们到达对应的点至 0.338λ - 0.051λ = 0.287λ。从史密斯圆图中,我们得到 Z Load = 50 × z Load = 100 - j50 Ω 和 Z 2 = 50 × z 2 = 25 - j25 Ω。
示例 3:求 Z载荷 和 Z 2
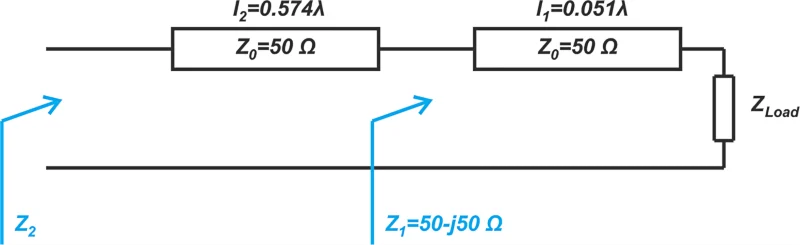
在下图中,Z 1 = 50 - j50 Ω、l 1 = 0.051λ 和 l 2 = 0.574λ。找到 Z负载 和 Z 2。
该图显示需要查找 ZLoad 和 Z2。
图 6. 该图显示需要查找 Z Load 和 Z 2。
由于观察线路的输入阻抗每半波长重复,因此我们可以推断出 0.574λ 线路等效于 0.074λ 线路。考虑到这一点并使用上一个示例的结果,我们有 Z Load = 50 × z Load = 100 - j50 Ω 和 Z 2 = 50 × z 2 = 25 - j25 Ω。
朝向发
电机和负载规模的波长
许多教科书以及商业史密斯圆图都包含两种波长标度,一种标为“朝向发生器的波长”,另一种标为“朝向负载的波长”(下图 7)。

示例史密斯圆图显示“朝向发生器的波长”和另一个“朝向负载的波长”标签。
图 7. 示例史密斯圆图显示“朝向发生器的波长”和另一个“朝向负载的波长”标签 [单击图像放大]。
“朝向发生器的波长”刻度按顺时针方向增加,而“朝向负载的波长”刻度按逆时针方向增加。“
发电机”和“负载”术语的使用有时会引起混淆。为了避免这种类型的混乱,请记住,终端的实际功能(即是否是源阻抗)并不重要。当我们将串联传输线添加到终端时,可以通过在史密斯圆图上顺时针旋转找到该线的输入阻抗和反射系数。另一方面,当我们减少线的长度并接近终点时,旋转是逆时针的。
作为阻抗匹配元件的传输线
我们现在可以很好地介绍我们在前面几节中提到的基于传输线的阻抗匹配。例如,假设我们需要将 Z L = 100 + j50 Ω 转换为 50 Ω。负载阻抗 Z L 实际上与我们在上面示例 1 中使用的值相同。图 9 再现了图 2 的史密斯圆图以及一些附加细节。
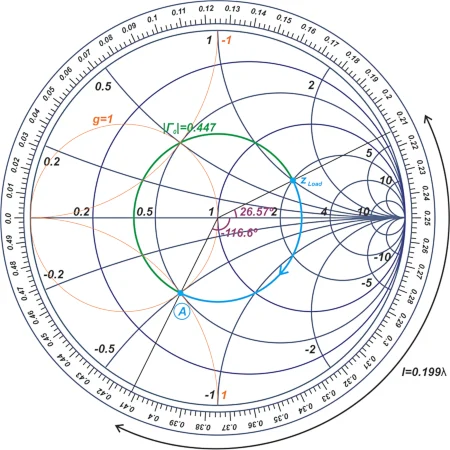
图 2 中的史密斯圆图包含更多详细信息。
图 9. 图 2 中的史密斯圆图以及其他详细信息 [单击图像放大]。
在此示例中,我们特意选择了线路的长度,使我们从负载阻抗 z Load 移动到点 A,该点位于 g = 1 恒定电导圆上。线路的电长度为 71.585°,对应于 0.412λ - 0.213λ = 0.199λ 的长度(根据波长尺度)。
由于我们位于 g = 1 圆上,因此我们可以向线路输入添加一个具有适当电纳的平行组件,并沿着 g = 1 圆移动到史密斯圆图的中心(图 10)。
显示添加并联组件的图表。

图 10. 显示添加并行组件的图表。
从图 9 可以看出,A 点的归一化导纳为 y A = 1 + j。我们需要一个归一化电纳为 -j 的并联元件才能到达史密斯圆图的中心。一种选择是使用并联
电感器。如果感兴趣的频率为 1 GHz,则
电感值如下计算:
\frac{1}{L \omega Y_0}=1 \Rightarrow L=\frac{1}{2 \pi \times 1 \times 10^9 \times 0.02}= 7.96 \text{ } nH
我们可以再次利用传输线的阻抗变换特性,而不是使用集总元件。例如,电长度为 45°(对应于 λ/8 的长度)的短路线可以产生所需的归一化电纳 -j。图 11 对此进行了说明。
密思图显示了 45° 的对应关系,以产生所需的归一化电纳。

图 11. 史密斯圆图显示了产生所需归一化电纳的 45° 对应关系 [点击图像放大]。
上图中,B点对应短路负载。一条 λ / 8 线产生 90° 顺时针旋转,将我们移动到归一化导纳为 -j 的 C 点(根据需要)。终的匹配电路如图 12 所示。
电路图与图 11 史密斯圆图的结果相匹配。

图 12. 与图 11 的史密斯圆图结果匹配的电路图。










