MEMS 加速度计频率响应和带宽规格

　　MEMS 加速度计由几个不同的机械和电气元件组成。这些组件中的每一个都对整体传输函数有贡献，并且可以限制整体系统带宽。
　　在本文中，我们将研究质量-弹簧-阻尼器系统（有时写为质量-阻尼器-弹簧）的频率响应，该系统在 MEMS 加速度计中发挥着关键作用。这使我们能够更好地了解加速度计的整体频率响应和带宽规格。
　　质量-弹簧-阻尼器系统的稳态响应

　　在上一篇文章中，我们将加速度计机械部分的传递函数推导为：

     H(s)=x(s)a(s)=?1s2+bms+k米

　　通常定义以下参数以获得更简单形式的传递函数方程：
　　

ωn=√kmωn=km

Q=mωnb

　　其中 ω n和 Q 分别表示 系统的固有频率和品质因数（也称为 Q 因数） 。

　　使用这些参数，我们可以将传递函数方程重写为：

      H(s)=x(s)a(s)=?1s2+ωnQs+ω2n

　　正如我们使用电路的传递函数来预测其对正弦输入的稳态响应一样，我们可以使用上述传递函数来确定响应于特定频率下的正弦加速度的验证质量位移。例如，如果外部加速度在 f 处呈正弦曲线，则由下式给出：

　a(t)=sin(2π×fin×t)　　

验证质量位移将为：

　　x(t)=|H(2πfin)| sin(2π×fin×t+?)　

  　其中 |H(2πf in )| 和 Φ 分别表示频率 f in处的传递函数的幅度和相位。请注意，这是系统的稳态响应。

　　每当系统状态改变时，系统也会表现出瞬态响应。例如，当我们首先将正弦输入施加到静止的系统或移除正弦加速度时，会观察到系统的瞬态响应。然而，如果我们应用正弦输入足够长的时间，瞬态响应就会消失，我们会观察到系统的稳态响应。
　　传递函数的大小　　让我们检查导出的传递函数，以更深入地了解系统操作。传递函数的大小由下式给出：|H(ω)|= ?1(ω2n?ω2)2+(ωnωQ)2
　　公式 1. 求传递函数的大小

　　当 ω n  = 2π x 500 Hz 和四个不同的 Q 值（0.5、1、1.5、5）时，我们得到如图 1 所示的曲线。

　　图 1. 磁力与频率图
　　图1。

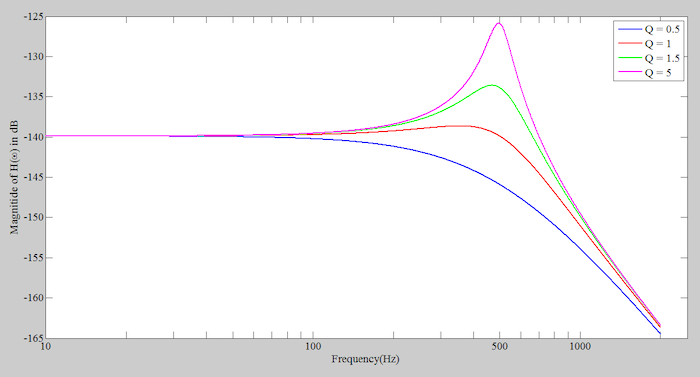
　　正如您所看到的，在非常低的频率下，传递函数的幅度几乎是恒定的。方程 1 给出了 |H(ω)| 的值 直流（或低频）加速度为：　

　|　|H(f=0)|=1ωn　

　当我们接近系统固有频率 f = 500 Hz 时，传递函数的幅度会根据 Q 因子值而增加或减少。高于固有频率，响应幅度会减小，并且我们有一个类似于低通电路的滚降区域。典型 MEMS 加速度计中采用的质量-弹簧-阻尼系统在谐振频率附近呈现增益峰值，类似于图 1 中的粉色曲线。

　　剩下的问题是，我们可以在什么频率范围内使用该系统来测量加速度？
　　需要平坦的响应
　　为了能够准确测量加速度，我们需要平坦的响应。为了更好地理解这一点，假设外部加速度可以写为 f in1 和 f in2处的两个正弦项之和，如下所示：

　atotal(t)=sin(2π×fin1×t)+sin(2π×fin2×t)　

　假设系统引起的相移可以忽略不计，我们有：

　

xtotal(t)=|H(2πfin1)|sin(2π×fin1×t)+|H(2πfin2)|sin(2π×fin2×t)

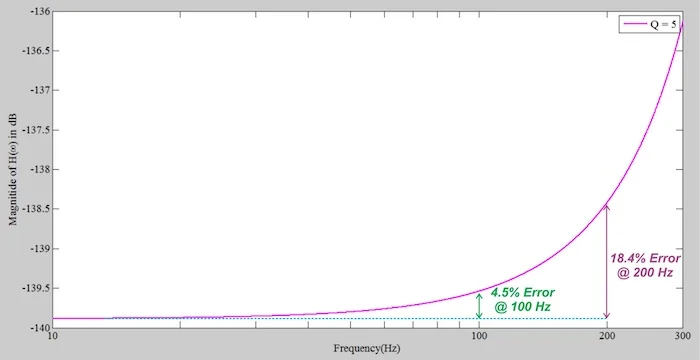
　　仅当系统响应对于所有感兴趣的频率分量都是恒定的时，总位移才与所施加的加速度成正比，即 |H(2πf in1 )| = |H(2πf in2 )|。因此，我们需要平坦的频率响应。

　　实际上，即使在非常低的频率下，响应幅度也不是恒定的。图 2 显示了 ω n  = 2π x 500 Hz 和 Q = 5情况下的传递函数曲线的放大版本。

　　图 2. 传递函数曲线的放大版本
　　图 2.
　　您可以验证 |H(f)| 100 Hz 时比 |H(f)| 高 4.5% 在直流（或低频）加速度下。另外，|H(f)| 200 Hz 时比其 DC 值高 18.4%。
　　上述讨论强调了加速度计的一个重要规格：加速度计带宽。
　　加速度计带宽规格
　　加速度计的带宽被指定为响应幅度相对于幅度响应的直流（或低频）值保持在特定允许偏差内的频率范围。
　　我们假设图 2 中的曲线是加速度计的整体响应（而不仅仅是质量-弹簧-阻尼器系统的响应）。利用图 2 所示的传递函数，系统可以考虑使用 100 Hz 的有效带宽，以将响应误差保持在 4.5% 以下。这种有效带宽概念可能与用于放大器和滤波器等电子组件的带宽定义有些不同。让我们看看商业加速度计的带宽是如何定义的。

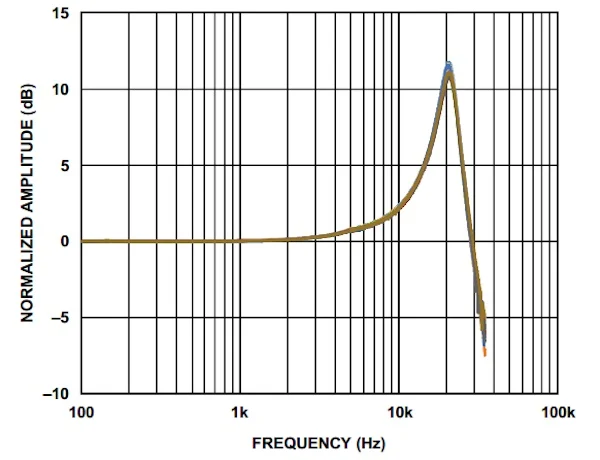
　　以下ADXL1001数据表摘录显示，加速度计的 5% 带宽为 4.7 kHz。

　　表 1. ADXL1001 的频率响应信息由Analog Devices提供。
　　频率响应
　　传感器谐振频率  21kHz
　　5% 带宽  4.7kHz
　　3分贝带宽  11kHz
　　请注意，还给出了基于 3 dB 概念的第二个带宽规范。这为我们提供了幅度响应与响应的 DC（或低频）值相比变化 3 dB 的频率。
　　正如您所看到的，响应偏差（即响应幅度的增加）源自传感器谐振频率处的增益峰值。
　　信号调理电路的频率响应
　　在上面的讨论中，我们只考虑了质量-弹簧-阻尼器系统的频率响应。
　　质量-弹簧-阻尼器系统的输出信号通常由内部放大器、同步解调器以及的低通滤波器进一步处理。对于某些加速度计（例如 ADXL1001），这些电气元件的带宽超出了质量-弹簧-阻尼器系统的谐振频率，因此，我们观察到加速度计频率响应中谐振频率附近的增益峰值。然而，一般来说，加速度计的内部低通滤波器的截止频率可能低于传感器的谐振频率，并限制了系统的整体带宽。
　　在下一篇文章中，我们将讨论低通滤波器如何限制带宽并化加速度计的分辨率和动态范围。