让我们开始反转上一期检查的两级限制器图中个电池的极性,我们在图 1 中再次提出。从已经执行的定性分析,很容易推断出如果 V 01 = ? V 02,输出信号的趋势如图2所示,类似于方波。
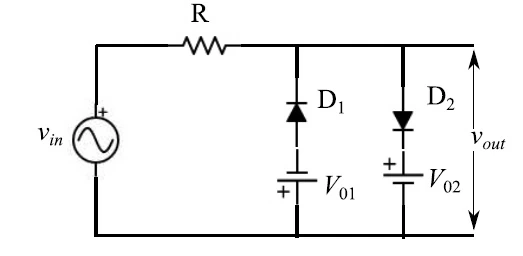
图 1:个电池极性相反的两级限制器电路

这种仓促的分析源于两个二极管的理想条件。在真实条件下。需要齐纳二极管的电压-电流特性的解析表达式。为此,我们观察到,与传统二极管相比,齐纳二极管具有更加非典型的行为:除了必须在反向偏压下工作之外,其两端的电压必须达到击穿值 (V z )的量级,其行为几乎是渐近的(图 3)。在这些工作条件下,即使电流剧烈变化,电压也能保持稳定。然而,为了实现稳压器,齐纳二极管必须进行适当的配置,因为任何电流变化都是由相应的电压变化引起的,就像上一期已经研究过的情况一样。
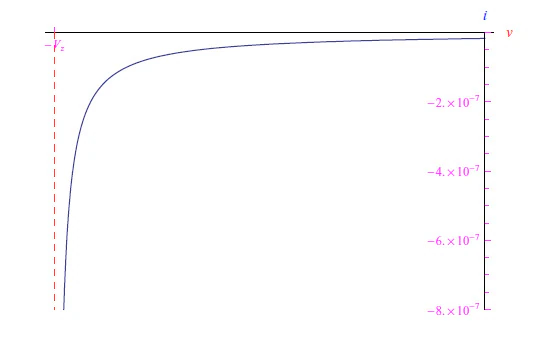
经过繁琐而费力的数学分析,我们证明不可能同时应用这两个条件,为此我们仅选择渐近分支(对于 v = ?V z ),然后将其扩展到 v = 0。这里我们有正如我们从图 3 中的图表中看到的,正是由于这种近似,非零电流值。但这不应该让我们担心,因为无论如何工作点都位于 v = ?V z的右邻域内。(回想一下我们对符号的约定:大写字母表示与时间无关的量,反之亦然;除了我们普遍采用小写的电流)。电压-电流特性的解析表达式如下:

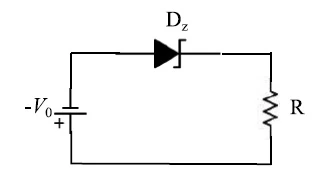
我们使用的测试电路如图4所示,其中电阻R的值以及V 0都是自由参数。
二极管两端的电流和压降进行了无量纲化和标准化。通过无量纲变量的电流:

否则,电路简单地解决:

在情况 (2) 中,无量纲电压-电流特性由下式给出:
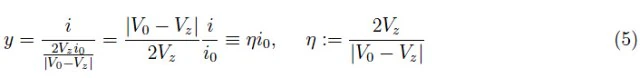
通过应用基尔霍夫第二原理,我们有:
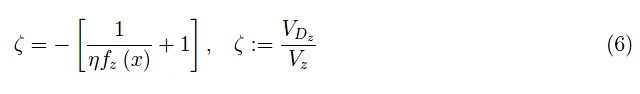
免责声明: 凡注明来源本网的所有作品,均为本网合法拥有版权或有权使用的作品,欢迎转载,注明出处。非本网作品均来自互联网,转载目的在于传递更多信息,并不代表本网赞同其观点和对其真实性负责。