晶体的负载电容:一个关键因素
许多石英晶体振荡器,例如 Pierce、Colpitts 和 Clapp 型拓扑,都在其感性区域(图 1所示的电抗曲线中的f s和 f a之间)操作晶体。
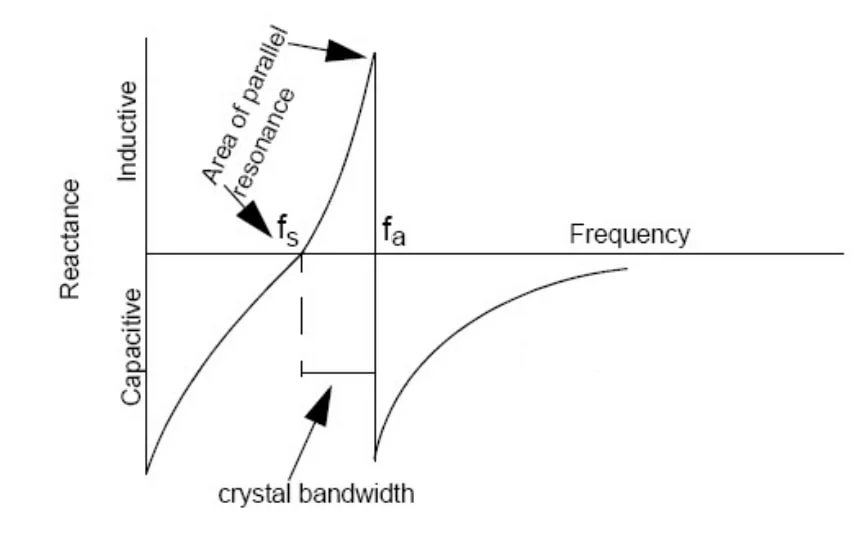
图 1.图片由Cypress提供。
对于这些振荡器,从晶体端子“看到”的总电容至关重要。由振荡器电路产生的电容通常称为晶体的负载电容。这个负载电容如何影响我们的设计?由于晶体在 f s和 f a之间工作,因此它实际上充当电感器。该有效电感与负载电容一起形成一个 LC 谐振回路,决定振荡频率。如果负载电容为 C L并且晶体以 f L振荡,则负载电容的电抗为:

晶体将以表现出电抗

的频率振荡。
因此,给定的负载电容限制晶体在 f s和 f a之间的特定点振荡。如果改变负载电容,就会得到不同的振荡频率。这就是为什么晶体制造商给出了特定负载电容下的晶体频率。
匹配负载电容
图 2 显示了将晶体连接到微控制器的常见布置。

图 2.
这里,C Pin +C Stray对 MCU 引脚的电容以及连接到晶体端子的 PCB 走线的杂散电容进行建模。C引脚+C杂散通常在 2 pF 至 5 pF 范围内。较短的 PCB 走线可以减少杂散电容。
我们还添加了 C L1和 C L2,以将电路板的负载电容与晶体制造商指定的负载电容相匹配。这两个
电容器通过地串联连接。因此,电路的有效负载电容为:

该总负载电容应与晶体制造商指定的值相匹配。如果我们的电路对晶体提供不同的负载电容,则它不会在指定的标称频率下振荡。它将被“拉”到稍微不同的频率。
剩下的问题是,当我们改变负载电容时,给定晶体的频率会被拉多远?
为了回答这个问题,我们首先需要推导出一个方程,给出任意负载电容的振荡频率。
任意负载下的振荡频率
假设晶体连接到任意负载电容 C L,如图 3 所示。
晶体会以什么频率振荡?

图 3.
忽略晶体电阻 R m,谐振发生在上述网络的总导纳为零的频率处:
j C L ω L + j C 0 ω L + 1 j L米ω L + 1 j C米ω L= 0
其中 ω L = 2πf L和 f L表示 C L处的振荡频率。使用一些代数,我们得出以下方程:
f L = 1 2 π √ L m C m× √ 1 + C m C L + C 0
等式 1。
可以看出,晶体的串联谐振频率 (f s )由下式给出:
f s = 1 2 π √ L m C m
因此,公式 1 简化为:
f L = f s √ 1 + C m C L + C 0
由于 C m C 0 + C L,我们可以使用泰勒定理将该方程近似为:
f L = f s ( 1 + C m 2 ( C L + C 0 ))
等式2。
这是一个重要的方程,显示了晶体振荡频率如何随负载电容变化。
拉动曲线
当我们电路的负载电容与标称值不匹配时,晶体将被拉动以稍微不同的频率振荡。我们需要知道当我们改变负载电容时,给定晶体的频率会被拉动多远。
为了描述这一点,我们可以将方程 2 重新排列为:
Δ f f s= f L ? f s f s= C m 2 ( C L + C 0 )
为了以 ppm 表示频率变化,我们只需将结果乘以 10 6即可得到:
Δ f f s= f L ? f s f s= C m 2 ( C L + C 0 )× 10 6 ( in ppm )
等式 3。
该方程的图形表示有时称为晶体的牵引曲线。例如,当C m =20 fF,C 0 =4.5 pF时,我们得到以下牵引曲线。

图 4.图片由Ecsxtal提供。
该曲线显示晶体频率如何随负载电容变化。例如,对于上述晶体,当采用45pF的负载电容时,振荡频率比fs高约+200ppm。
在某些应用中,我们需要通过改变负载电容来改变晶体频率。在这些应用中,我们需要能够提供更高“拉伸性”的晶体。拉伸曲线使我们能够评估晶体的拉伸能力。在图 4 所示的示例中,我们观察到,随着负载电容从 100 pF 变为 10 pF,晶体频率相对于 f s从 +100 ppm 变为 +700 ppm。
微调振荡频率
我们看到设计的引脚和杂散电容会影响负载电容并影响振荡频率。此外,连接到晶体端子(图 2 中的 C L1和 C L2 )的电容器具有有限的容差。
我们需要考虑这些变化来调整振荡频率。在这些情况下,我们可以使用额外的串联和并联电容器来修改负载电容并将晶体拉回其所需的工作频率。

图 5 显示了示例原理图。
图 5.图片由Maxim Integrated提供。
这里,C evkit表示 IC 引脚电容以及 PCB 走线的杂散电容。C 14和C 15是串联牵引电容器,而C 16是并联牵引电容器。串联电容器会提高振荡频率,并联电容器会减慢振荡频率。
一些 IC 采用内部电容器阵列,允许用户微调负载电容并满足应用的频率容差要求。图 6 说明了NXP 的 ZigBee 平台MC13224中采用的这项技术。

图 6.图片由 NXP 提供。
根据器件数据表,振荡频率可以调整为目标频率整体条件的±30 ppm。片上负载电容器还可以节省电路板面积。请注意,图 5 和 6 中所示的拓扑假设晶体可以提供所需的可拉性。
微调灵敏度
从图 4 中可以看出,随着负载电容的增加,牵引曲线的斜率减小。这表明,负载电容较高时,频率对元件容差的敏感度会降低。
为了表征这一点,我们可以采用拉力方程(方程 3)相对于 C L的一阶导数。这给我们提供了以下方程,通常称为调整灵敏度:
T S = ? C m 2 ( CL + C 0 ) 2 _× 10 6 ( ppm / p F ) _ _
例如,当 C m =20 fF、C 0 =4.5 pF 时,我们得到如图 7 所示的调整灵敏度曲线。

图 7.
上图显示,在负载电容较低时,电路对负载电容值表现出较高的灵敏度。在某些设计中,例如可穿戴应用,我们可能希望使用负载电容较低的晶体来降低功耗并加速振荡器启动;然而,上面的曲线表明,这可以增加振荡器对电路杂散电容的灵敏度。
可以使用调整灵敏度规格来评估负载电容变化引起的频率变化。然而,应该注意的是,给定的调整灵敏度值仅在规定负载电容的几皮法范围内有效。
例如,上图显示,C L = 40 pF时,调整灵敏度为 -5 ppm/pF 。此调整灵敏度仅在 C L =40 pF左右有效。如果负载电容变化很小,我们可以将负载电容的变化乘以微调灵敏度值来获得频率变化。例如,如果负载电容从 40 pF 增加到 41 pF,我们预计频率将变化约 -5 ppm。然而,如果负载电容变化几个皮法,我们就不能使用微调灵敏度值来找出频率变化。









