很久以前,在一个遥远的星系(实际上,同一个星系,但银河系正在移动,因此从逻辑上讲,它必须远离当时的位置),我为直流耦合
放大器绘制了一个简单的电路,我认为(在我年轻的天真中)看起来很酷。参见图 1。
图 1这是一个比放大器更好的(温度传感)振荡器。
晶体管偏置经过专门选择:300 o K时 d(Von – Vsat)/dT = 1/300。
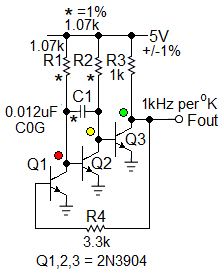
它由三个直接耦合共发射极放大器(Q1 至 Q3)组成,级联增益约为 120 dB (β 3 ),并具有从 Q3 到 Q1 的反向反馈。电容器 C1 旨在提供单个主环路带宽限制、稳定性促进极点。
我迫不及待地想把它连接起来,看看它是如何工作的。剧透警告:它(非常)没有——至少不是作为放大器。
说它“持续振荡”(非常)是轻描淡写的。事实上,“振荡抑制”C1看似可以无限制地增大,而振荡幅度却不会减少一丝一毫。振荡频率降低(与 C1 成反比),但振荡幅度仍然顽固地保持不变。图 2显示了原因。
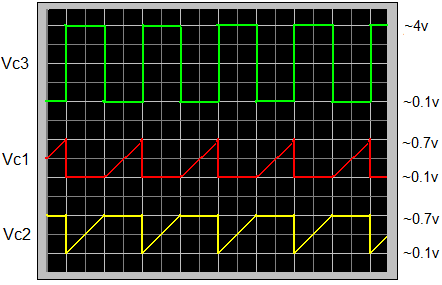
图 2 C1 通过旁路 Q2 提供引发振荡的正反馈,如 Q1 和 Q2 集电极波形所示。
Q1 和 Q2 集电极之间的 C1 连接有效地旁路了 Q2 及其信号反转级,使 Q1 和 Q3 周围的环路反馈的净极性为正,而不是我初预期的负。因此,C1 保证振荡,而不是阻止振荡!
每个振荡周期的 4 步顺序如下:
Vc3:振荡周期从 Q3 关闭开始,(绿色迹线)将 Q3 的集电极 Vc3 驱动至约 4V。
Vc1:这会打开 Q1,将其集电极从 Von = 700 mV 驱动到 Vsat = 100 mV(红色迹线),从而关闭 Q2。
Vc2:同时,C1 将 Vc1 处的 Von – Vsat = 600 mV 转换耦合到 Vc2(黄色迹线),从而保持 Q3 关闭。这种状态一直持续到 Vc2 斜坡回升至 Q3 Von,从而将 Vc3 驱动为低电平(绿色迹线)。
这将关闭 Q1,从而允许 Vc1(红色迹线)将 C1 的左侧斜坡上升至 Von。这将打开 Q2,将 Vc2 驱动至 Vsat(黄色迹线),关闭 Q3,将 Vc3 返回至 4 V(绿色迹线),在步骤 1 开始下一个振荡周期。
这里特别值得注意的是,振荡周期等于 Vc1 斜坡周期 (T1) 和 Vc2 斜坡周期 (T2) 之和,并且振荡频率等于该和的倒数。
T1 = T2 = T
T = R1C1(Von – Vsat)/(5 – (Von + Vsat)/2) + Td(晶体管延迟时间)
Fout = 1/(2T + 2Td)
对 2N3904 数据表的研究表明,Vsat = 100 mV,与温度和集电极电流无关( Ic = ~10 mA),而 Von 随温度和电流以可预测的速率变化。如果仔细选择偏置电流,则可以在有用的温度范围内实现非常接近 Fout = 1000Tabs = (1 kHz/ o K)的温度响应。图 1 中所示的组件值从 270 o K 到 330 o K = -3 o C 到 +57 o C = 27 o F 到 135 o F,这在图 3中绘制为实现的响应(红色曲线)与理想的 1 kHz/ o K(蓝线)相比。
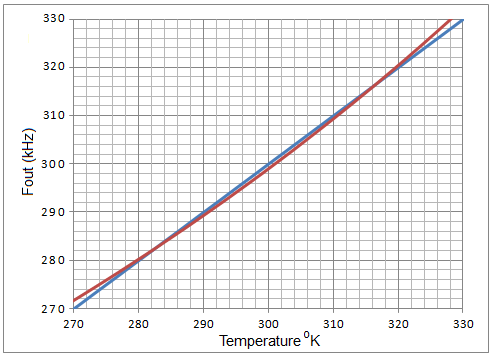
图 3图 1 的输出频率与温度的关系(选项卡)。Fout = 1 kHz(制表符 +/-2 o K)。
因此,图 1 不是放大器,而是有趣的数字温度
传感器的基础。
以下是一些结论性意见。
自加热:所有有源温度传感器都关心的是自加热误差。TO-92 中的 2N3904在静止空气中将自身加热约 200 o C/Watt = 0.2 o K/mW(坏情况,在移动空气中加热较少)。Q3 的功耗 < 2 mW,而 Q2 在周期的一小部分内导通,其散热和温升可以忽略不计。
Q3 贡献了一半的振荡周期,因此图 1 电路的总自热误差为 1 kHz*0.2/2 = ~100 Hz = 0.1 o K。这在大多数应用中是可以接受的(但请注意,Q2 和Q3 应与
电阻器消耗的约 65 mW 良好隔离。
成本/性能:将分立元件电路的价格和性能与竞争 IC 进行比较,对于多部件器件来说,很少会表现得很好,但图 1 的表现并不算太差。其精度(在有用的温度范围内+/- o 2)和分辨率(例如,1/4秒计数间隔约为16位)与典型的数字温度测量芯片(例如,TMP125)相比,其组件的成本也是如此(~2 美元)。


