电气噪音就像税收一样,始终伴随着我们。大多数时候噪声很小,我们可以忽略它,但有一些测量情况必须处理噪声。如何才能限度地减少噪声对测量精度的影响?本文将讨论噪声以及如何限度地减少其对示波器和数字化仪测量的影响。
噪声基本上是除了您要测量的信号之外的一切。它可以包括随机电信号、电力线信号等周期信号或串扰拾取的干扰信号。我们将处理随机噪声,这是常见的噪声现象。随机噪声是
电子产品中普遍存在的一种现象。可以使用示波器或数字化仪对其进行测量和分析,图 1中显示了一个示例。
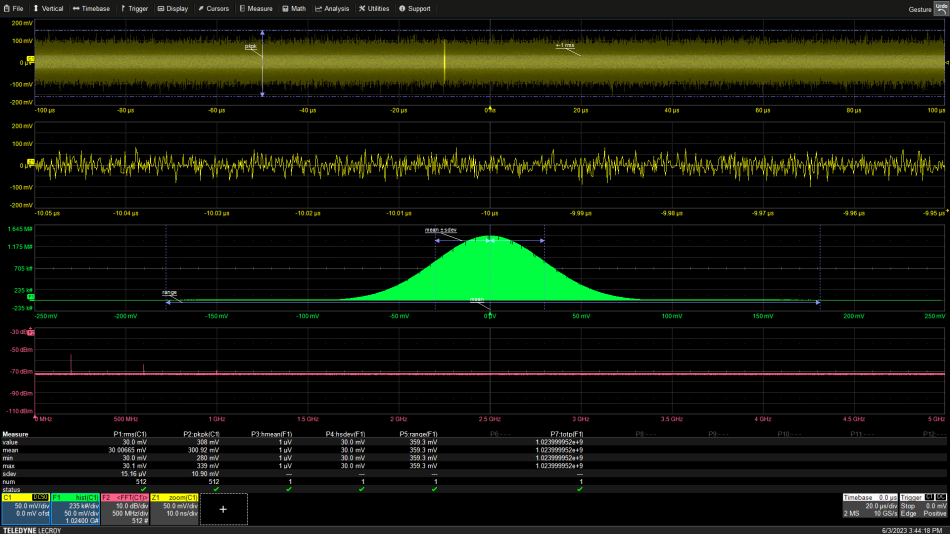
顶部迹线是噪声信号的电压与时间的时域视图。该迹线下方是所采集信号的水平扩展缩放视图。噪声是一系列随机电压值。测量参数读取参数 P1 中采集的噪声迹线的均方根值和 P2 中的峰峰值。
从顶部算起的第三条迹线是信号的直方图。该直方图绘制了称为仓的窄电压范围内测量的电压值的数量作为仓标称电压的函数。该直方图是噪声值概率分布的近似值。这是噪声信号的统计视图。被测量的噪声具有高斯或正态概率分布及其特征的钟形分布。参数P3记录接近于零的直方图平均值。参数P3是直方图标准差。标准差是概率密度关于平均值的分布的度量。对于均值为零的信号,标准偏差等于参数 P2 中读取的均方根值。P5是直方图范围,差值,和填充垃圾箱限制。高斯噪声是无界的,这意味着峰峰值和直方图范围值都会随着测量总数的增加而增加。如果您任一参数,您还应该包括测量次数以获得完整的描述。
底部轨迹是噪声信号的快速傅立叶变换 (FFT)。FFT 就像频谱分析仪一样,显示信号随频率的分布。噪声频谱平坦,在整个频谱范围内功率相等。这种类型的噪声被称为“白”噪声。
电气测量中还遇到许多其他噪声分布。图 2显示了常见的四种不同分布的子样本。
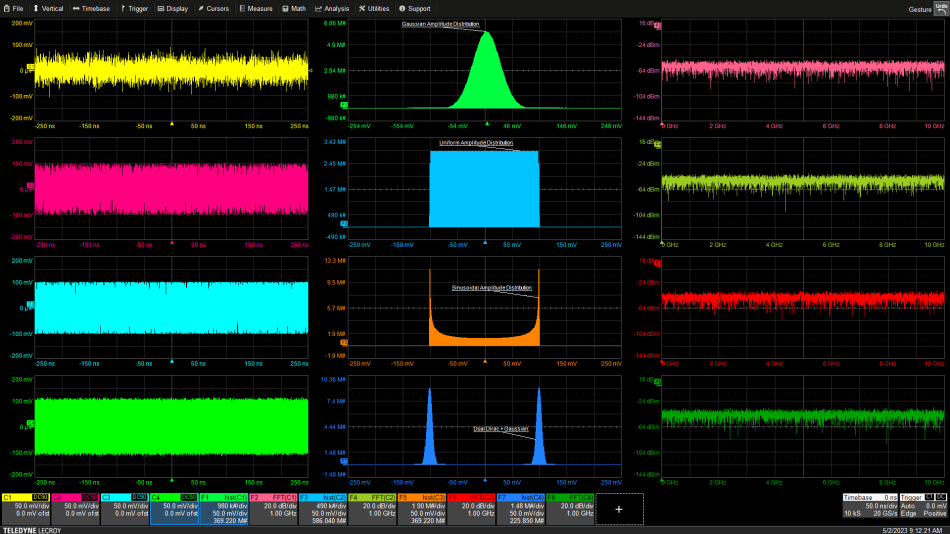
图 2四种不同随机噪声分布的示例:高斯分布、均匀分布、正弦分布和双狄拉克分布。每个视图都是(从左到右)时域、直方图和频域。资料·皮尼
左栏中的时域视图都很相似,因为它们显示随机样本值。直方图显示了的差异。我们在顶行看到前面提到的高斯分布的钟形分布。从上往下数第二行是均匀分布的视图。顾名思义,均匀分布的样本计数均匀分布在所有可能的幅度箱值中。这反映在直方图中,该直方图显示每个幅度值的数量相等。量化噪声是均匀分布的一个例子。
从上往下数第三行显示了正弦分布噪声的三个域视图。正弦分布在正弦波峰值附近具有大量样本值,且变化率较慢。零交叉附近的样本较少,其中变化率,导致鞍形。
底行显示对偶狄拉克分布的统计域视图。这种分布常见于测量时间抖动。该分布显示两个不同的峰值,代表两个可能的振幅质心。
所有分布都具有平坦的频谱,并且在整个频率跨度上能量分布相等。这一观察结果很有帮助,因为可以通过使用
滤波器限制噪声的带宽来降低噪声幅度。滤波器的频率响应应以很小的衰减通过所需信号的频率,同时应衰减信号频谱之外的噪声。
降低噪音
有两种降低噪音的基本方法。种是使用平均法。大多数示波器提供两种常见的平均类型:整体平均和 Boxcar 平均。正如我们所看到的,噪声由具有随机幅度和极性的电压样本组成。整体平均采集多个波形记录,并在所有采集中对每次采集的第 n 个样本进行平均,将噪声平均到其平均值,从而提高了信噪比,如图 3所示。

图 3整体平均值采用每次采集的第 n个样本(如光标下的样本)并将它们相加。将该总和除以平均值数 (N),以获得迹线的平均值。资料·皮尼
该图显示了 16 次采集,其中添加了每次采集中的相同样本,然后通过采集次数进行归一化以获得该样本点的平均值。请注意,图中部的平均波形比单个采集的波形更平滑。整体平均的主要缺点是它需要多次采集。
Boxcar 平均是一种可应用于单次采集的方法。它由 n 个相邻样本的平均值组成。平均样本数决定了信噪比的改善。图 4提供了如何计算 Boxcar 平均值的示例。

图4求光标标记样本点附近7个样本的平均值。资料·皮尼
Boxcar 平均是与所选样本相邻的固定数量样本的运行平均值。垂直光标标记第 n 个样本。设置蓝色测量门将平均值的测量限制在以光标为中心的 7 个样本的范围内。这 7 个样本的平均值 P4 是 F6 缩放的轨迹注释框中显示的该点的 Boxcar 平均值。对 Boxcar 平均值中的每个样本重复此操作。幸运的是,Boxcar 数学函数自动完成所有这些工作,生成如图所示的底部波形。
降低噪声的第二种方法是降低信号采集的带宽。该技术利用选择的滤波器来传递所需信号,但尽可能多地衰减噪声频谱。

图 5提供了使用整体平均、Boxcar 平均和带通滤波的这些方法的示例。
图 5比较整体平均、Boxcar 平均和滤波对信噪比的影响。资料·皮尼
顶部迹线是采集的 10MHz 正弦波形,用作参考。左栏是采集的波形。中心列是采集波形的水平扩展或缩放。噪
声表现为正弦波上的参差不齐的区域。右边的列是采集波形的 FFT。正弦波在 10 MHz 处显示为垂直谱线。噪声在 FFT 的整个跨度上以 -65dB 的水平进行频谱水平扩展。
该总体平均值取自 256 次收购。变焦轨迹非常平滑,几乎没有明显的噪点。FFT 在 10 MHz 处具有相同的垂直谱线。通过平均过程,基线所示的噪声水平已降低了 20 dB 以上。原始采集的基线约为 -65 dB,基线已降至 -85 dB 以下。
上数第三行显示了 Boxcar 平均 7 个样本的效果。查看中心列中的缩放轨迹,噪声的影响有所降低,但不如对更多样本进行平均的整体平均减少那么多。FFT 显示基线降低并伴有扇形成形。Boxcar 平均将 n 个样本以相等的权重相加,可以被认为是一个简单的数字滤波器。扇形形状是该滤波器的频率响应。显然,噪声的衰减不如前面的示例,因为平均的样本较少。可以通过增加平均样本数来提高信噪比,这会降低有效带宽。这件事一定要认真做,
底行显示了对采集信号应用窄带通滤波器的效果。滤波器的带宽为 500 kHz,以 10 Mhz 为中心,可衰减该带宽之外的噪声。FFT 显示噪声得到了很好的降低,但滤波器中心频率附近的衰减要小得多。与 Boxcar 平均一样,滤波可以应用于单次采集。
这在实际测量中效果如何? 图 6比较了 40 kHz 超声波测距仪的降噪结果。

图 6比较 40 kHz
超声波测距仪上的平均、Boxcar 平均和带通滤波的降噪技术。资料·皮尼
顶部迹线是原始波形,传输脉冲发生在采集后 1 毫秒。3.35 ms 处的回波略高于噪声水平。所有三种技术都提高了信噪比,并且回声在本底噪声之上清晰可见。简单的视觉比较表明带通滤波器提供了的信噪比增强。平均和 Boxcar 平均性能可以通过分别增加采集数量或样本数量来提高。
对信号应用带通滤波器的结果是什么?让我们比较原始采集的结果和使用带通滤波器的结果。图 7比较了两个波形。

图 7使用门控 x@max 参数比较原始采集和带通滤波采集的结果,以计算回声的延迟时间。资料·皮尼
使用 x@max 参数计算发射脉冲和回波之间的延迟,该参数测量波形值处的时间。x@max 参数经过时间选通以隔离发射脉冲和回波脉冲。参数数学计算每个处理波形的时间差。P3 显示原始采集的时间延迟,P9 是带通滤波采集的时间延迟。蓝色参数标记显示 x@max 位置。原始波形的延迟测量范围(值和值之间的差)为 2.45 ms。带通滤波波形的范围是 50.5 ms。假设室温下声速为 344.44 m/s,则使用平均延迟测??量的标称距离约为 0.79 m。距离测量的不确定度为0。原始波形为845 m(基本无法使用)。带通滤波波形的距离不确定度为 0.0174 m(约 0.7 英寸)。显然,降噪是一个有用的工具。
这些降噪技术对于确保准确测量非常有用。请记住,如果仪器的信号输入利用设备的整个动态范围,它们的工作效果。即使在应用降噪技术之前,这也可以化信噪比。






