当我们使用模数 (A/D)
转换器对模拟信号进行数字化时,转换器的输出通常包含一些小的 DC 偏差:即数字化时间样本的平均值不为零。该 DC 偏差可能来自原始信号模拟信号或 A/D 转换器内的缺陷。
数字信号处理中直流偏置污染的另一个来源是当我们将离散序列从 B 位表示截断为小于 B 位的字宽时。无论来源如何,信号上不需要的直流偏置都会导致问题。
当我们执行频谱分析时,信号上的任何 DC 偏置都会在频域中显示为零 Hz 处的能量,即 X(0) 频谱样本。对于 N 点快速傅立叶变换(FFT),X(0) 频谱值与 N 成正比,对于大型 FFT 而言,N 会变得非常大。
当我们绘制频谱幅度时,绘图软件将适应任何大的 X(0) 值,并压缩我们更感兴趣的频谱的其余部分。
音频信号中的非零直流偏置电平特别麻烦,因为连接两个音频信号或在两个音频信号之间切换会导致令人不愉快的咔嗒声。在现代数字
通信系统中,正交信号上的直流偏置会降低系统性能并增加误码率。
话虽如此,很明显,许多 DSP 从业者对 DC 去除方法很感兴趣。
块数据 DC 去除
如果您进行非实时处理,并且信号数据是在块长度为 N 的块(固定长度序列)中采集的,则 DC 去除非常简单。我们只需计算 N 个时间样本的平均值,然后从每个原始样本中减去该平均值即可产生一个新的时间序列,其 DC 偏置将非常小。
该方案虽然非常有效,但与连续吞吐量(实时)系统不兼容。对于实时系统,我们强制使用
滤波器来去除直流。
实时 DC 去除
作者遇到了三种建议的 DC 去除滤波器,如下图 13-62(a)、(b)和(c)所示。忽略这些去直流滤波器的恒定增益,所有三个滤波器都具有与图 13-62(d)中的一般去直流滤波器结构相同的性能,其 z 域传递函数为

图 13-62(c) 和 (d) 中的滤波器是否等效并不明显。您可以通过编写与图 13-62(c) 滤波器的反馈路径中的各个节点相关的时域差分方程来验证该等价性。接下来,将这些方程转换为 z 变换表达式,并求解 Y(z)/X(z) 以生成yieldEq。(13-118)) 如上所述。
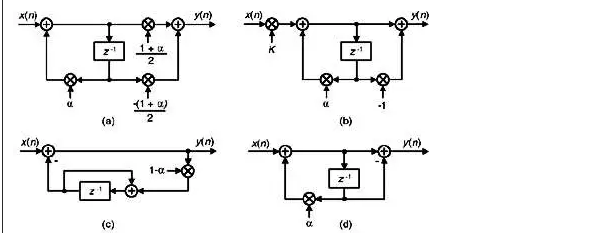
图13”62. 用于消除直流偏置的滤波器。
由于去直流滤波器可以使用图 13-62(d) 中的通用去直流滤波器进行建模,因此我们在图 13-63(a) 和(b)中提供了 α = 0.95 时通用滤波器的频率幅度和相位响应下面。
滤波器的极点/零位置如图 13-63(c) 所示,其中零位于 z = 1 处,在 DC(零 Hz)处提供无限衰减,而极点位于 z = α 处,使得 DC 处的幅度陷波非常尖锐。a 越接近 1,以 0 Hz 为中心的频率幅度陷波越窄。图13-63(d)显示了通用滤波器的单位样本脉冲响应。
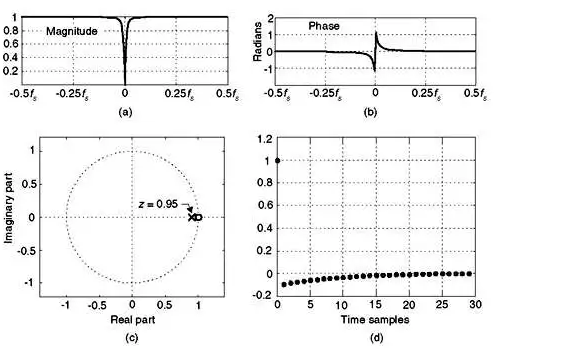
图13-63。除直流滤波器,α = 0.95:(a) 幅度响应;(b) 相位响应;(c) 极/零位置;(d) 脉冲响应。
下图 13-64 显示了一般去直流滤波器(α = 0.95)的时域输入/输出性能,当其输入是正弦曲线时,从第 100 个采样点开始,突然受到 2 的直流偏置污染,并在第 200 个采样点消失。 。去直流滤波器效果很好。
带量化的实时去直流
由于通用去直流滤波器具有反馈,因此 y(n) 个输出样本可能需要比用于 x(n) 个输入样本的二进制字宽更宽的二进制字宽。这可能会导致定点二进制实现中的溢出。图13-62(a)和(b)中的(1+α)/2和K的缩放因子小于1,以化y(n)二进制溢出的机会。
在定点硬件中,y(n) 样本通常被截断为与输入 x(n) 相同的字宽。这种量化(通过截断)将在量化的输出样本上引入负直流偏置,从而降低我们所需的直流去除效果。
当我们截断二进制样本值时,通过丢弃一些有效位,我们会在截断的样本中引入负误差。
幸运的是,我们可以将该误差值添加到下一个未量化信号样本中,从而增加其正直流偏置。当下一个样本被截断时,我们添加的正误差将化由下一个样本截断引起的负误差。
下面的图 13-65(a) 显示了在图 13-62(c) 中给出的去直流滤波器的反馈路径中添加了一个量化 Σ-Δ
调制器。截断量化(Q 块)引起的正误差被延迟一个采样时间并反馈到量化器输入。
由于调制器具有噪声整形特性,其中量化误差噪声的频率上移,远离零 Hz(DC),因此滤波器输出端的总体 DC 偏置被化。等效量化噪声整形过程可应用于图 13-62(d) 通用去直流滤波器的直接形式 I 版本,如图 13-65(b) 所示。
同样,正量化误差被延迟一个采样时间并添加到量化器输入中。重申一下,图 13-65 中的去直流滤波器用于通过量化来避免二进制数据溢出,而不使用缩放乘法器。


