交替信号与恒定值信号的加法/减法
添加信号:正向钳位
让我们从正弦信号开始,如图 1 中的红色曲线所示。
现在,我们向其添加一个幅度为 1.5 的恒定值信号。我们的输出信号变为y(t) = x(t) + 1.5。获得的图由同一图中的蓝色曲线显示。
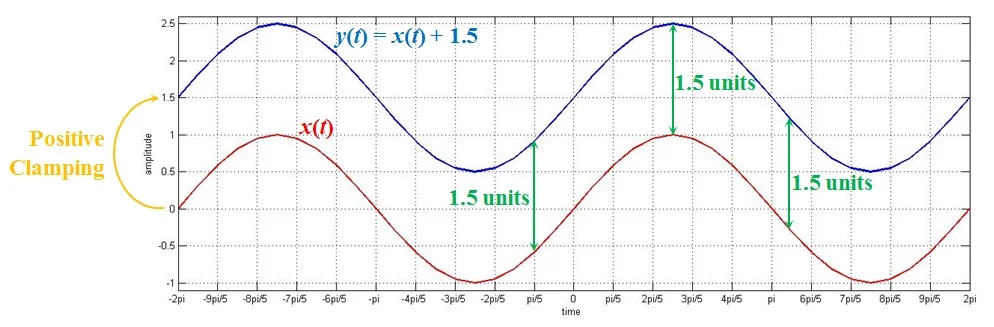
图 1. 交变信号与幅度为 1.5 的恒定值信号相加
正如您所看到的, y(t) 与 x(t) 相同,但沿其迹线移动了 1.5 的幅度(添加到其中的常数值)。
这很好地演示了当我们将恒定值信号添加到交替信号中时会发生什么 - 后者被转移到前者的水平。交流信号参考电平的这种变化称为“钳位”。由于在本例中存在向正值的转变,因此我们可以将其称为“正钳位”。
如果我们将交替信号与常值信号相加,会发生什么?该数学方程为y(t) = 1.5 + x(t)。
然而,结果是一样的。为什么?与简单数学一样,加法是可交换的,这意味着 x(t) + 1.5 = 1.5 + x(t)。
减去信号:负钳位
接下来,让我们尝试减法。我们首先从交替信号中减去示例的常值信号。令 y(t) 为 x(t) - 1.5。
与此相对应的输出如图2中的蓝色曲线所示。通过将该曲线与代表原始信号的红色曲线进行比较,我们可以看到信号的幅度总体减少了1.5。
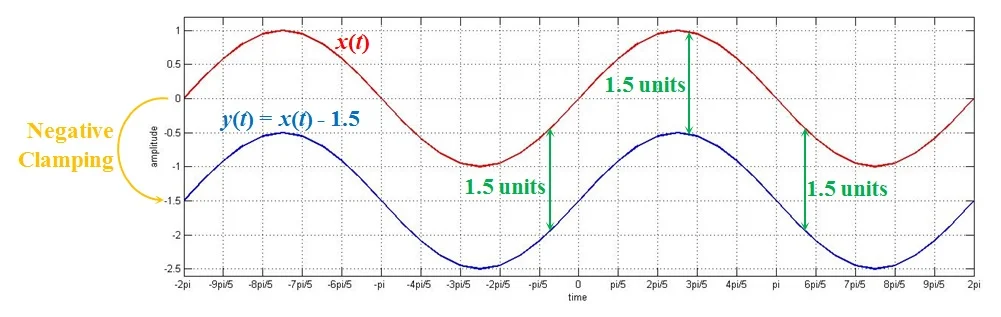
图 2.从交流信号中减去幅度为 1.5 的恒定值信号的效果
从图中可以明显看出,其直接结果是将交流信号钳位至 -1.5。由于钳位是朝着负值,所以我们称之为“负钳位”。
当我们将其写为 y(t) = x(t) - 1.5 为 y(t) = - 1.5 + x(t) 时,我们可以看到,即使在这种情况下,也必须发生钳位,但朝向负值。
作为延续,现在让我们尝试颠倒减法的顺序。也就是说,让我们的输出信号为 y(t) = 1.5 - x(t),而不是 y(t) = x(t) - 1.5。
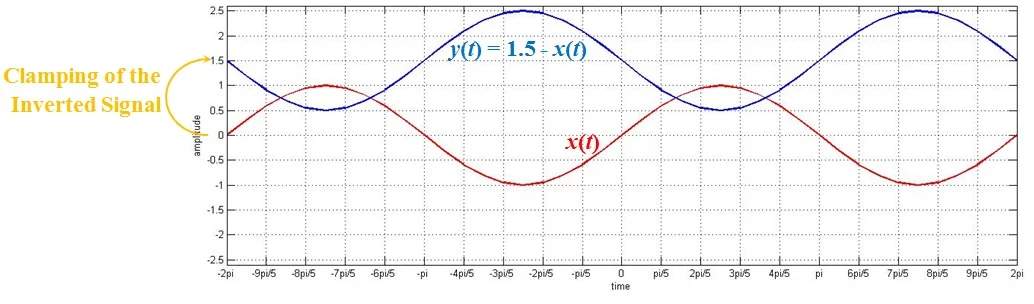
图 3 显示了该操作对应的结果:
图 3.从幅度为 1.5 的恒定值信号中减去交流信号的效果
乍一看,这似乎把我们“钳制”的想法抛到了九霄云外。然而,这并不完全正确。
为什么?
仔细观察。图中的蓝色曲线是交替信号,但沿水平轴反转并钳位在 1.5 电平。
在这种情况下,我们的输出方程是 y(t) = 1.5 - x(t),这与 y(t) = 1.5 + {-x(t)} 相同。这表明,在这里,反转的 x(t) 应被限制在 1.5 的水平。
关于加法或减法的结论
我们可以得出结论,恒定值信号与交替信号的相加或相减总是会导致将交替信号钳位到由常数决定的值。
从
电子学的角度来说,产生钳位的电路称为“钳位器”。
因此我们知道,在信号中执行的加法/减法运算(其中至少一个信号是恒定值)可以在应用钳位器的所有场景中使用。基线稳定器、直流恢复电路以及用于在设备工作范围与输入信号工作范围之间建立兼容性的电路只是您可能会看到这些操作实际应用的几个应用示例。
恒定值信号与交变信号相乘的效果
在本节中,我们将了解恒定值信号与交替信号相乘的效果。具体来说,我们将幅度为 1.5 的常值信号与交变信号x(t) 相乘,该交变信号是周期为 2π 的正弦波(如图 4 中的红色曲线所示)。
结果图如图 4 中的蓝色曲线所示:
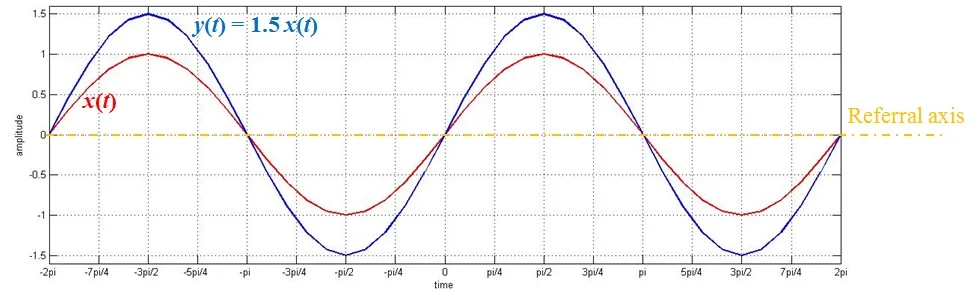
图 4.幅度为 1.5 的常值信号与交流信号相乘
从图中可以看出, x(t) 在 –π/2 处的值为 -1,而 y(t) 的值为 -1.5(即 x(t) 值的 1.5 倍)。类似地,在时刻 0、π/2 和 3π/2,y(t) 的值分别为 0、1.5 和 -1.5。您会注意到,这些值是 x(t)(分别为 0、1 和 -1)乘以 1.5 的值。
这表明,当我们将信号乘以常数值时,我们得到的信号的值乘以相同的因子。
此时,我们应该讨论图 4 中的一个重要点。与加法和减法(如图 1 至图 3 所示)不同,乘法运算不会导致信号钳位。然而,与加法一样,乘法是可交换的,即y(t) = 1.5 x(t) = x(t) 1.5。
关于乘法的结论
从所提出的讨论中可以清楚地看出,与大于 1 的常数相乘的信号会增加其幅度而不对其进行钳位。这本质上是输入信号的放大倍数,该倍数由常数值决定。因此,这种乘法运算在电子
放大器使用的所有情况下都有其用途。
其应用示例包括通信系统中的
低噪声放大器、收音机/电视机的音频/视频放大器以及构成众多电子电路组成部分的
运算放大器。
常值信号的微分和积分
根据数学,常数的微分为零。即使在信号的情况下也是如此。也就是说,通过对常值信号进行微分,我们将得到零值信号。这是许多电子设计中使用的隔直
电容器的工作原理。
另一方面,如果我们对常值信号进行积分,我们会得到一个斜坡,其斜率由常量值决定。恒流斜坡发生器等电路就是根据这一原理工作的。
概括
在本文中,我们分析了对常值信号进行基本信号运算时产生的结果。我们还看到了加法/减法、乘法、微分和积分等运算如何分别产生钳位、放大、直流阻塞和斜坡生成等效果。



