几乎每种形式的数字信息交换都会引入通信错误。有时,这些错误可以被忽略(例如,高分辨率视频中的错误像素根本无法察觉)。然而,大多数时候,它们是不能被忽视的,我们要确保接收者得到正确的信息流。
为了克服信息传输固有的不准确性,已经开发了一些错误检测和纠正的方法。一般来说,这些方法向实际消息引入了一些冗余,这反过来又可用于检测错误,并在某些情况下恢复原始数据。
常见的方法之一是使用CRC(循环冗余校验)功能,这是 一组常用于通过检测由于消息流中的噪声或位丢失而导致的错误来确保数字数据流中的数据完整性的代码。CRC 计算附加到数据流并与消息一起传输的一系列位(通常也称为 CRC)。接收方对消息执行 CRC 函数,并将结果与??接收到的 CRC 码进行比较,以验证消息的完整性。CRC 通常用于许多应用,例如数字通信和计算机数据存储系统。
CRC 通过所传输的消息和多项式除数之间的二进制多项式除法来执行,并且通常使用线性反馈移位
寄存器(LFSR)来实现。LFSR 是一个移位寄存器,其下一个状态是其先前状态和输入位的线性组合。在我们的上下文中,线性运算符是逻辑异或和逻辑与。由于 LFSR 电路的操作是确定性的,并且 CRC 比消息短,因此通常很少有消息映射到每个 CRC 值。精心选择的多项式可确保消息到 CRC 值的均匀分布映射(例如,如果所有消息都映射到相同的 CRC,则不可能检测到消息位中的错误)。
嵌入式系统设计的技巧是以尽可能有效的方式和尽可能小的占用空间来实现该技术。在本文中,我们讨论了 LFSR 和 CRC 的理论和实现的各个方面,并使用
Analog Devices Blackfin
处理器上专门为解决高效 LFSR 实现任务而定义的一系列指令进行说明。我们还提供了一种将实现从内部 LFSR 形式转换为外部 LFSR 形式的方法。
基础知识
CRC 的开发是为了满足错误
检测机制的要求。该代码由一个位字段(具有一定的设定长度)组成,该位字段与消息(通常附加到消息中)一起通过通信介质传输。在接收方,根据接收到的消息计算第二个 CRC,然后与接收到的 CRC 进行比较。如果两个字段不相同,则传输中发生错误(但不知道是消息错误、CRC 错误还是两者都错误)。
为了计算消息的 CRC 代码,我们将问题视为伽罗瓦域 GF(2) 上的多项式代数练习。简而言之,GF(2) 是一个由元素 0 和 1 组成的域,+ 和* 运算符定义为模 2;换句话说,+ 是逻辑异或,* 是逻辑与。
方法对于长度为 k位 的
消息串M和长度为n 位的CRC字段 ,我们定义以下多项式:
M k-1 (x)是k-1 次多项式,其形式为:
M k-1 (x) = m k -1 x k -1 + m k -2 x k -2 +…+ m 0 x 0
G n (x)是n 次 CRC 生成多项式:
G n ( x ) = x n + g n -1 x n -1 +…+ g 0 x 0
C n-1 (x)是计算出的n-1 次 CRC 多项式:
C n -1 ( x ) = c n -1 x n -1 + c n -2 x n -2 +…+ c 0 x 0
CRC 是这样确定的:
C n -1 ( x ) = { M k -1 ( x ) ? x n } mod G n ( x )
模除法 在 GF(2) 上进行模 2。消息字符串的k 位附加了n 位零(这是 等式中的x n项)。这种划分通常使用 LFSR 电路来实现。LFSR 实现恰好有两种规范形式,它们是可以互换的,因为在给定相同的消息和除数多项式的情况下,它们将计算相同的结果。
一种称为外部、I 型 或斐波那契 LFSR 的 形式在反馈路径中具有
异或门,反馈项从相关抽头中采样、相加(模 2),然后反馈到有效位 (lsb) 。
另一种形式称为内部 II 型 或伽罗瓦 LFSR, 采用阶位 (msb) 作为反馈项,通过位于抽头之间的异或门反馈到相关抽头。这种形式更流行,因为用硬件逻辑门实现时它似乎更快。事实上,我们可以看到代数过程和这种 LFSR 除法之间的相似之处。然而,许多实施者并不知道这两种形式的等效性。
内部 CRC LFSR 的实现如图 1 所示。等效的外部 LFSR 的形式如图 2 所示。
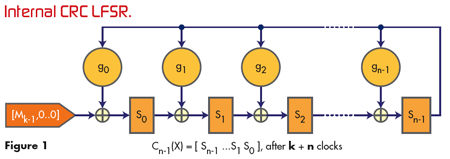
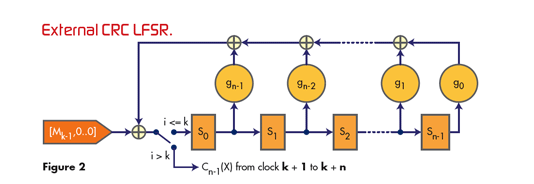
如前所述,这两种电路是等效的,从内部形式转换为外部形式的简单规则是:
1. 在保持LFSR流向相同的情况下,颠倒反馈抽头的顺序;
2. 在前k个 时钟之后,向个抽头 ( S 0 )馈送n 个 零,并读取n 个 输出位(这是所需的 CRC)作为反馈和输入的总和。
在这两种情况下,M 都是从位m k -1开始馈入的。例如,考虑生成多项式G 5 ( x )= x 5 + x 4 + x 2 +1 的两个等效实现,如图 3 和 4 所示。

如果输入端具有相同的位序列,则两个电路生成的 CRC 将相同。


