模拟
滤波器会引入相位失真。
ADC 注入一个无法轻易从所需信息中删除的直流项。请注意,图 1 的 IF 混频器将所需通道的中心频率转换为 DC,其中 ADC 可以注入误差项。该 ADC 偏移可由其构建模块(例如
放大器和比较器)的偏移产生。即使零信号施加到 ADC 时,偏移项也会产生非零数字代码。这对于以极低频率传递信息的系统非常重要。
我们可以弥补接收器 DSP 部分的这些缺陷;然而,更好的解决方案是将 A/D 转换器放在接收器链中的正交混频器之前。如图 2 所示。
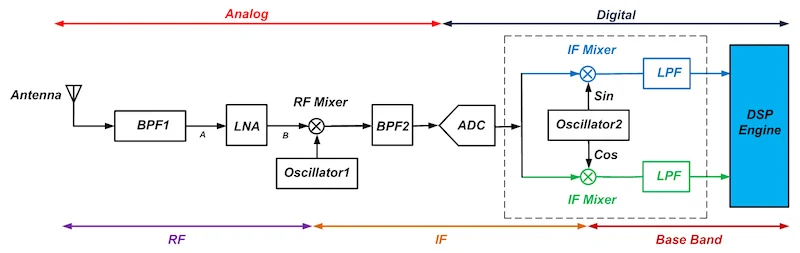
正如您所看到的,现在 A/D 转换发生在中频而不是基带。这意味着 ADC 必须以更高的采样率运行。如图所示,ADC之后的模块都在数字域中操作。例如,图2中
振荡器2的输出实际上是与正弦和余弦信号对应的数字值。为了实现振荡器 2,我们通常使用直接数字合成器(DDS)。第二次下
变频是使用两个数字乘法器执行的,LPF 是数字滤波器。
如上所述,采用图 2 的结构,ADC 将必须以更高的采样率运行。这可能被认为是一个缺点,但 DDC 方法也提供了显着的优点:
现在,中频混频器和低通滤波器都是数字电路。因此,由模拟组件之间的不匹配引起的不平衡相关失真已被消除。
与模拟域不同,我们可以轻松设计线性相位数字滤波器。
在信号通过 IF 混频器之前,数字滤波器可以轻松去除由 ADC 注入的 DC 项( 示例请参见《无线通信和广播中的数字前端》第 12 章)。
请注意,虽然图 2 中的正交混频器和 LPF 位于接收器 DSP 引擎之外,但我们当然可以在系统的 DSP 平台内实现这些模块。此外,在基带 LPF 之后,我们可以显着降低采样率,而不会丢失所需的信息(有关更多信息,请参阅我关于 多速率 DSP 及其在 A/D 转换中的应用的文章 )。因此,我们可以重新绘制图 2 虚线框内的电路,如图 3 所示。该块称为数字下
变频器或 DDC。
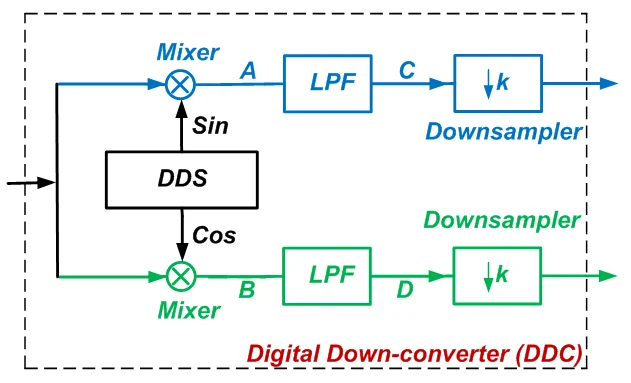
数字下变频
假设经过模数转换后,所需信号的频谱如图 4 所示。

所需信号的中心频率为 110 MHz,带宽为 4 MHz(该图显示了正频率和负频率)。此外,我们假设 ADC 以 440 MSPS(每秒兆样本)的速率生成样本。DDC 将如何处理该输入?
DDC 使用的 DDS 将生成 110 MHz 正弦和余弦信号。每个正弦和余弦函数都会产生 $$\pm 110$$ MHz 的脉冲。由于时域中的乘法对应于频域中的卷积,因此我们将得到图 3 中节点 A 和 B 的频谱,如图 5 所示。兆赫。由于时域中的乘法对应于频域中的卷积,因此我们将得到图 3 中节点 A 和 B 的频谱,如图 5 所示。
±
110

图5
正如您所看到的,$$\pm 110$$ MHz 的频移已将图 4 的蓝色频谱转换为 220 MHz 和 DC。同样,绿色频谱移至 DC 和 -220 MHz。我们能够对节点 A 和 B 使用一张图,因为这两个节点具有相同的幅度特性,并且图 5 仅传达了幅度谱。节点 A 的相位谱将不同于节点 B 的相位谱。 MHz 已将图 4 的蓝色频谱转换为 220 MHz 和 DC。同样,绿色频谱移至 DC 和 -220 MHz。我们能够对节点 A 和 B 使用一张图,因为这两个节点具有相同的幅度特性,并且图 5 仅传达了幅度谱。节点 A 的相位谱将不同于节点 B 的相位谱。
±
110
在图 5 中,请注意,下变频后信号边带在 DC 周围重叠。考虑到这种重叠,我们可以仅使用以 DC 为中心的频谱部分来恢复所需的信息吗?我们可以; 我们使用正交混合,它生成两个相同的幅度谱,但也生成两个不同的相位谱,并且重叠区域的相位谱使我们能够恢复原始信息。由于这种重叠不是问题,因此高于 2 MHz 的频率分量不能提供任何必要的信息,因此我们可以在数字混频器之后放置一个 LPF,以仅保留低于 2 MHz 的频率分量。这种低通滤波在图 3 中描绘为单级滤波器,通常作为两级滤波器实现,如图 6 所示。

图6
级 LPF1 可设计为消除以 220 MHz 为中心的高频分量。为此,我们需要一个通带延伸至约 2 MHz 且阻带从约 218 MHz 开始的 LPF。该滤波操作有时称为对 DDS 创建的图像信号进行滤波。
第二级 LPF2 消除了 2 MHz 至 218 MHz 之间的任何不需要的频率分量。经过 LPF2 后,信号不包含超出预期信息带宽(即 2 MHz)的频率分量,但我们仍然使用 440 MSPS 来表示该信号。因此,我们可以应用下采样概念来降低采样率。




