使用多层感知器进行高级机器学习

到目前为止，我们关注的是单层感知器，它由一个输入层和一个输出层组成。您可能还记得，我们使用术语“单层”是因为此配置仅包括一层计算活动节点，即通过求和然后应用激活函数来修改数据的节点。输入层中的节点只是分发数据。

单层感知器在概念上很简单，训练过程非常简单。不幸的是，它不提供我们复杂的、现实生活中的应用程序所需的功能。我的印象是，解释单层感知器的基本限制的标准方法是使用布尔运算作为说明性示例，这就是我将在本文中采用的方法。

神经网络逻辑门

我们将使用一个极其复杂的微处理器来实现一个神经网络，该神经网络可以完成与由少数晶体管组成的电路相同的事情，这个想法有些幽默。但与此同时，以这种方式思考这个问题强调了单层感知器作为一般分类和函数逼近工具的不足——如果我们的感知器不能复制单个逻辑门的行为，我们知道我们需要找到一个更好的感知器。

让我们回到本系列篇文章中介绍的系统配置。

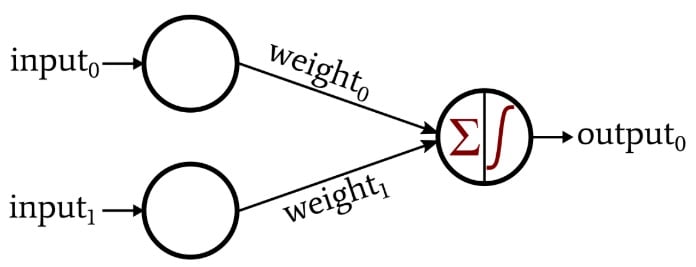
这个感知器的一般形状让我想起了一个逻辑门，事实上，它很快就会变成这样。假设我们使用包含输入向量元素的 0 和 1 的样本来训练该网络，并且仅当两个输入都等于 1 时输出值才等于 1。结果将是一个神经网络，它以类似于与门的电气行为的方式对输入向量进行分类。

该网络输入的维数为 2，因此我们可以轻松地将输入样本绘制成二维图形。假设 input0 对应于水平轴，input1 对应于垂直轴。四种可能的输入组合将排列如下：

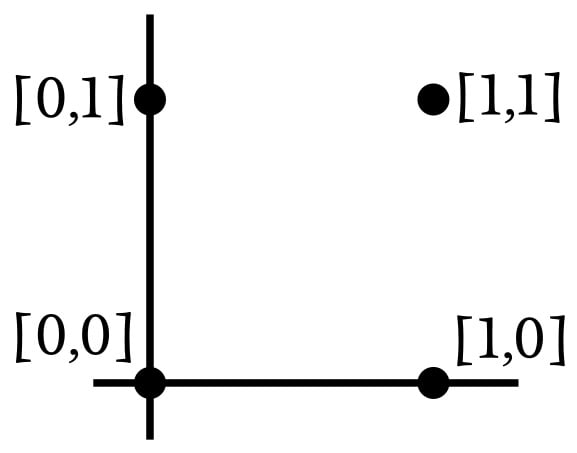
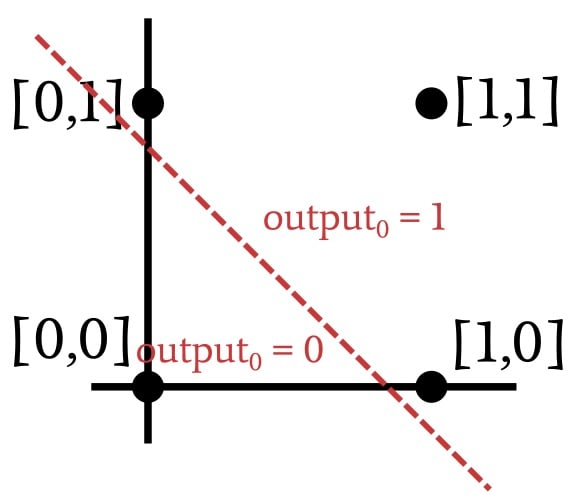
由于我们正在复制 AND 操作，因此网络需要修改其权重，使输入向量 [1,1] 的输出为 1，其他三个输入向量的输出为 0。基于这些信息，让我们将输入空间划分为对应于所需输出分类的部分：

线性可分数据

如上图所示，当我们实现 AND 运算时，可以通过绘制一条直线对绘制的输入向量进行分类。线一侧的所有内容接收到的输出值为 1，而另一侧的所有内容接收到的输出值为零。因此，在 AND 运算的情况下，呈现给网络的数据是线性可分的。OR 操作也是如此：

事实证明，单层感知器只有在数据线性可分的情况下才能解决问题。无论输入样本的维数如何，都是如此。二维情况很容易可视化，因为我们可以绘制点并用一条线将它们分开。为了概括线性可分性的概念，我们必须使用“超平面”这个词而不是“线”。超平面是在n维空间中可以分离数据的几何特征。在二维环境中，超平面是一维特征（即一条线）。在三维环境中，超平面是一个普通的二维平面。在n维环境中，超平面具有 ( n -1) 维。

解决不可线性分离的问题

在训练过程中，单层感知器使用训练样本来确定分类超平面的位置。在找到能够可靠地将数据分成正确的分类类别的超平面后，它就可以采取行动了。然而，如果超平面不存在，感知器将不会找到它。让我们看一个不可线性分离的输入到输出关系的例子：

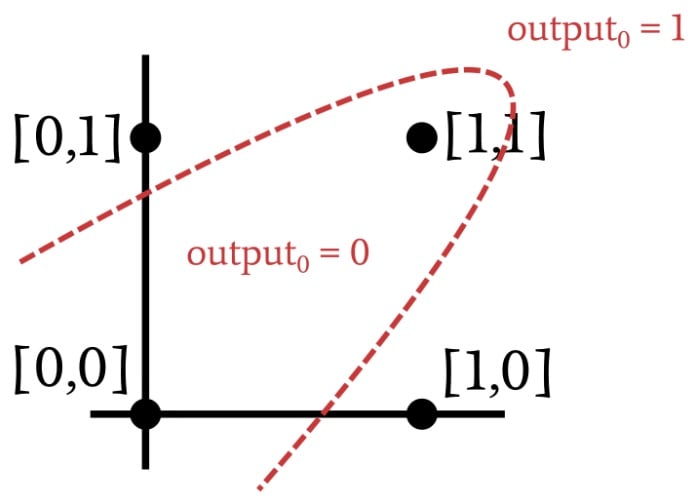
你承认这种关系吗？再看一看，无非是异或运算。您不能用直线分隔 XOR 数据。因此，单层感知器无法实现异或门提供的功能，如果它无法执行异或运算，我们可以放心地假设许多其他（更有趣的）应用程序将超出问题的范围 -解决单层感知器的能力。

幸运的是，我们可以通过简单地增加一层额外的节点来大大提高神经网络解决问题的能力。这将单层感知器变成了多层感知器 (MLP)。正如上一篇文章所提到的，这一层之所以被称为“隐藏”，是因为它与外界没有直接的接口。我想您可以将 MLP 视为众所周知的“黑匣子”，它接受输入数据、执行神秘的数学运算并生成输出数据。隐藏层在那个黑盒子里面。你看不到它，但它就在那里。